scipy库中的odeint函数
scipy.integrate.odeint(func,y0,t,args =(),Dfun = None,col_deriv = 0,full_output = 0,ml = None,mu = None,rtol = None,atol = None,tcrit = None,h0 = 0.0,hmax = 0.0,hmin = 0.0,ixpr = 0,mxstep = 0,mxhnil = 0,mxordn = 12,mxords = 5,printmessg = 0,tfirst = False)
解决一阶ode-s的刚性或非刚性系统的初值问题:
dy/dt = func(y, t, …) [or func(t, y, …)]
主要参量
func callable(y,t,…)或callable(t,y,…)
计算t处y的导数。如果签名是,则必须设置参数 tfirst。callable(t, y, ...)True
y0 数组
y的初始条件(可以是向量)。
t 数组
求解y的时间点序列。初始值点应该是此序列的第一个元素。此序列必须单调增加或单调减少;允许重复的值。
args 元组,可选
传递给函数的额外参数。
例子:
摆锤的重力角在摩擦力作用下的角度θ的二阶微分方程可以写成:
theta’’(t) + btheta’(t) + csin(theta(t)) = 0
其中b和c是正常数,符号(’)表示导数。要使用odeint来求解该方程,我们必须首先将其转换为一阶方程组。通过定义角速度,我们得到系统:omega(t) = theta’(t)
theta'(t) = omega(t)
omega'(t) = -b*omega(t) - c*sin(theta(t))
令y为向量[ θ,ω ]。我们在python中将该系统实现为:
def pend(y, t, b, c):
theta, omega = y
dydt = [omega, -b*omega - c*np.sin(theta)]
return dydt
我们假设常数为b = 0.25和c = 5.0;
b = 0.25
c = 5.0
对于初始条件,我们假设摆是接近垂直的,theta(0) = pi -0.1,并且最初处于静止状态,所以 omega(0) =0。那么初始条件的向量为
y0 = [np.pi - 0.1, 0.0]
我们将以间隔0 <= t <= 10的101个均匀间隔的样本生成一个解。因此,我们的时间数组为:
t = np.linspace(0, 10, 101)
调用odeint以生成解决方案。要将参数b和c传递 给pend,我们odeint使用args 参数使它们能够使用。
from scipy.integrate import odeint
sol = odeint(pend, y0, t, args=(b, c))
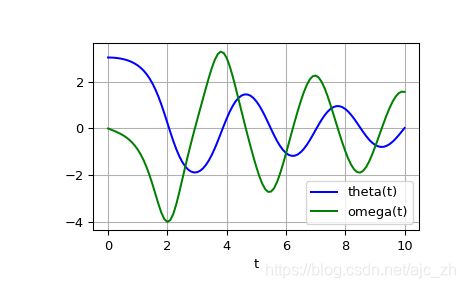
该解决方案是形状为(101,2)的数组。第一列是theta(t),第二列是omega(t)。以下代码绘制了这两个组件。
import matplotlib.pyplot as plt
plt.plot(t, sol[:, 0], 'b', label='theta(t)')
plt.plot(t, sol[:, 1], 'g', label='omega(t)')
plt.legend(loc='best')
plt.xlabel('t')
plt.grid()
plt.show()
参考Scipy.org
https://docs.scipy.org/doc/scipy/reference/index.html
https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html