记scipy中odeint函数用法
记scipy中odeint函数用法
小白艰难自学之路-(一)
odeint介绍
odeint()函数是scipy库中一个数值求解微分方程的函数
odeint()函数需要至少三个变量,第一个是微分方程函数,第二个是微分方程初值,第三个是微分的自变量。
一个一阶微分方程例子
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
def diff(y, x):
return np.array(x)
# 上面定义的函数在odeint里面体现的就是dy/dx = x
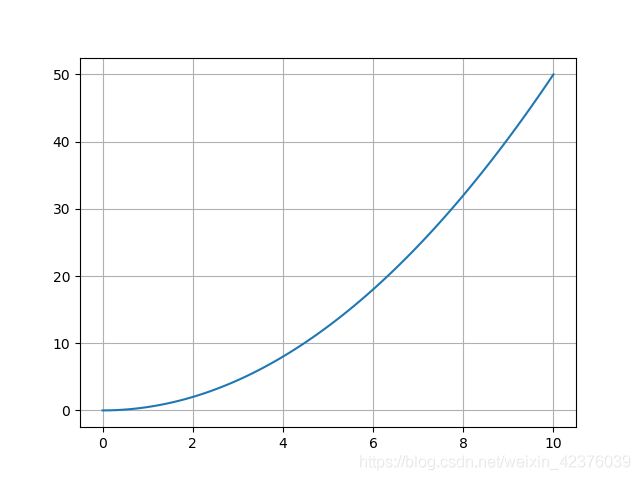
x = np.linspace(0, 10, 100) # 给出x范围
y = odeint(diff, 0, x) # 设初值为0 此时y为一个数组,元素为不同x对应的y值
# 也可以直接y = odeint(lambda y, x: x, 0, x)
plt.plot(x, y[:, 0]) # y数组(矩阵)的第一列,(因为维度相同,plt.plot(x, y)效果相同)
plt.grid()
plt.show()
odeint()函数中第一个变量微分方程的函数中可以定义不止一个一阶微分方程,定义多个一阶微分方程就可以解高阶方程,下面是一个解单摆的例子
d 2 θ d t 2 = − g l θ \frac { \mathrm { d }^2 \theta } { \mathrm { d } t^2 } =- \frac{g}{l} \theta dt2d2θ=−lgθ
将其转化为两个一阶微分方程
d θ d t = ω , d ω d t = − g l θ \frac { \mathrm {d} \theta } { \mathrm {d}t}= \omega, \frac{ \mathrm{d} \omega}{\mathrm{d}t} =- \frac{g}{l} \theta dtdθ=ω,dtdω=−lgθ
g = 9.8
l = 1
def diff2(d_list, t):
omega, theta = d_list
return np.array([-g/l*theta, omega])
t = np.linspace(0, 20, 2000)
result = odeint(diff2, [0, 35/180*np.pi], t)
# 结果是一个两列的矩阵, odeint中第二个是初始单摆角度35度
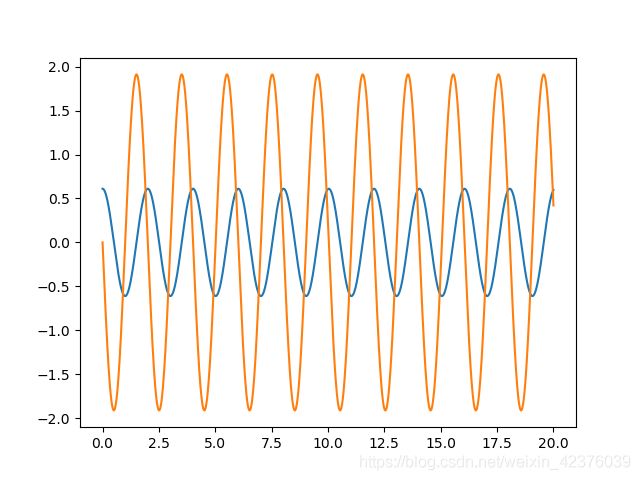
plt.plot(t, result[:, 0]) # 输出omega随时变化曲线
plt.plot(t, result[:, 1]) # 输出theta随时变化曲线,即方程解
plt.show()