python机器学习之降维算法PCA人脸识别中的参数和接口案例,用PCA做噪音过滤

降维算法PCA

一.人脸识别中的components_ 应用

首先导入所需要的库

from sklearn.datasets import fetch_lfw_people#人脸识别数据
from sklearn.decomposition import PCA 
import matplotlib.pyplot as plt
import numpy as np

实例化数据集

faces = fetch_lfw_people(min_faces_per_person=60)#实例化   #每个人需要60张图
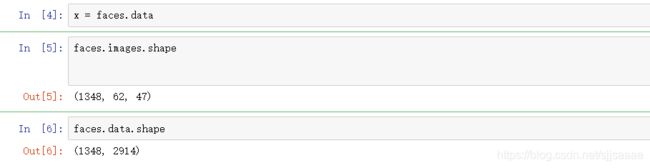
faces.images.shape

运行很慢,需要自动下载fetch_lfw_people,慢慢等待,如果出问题请看–>解决数据问题网页链接

查看数据维度

x = faces.data
faces.images.shape
faces.data.shape

1348 是矩阵中图像的个数
62 是每个图象的特征矩阵的行
47 是每个图像的特征矩阵的列

将原特征矩阵进行可视化
数据本身是图像,和数据本身只是数字,使用的可视化方法不同

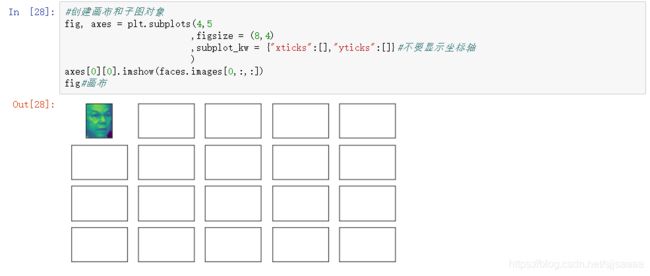
创建画布和子图对象

fig, axes = plt.subplots(4,5
                        ,figsize = (8,4)
                        ,subplot_kw = {
     "xticks":[],"yticks":[]}#不要显示坐标轴
                        )

fig#画布

axes#生成的子图对象

画一个图

axes[0][0].imshow(faces.images[0,:,:])

需要加在画布里面

将数据对象换成一维

axes.flat#降维,变成一维
[*axes.flat]#查看

换成元组

[*enumerate(axes.flat)]#在前面加上一行索引,组成元组

将对象便利到画布里面

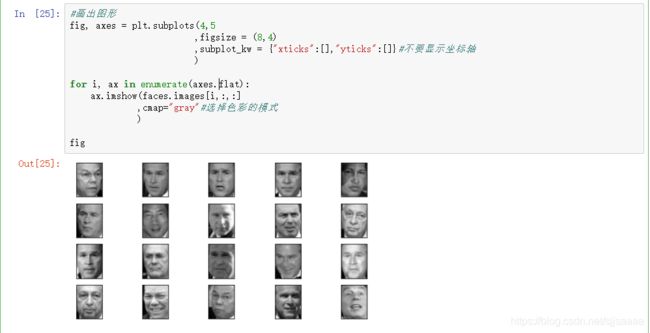
for i, ax in enumerate(axes.flat):
    ax.imshow(faces.images[i,:,:]
             ,cmap="gray"#选择色彩的模式
             )

画出图形

fig, axes = plt.subplots(4,5
                        ,figsize = (8,4)
                        ,subplot_kw = {
     "xticks":[],"yticks":[]}#不要显示坐标轴
                        )

for i, ax in enumerate(axes.flat):
    ax.imshow(faces.images[i,:,:]
             ,cmap="gray"#选择色彩的模式
             )
    
fig

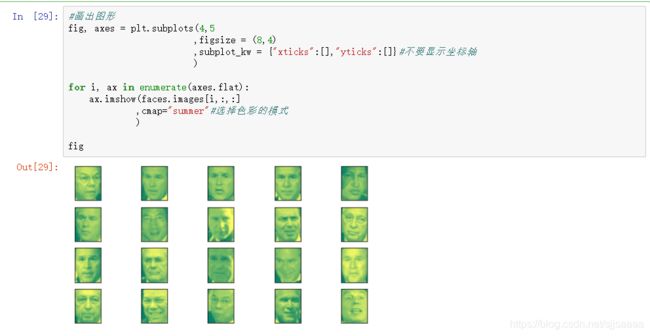
这里附上几个颜色:#颜色[“binary”,“winter”,“afmhot”,“pink”,“summer”,“bone”,“hot”]

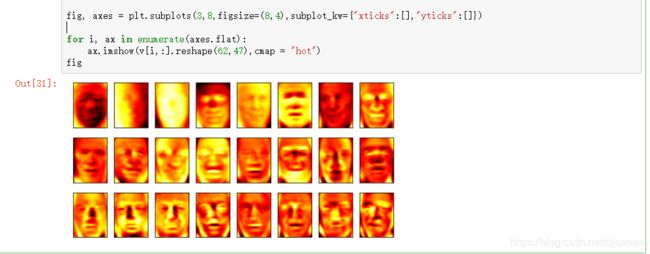
PCA建模降维,降到150维

pca = PCA(150).fit(x)
v = pca.components_  #在映射之前选的特征
v.shape

将新特征空间矩阵可视化

fig, axes = plt.subplots(3,8,figsize=(8,4),subplot_kw={
     "xticks":[],"yticks":[]})

for i, ax in enumerate(axes.flat):
    ax.imshow(v[i,:].reshape(62,47),cmap = "hot")
fig

PCA能够将原始数据集中重要的数据进行聚类

二.重要接口:inverse_transform

用人脸识别 看PCA降维后的信息保存保存量

导入库

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA 
import matplotlib.pyplot as plt
import numpy as np

实例化数据集,探索数据

faces = fetch_lfw_people(min_faces_per_person=60)#实例化   #每个人需要60张图
faces.images.shape
x = faces.data

模型降维,获取降维后的特征矩阵x_dr

pca = PCA(150)#实例化
x_dr = pca.fit_transform(x)#拟合+提取结果
x_dr.shape

将降维后矩阵用 inverse_transform返回原空间

x_inverse = pca.inverse_transform(x_dr)
x_inverse.shape

将特征矩阵x和x_inverse可视化

fig, ax = plt.subplots(2,10,figsize=(10,2.5)
                      ,subplot_kw = {
     "xticks":[],"yticks":[]})

for i in range(10):
    ax[0,i].imshow(faces.images[i,:,:],cmap = "binary_r")
    ax[1,i].imshow(x_inverse[i].reshape(62,47),cmap = "binary_r")
fig

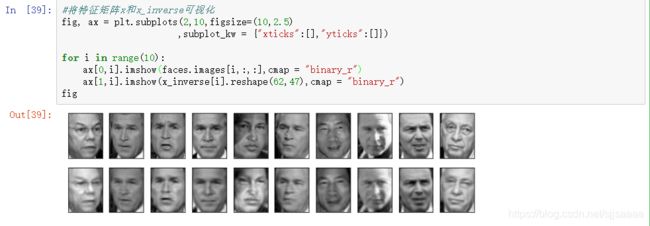
明显看出,这两组数据可视化后,由降维后再通过inverse_transform转换回原维度的数据画出的图像和原数据画的图像大致相似,但是原数据的图像明显更加清洗,这说明inverse_transform并没有实现数据的完全逆转

三.用PCA做噪音过滤

降维的目的之一就是希望抛弃掉对模型带来负面影响的特征,利用inverse_transform的这个性质,我们能够实现噪音过滤.

导入库

from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

导入数据,探索数据

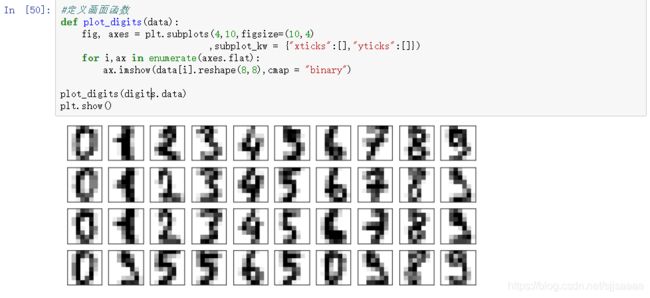
digits = load_digits()
digits.data.shape

定义画面函数

def plot_digits(data):
    fig, axes = plt.subplots(4,10,figsize=(10,4)
                            ,subplot_kw = {
     "xticks":[],"yticks":[]})
    for i,ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8,8),cmap = "binary")
        
plot_digits(digits.data)
plt.show()

为数据加上噪音

rng = np.random.RandomState(42)
noisy = rng.normal(digits.data,2)
plot_digits(noisy)
plt.show()

在指定的数据集中,随机抽取服从正态分布的数据,两个参数,分别是指定的数据集,和抽取出来的正态分布的方差.

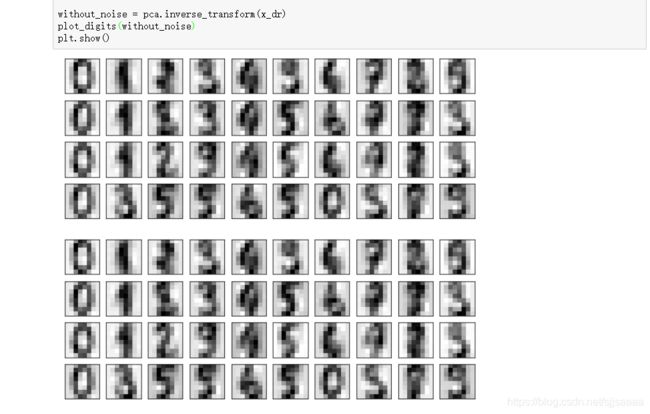
使用PCA降维

pca = PCA(0.5,svd_solver="full").fit(noisy)
x_dr = pca.transform(noisy)
x_dr.shape

逆转降维结果,实现降噪

without_noise = pca.inverse_transform(x_dr)
plot_digits(without_noise)
plt.show()

对比发现,降维后的效果比添加噪音时代的效果好一些.
所以PCA可以可以实现降噪.