在前面的文章中讲过,很多模型的假设条件都是数据是服从正态分布的。这篇文章主要讲讲如何判断数据是否符合正态分布。主要分为两种方法:描述统计方法和统计检验方法。
01.描述统计方法
描述统计就是用描述的数字或图表来判断数据是否符合正态分布。常用的方法有Q-Q图、P-P图、直方图、茎叶图。
1.1 Q-Q图
此Q-Q非用于聊天的QQ,Q是quantile的缩写,即分位数。分位数就是将数据从小到大排序,然后切成100份,看不同位置处的值。比如中位数,就是中间位置的值。
Q-Q图的x轴为分位数,y轴为分位数对应的样本值。x-y是散点图的形式,通过散点图可以拟合出一条直线,如果这条直线是从左下角到右上角的一条直线,则可以判断数据符合正态分布,否则则不可以。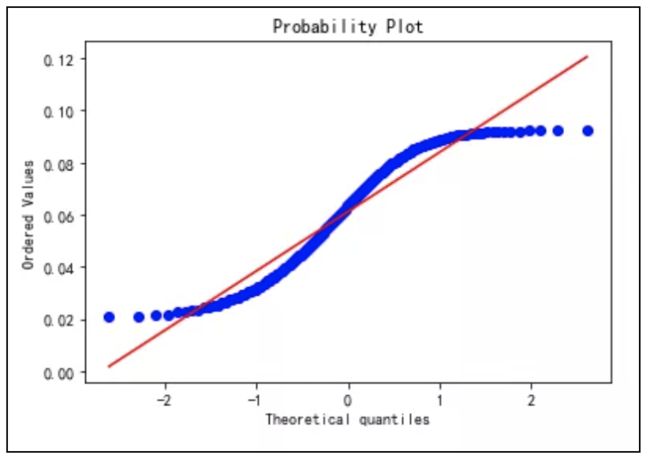
拟合出来的这条直线和正态分布之间有什么关系呢?为什么可以根据这条直线来判断数据是否符合正态分布呢。
我们先来想一下正态分布的特征,正态分布的x轴为样本值,从左到右x是逐渐增大的,y轴是每个样本值对应的出现的概率。概率值先上升后下降,且在中间位置达到最高。
可以把Q-Q图中的y轴理解成正态分布中的x轴,如果拟合出来的直线是45度,可以保证中位数两边的数值分布是一样的,即正态分布中基于中位数左右对称。
在Python中可以使用如下代码来绘制Q-Q图:
from scipy import stats
fig = plt.figure()
res = stats.probplot(x, plot=plt)
plt.show()
与Q-Q图类似的是P-P图,两者的区别是前者的y轴是具体的分位数对应的样本值,而后者是累计概率。
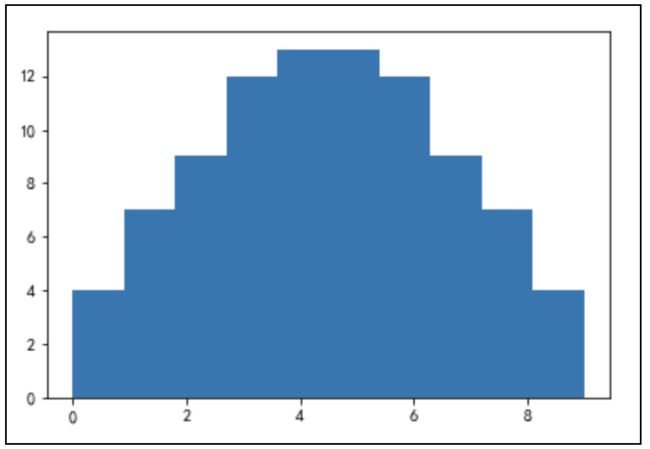
1.2 直方图
直方图分为两种,一种是频率分布直方图,一种是频数分布直方图。频数就是样本值出现的次数,频率是某个值出现的次数与所有样本值出现总次数的比值。
在Python中我们可以使用如下代码来绘制频数分布直方图:
import matplotlib.pyplot as plt
plt.hist(x,bins = 10)
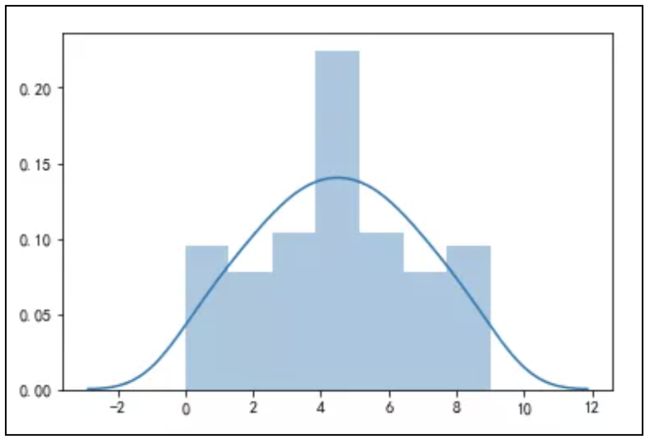
可以使用如下代码来绘制频率分布直方图:
import seaborn as sns
sns.distplot(x)
与直方图类似的还有茎叶图,茎叶图是类似于表格形式去表示每个值出现的频次。
02.统计检验方法
讲完了描述统计的方法,我们来看一下统计检验的方法。统计检验的方法主要有SW检验、KS检验、AD检验、W检验。
SW检验中的S就是偏度,W就是峰度,峰度和偏度与正态的关系我们在前面的文章有讲过。
2.1 KS检验
KS检验是基于样本累积分布函数来进行判断的。可以用于判断某个样本集是否符合某个已知分布,也可以用于检验两个样本之间的显著性差异。
如果是判断某个样本是否符合某个已知分布,比如正态分布,则需要先计算出标准正态分布的累计分布函数,然后在计算样本集的累计分布函数。两个函数之间在不同的取值处会有不同的差值。我们只需要找出来差值最大的那个点D。然后基于样本集的样本数和显著性水平找到差值边界值(类似于t检验的边界值)。判断边界值和D的关系,如果D小于边界值,则可以认为样本的分布符合已知分布,否则不可以。
PDF( probability density function):概率密度函数。
CDF( cumulative distribution function):累积分布函数,是概率密度函数的积分。
在Python中有现成的包可以直接用于KS检验:
from scipy.stats import kstest
kstest(x,cdf = "norm")
x表示待检验的样本集,cdf用来指明要判断的已知分布类型,有:‘norm’,’expon’,’logistic’,’gumbel’,’gumbel_l’, gumbel_r’,
‘extreme1’值可以选,其中norm表示正态分布检验。
kstest会返回两个值:D和对应的p_value值。
2.2 AD检验
AD检验是在KS基础上进行改造的,KS检验只考虑了两个分布之间差值最大的那个点,但是这容易受异常值的影响。AD检验考虑了分布上每个点处的差值。
在Python中可以用如下代码:
from scipy.stats import anderson
anderson(x, dist='norm')
x为待检验的样本集,dist用来指明已知分布的类型。可选值与ks检验中可选值一致。
上面代码会返回三个结果: 第一个为统计值,第二个为评判值,第三个为每个评判值对应的显著性水平
AD检验和anderson有啥关系呢?anderson发明了AD检验。
2.3 W检验
W检验(Shapiro-Wilk的简称)是基于两个分布的相关性来进行判断,会得出一个类似于皮尔逊相关系数的值。值越大,说明两个分布越相关,越符合某个分布。
在Python中的实现代码如下:
from scipy.stats import shapiro
shapiro(x)
上面的代码会返回两个结果:W值和其对应的p_value。
shapiro是专门用于正态性检验的,所以不需要指明分布类型。且 shapiro 不适合做样本数>5000的正态性检验。
03.非正态数据的处理办法
一般数据不是正态就是偏态,如果偏态不严重可以对数据取平方根来进行转换。如果偏态很严重,则可以对数据进行对数转换。