机器学习笔记——乳腺癌鸢尾花分类问题详解（没有直接调包）

前言

前面一段时间是真的忙，10月20几号才开始准备软考（好家伙，我以为是12月份考试，结果是11月7号考试），半个月的时间学完差不多大学四年的课程，每天除了上课就是盯着软考书看和刷软考通了，但是我们俱乐部每周还是会安排时间给我们培训机器学习、深度学习方面的知识，中间一个月没有写博客了，很多学到的知识当时虽然是搞明白了，由于事后没有总结和回顾，好多都慢慢遗忘了，这也就是为什么我要坚持写博客的原因，虽说有的时候一两个月都不见得更新一次，但是只要学习了新的我感兴趣的技术我都会写下来。好记性不如烂笔头，建议大家也有一个好的习惯，不说每个人都要写个博客，起码事后能翻一翻看一看回顾一下，这对你记住乃至于以后运用这个知识是非常有帮助的。

好了，废话不多说。这篇文章的主要内容是讲机器学习中的分类问题，目前我学的比较基础，没有用到一些高深的算法，相信有一定编程和数学基础的同学是都能看懂的。
机器学习概述和波士顿房价问题这个回归问题模型可以看我前面写的博客：机器学习学习笔记——以波士顿房价问题为例

二分类问题——乳腺癌分类

问题概述及数据导入

我们一般接触到的分类问题是属于二分类，非此即彼。像乳腺癌分类问题就是一个二分类问题，给定一组数据判断她是否会得乳腺癌。

对于乳腺癌分类问题，首先我们还是从sk-learn中导入数据集，可以发现影响是否患有乳腺癌的因素有30个，整个数据集中有569条数据。

模型分析

首先对于乳腺癌分类问题来说，我们的变量有30种，不再是之前讲道德线性回归问题当中的一种，所以我们再用线性函数去模拟数据是行不通的，当有多个变量时，我们可以选择将直线变弯的方式来拟合我们的数据，即将线性函数变弯曲，通过某个函数加上线性函数的方式拟合数据，这里就是我们说到的激活函数。激活函数的目的就是将线性函数引入非线性特征，使得我们得到的模型能够拟合任意的非线性函数。
从上面的数据导入部分可以看到，我们的结果y值是0或1，此时我们就会想，有没有一个函数能将我们一堆x的值映射到0-1这个区间之内呢？为此我们引入sigmoid()函数：


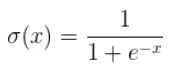
sigmoid()函数的代码表示：

def sigmoid(x):
    return 1 / (1 + np.exp(-1*x))

sigmoid()函数能将我们的输入值映射到0-1这个区间内，这样的话我们通过输出值来判断他是0还是1，比如我们给定一个规则：如果输出的值是在[0,0.5]那么代表判断结果是0，输出的值是在(0.5,1]那么代表判断结果是1。这样我们就将一个分类问题变成了一个形式上的回归问题，便于理解判断。
有了以上的分析基础，我们可以简单的得到基于这个二分类问题的模型估计函数：
估计函数：$$\hat{y}=sigmoid(WX+b)$$
损失函数：$$Loss=-(y\log \hat{y}+(1-y)\log (1-\hat{y}))$$
求偏导：$$\frac{\delta Loss}{\delta W}=\frac{\delta Loss}{\delta \hat{y}}\frac{\delta \hat{y}}{\delta sigmoid}\frac{\delta sigmoid}{\delta W}$$

具体代码

# 导入各种库
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
import numpy.random as rd
data = load_breast_cancer()
print(data['feature_names'])

X, y = data['data'], data['target']
# x是569*30
test_num = 100
# 划分训练集和测试集
X_train, X_test = X[test_num:], X[:test_num]
y_train, y_test = y[test_num:], y[:test_num]
learning_rate = 0.0000001
epoch = 20000
min_loss = float('inf')
best_w0, best_w1 = 0, 0
# sigmoid函数
def sigmoid(x):
    return 1 / (1 + np.exp(-1*x))
# 损失函数
def cross_entropy(y, y_hat):
    return -1 * (y * np.log(y_hat) + (1-y) * np.log(1-y_hat))

# mean()函数功能：求取均值
# axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
# axis =1 ：压缩列，对各行求均值，返回 m *1 矩阵
# axis 不设置值，对 m*n 个数求均值，返回一个实数
mean_x = np.mean(X_train, axis=0)
# axis=0计算每一列的标准差
std_x = np.std(X_train, axis=0)
# 对x进行这种处理之后得到的值更普遍具有代表性
X_train = (X_train - mean_x) / std_x
# 返回来一个给定形状和类型的用0填充的数组
w0, w1 = np.zeros(1), rd.normal(size=(30,)) * 0.0001
# print(np.dot(X, w1) + w0)
for e in range(epoch):
    # 计算预测的y值，dot表示求两个矩阵的乘积
    y_hat = sigmoid(np.dot(X_train, w1) + w0)  # (569, )
    # 总的loss值
    loss = np.mean(cross_entropy(y_train, y_hat))
    # d_w0是线性函数截距之差
    d_w0 = np.mean(y_hat - y_train)
    d_w1 = np.dot(X_train.T, (y_hat - y_train))

    w0 = w0 + (-1) * d_w0 * learning_rate
    w1 = w1 + (-1) * d_w1 * learning_rate

    if loss < min_loss:
        min_loss = loss
        best_w0, best_w1 = w0, w1
        print("Loss updated to {} at the {}th epoch.".format(loss, e))

plt.scatter([i for i in range(y_test.shape[0])], y_test)
plt.show()
mean_x_test = np.mean(X_test, axis=0)
std_x_test = np.std(X_test, axis=0)
X_test = (X_test - mean_x_test) / std_x_test
y_hat_test = sigmoid(np.dot(X_test, best_w1) + best_w0) > 0.5
plt.scatter([i for i in range(y_test.shape[0])], y_hat_test)
plt.show()

结果loss值：

代码的注释写的很清楚了，这里我就不再赘述了。

三分类问题——鸢尾花分类

问题概述及数据导入

首先我们来了解鸢尾花分类问题的数据集：


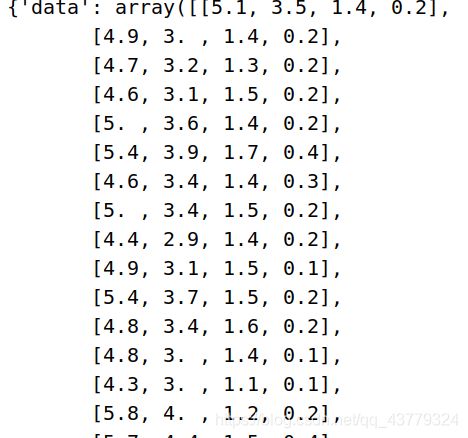
data域是一个150x4的二维数组，target域则是150x1的数组，也就是说我们的鸢尾花数据集有四个变量分别是花萼长、花萼宽、花瓣长、花瓣宽，得到的target是表示这个鸢尾花属于哪一类，数据上共有0、1、2这三类。三分类问题不同于二分类，sigmoid()只能将值映射到0-1，无法将得到的值分成三类。为此我们有softmax()这个激活函数：

softmax()函数的值域是[0,1]，输出是概率值,所以加和为1。用指数的形式是为了使大的值更大，同时也为了求导方便。
softmax()函数代码表示：

def softmax(x):
	return np.exp(x) / np.sum(np.exp(x))

模型分析

首先我们的x是150x4的数据集，y是150x1的数据集，但是我们可以把y变成150x3，这样的好处是我们不再是0、1、2表示三个分类了，而仍然用0和1表示，我们的表示方法是用[1,0,0]表示第一类、[0,1,0]表示第二类、[0,0,1]表示第三类。这样的话我们就可以将x的数据映射到150x3的矩阵上，这里的3就是有三类，我们得到的值分别表示每一类的概率，哪一组哪个位置上的概率值最大，那么就把他归为这一类。x是150x4的矩阵，将y变成150x3的矩阵，我们总体上还是用softmax函数加上一个线性函数这样来模拟，那么线性函数的参数w就要是一个4x3的矩阵，这样才能乘出来是一个150x3的矩阵。

具体代码

from sklearn.datasets import load_iris  # 导入鸢尾花数据集
import numpy as np

iris = load_iris()  # 载入数据集

X, y = iris.data, iris.target


# 将y值转化为向量
def create_y_labels(y):
    new_y = []
    for sample in y:
        if sample == 0:
            new_y.append([1, 0, 0])
        elif sample == 1:
            new_y.append([0, 1, 0])
        else:
            new_y.append([0, 0, 1])
    return np.array(new_y)
y = create_y_labels(y)
def softmax(x):
    return np.exp(x) / np.tile(np.sum(np.exp(x), axis=1).reshape(150, 1), 3)
def cross_entropy(y, y_hat):
    return -1 * np.sum(y * np.log(y_hat))

epoch = 50000
learning_rate = 0.0001
# 通过本函数可以返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)，不包括1。
# 返回的是一个4×3的矩阵，矩阵中每个元素的值在（0,1）
W, b = np.random.rand(4, 3), 0
loss_items = []
min_loss = float('inf')
for e in range(epoch):
    # np.dot()函数用于求两个矩阵的乘积
    y_hat = softmax(np.dot(X, W) + b)  # x是150×4的矩阵，得到的y_hat是150*3的矩阵
    loss = np.mean(cross_entropy(y, y_hat))

    loss_c = y_hat - y
    d_b = np.mean(loss_c)
    #     print('db: {}'.format(d_b.shape))
    d_w = np.dot(X.T, loss_c)  # 4， 3
    #     print('dw: {}'.format(d_w.shape))

    W = W + (-1) * d_w * learning_rate
    b = b + (-1) * d_b * learning_rate
    loss_items.append(loss)
    if loss < min_loss:
        min_loss = loss
        best_W, best_b = W, b
        print("Loss updated to {} at the {}th epoch.".format(loss, e))
yy_hat = softmax(np.dot(X, W) + b)
print(yy_hat)

# 用于找到二维数组中每一行元素的最大值索引并输出
idx = np.argmax(yy_hat, axis=1)
pro = np.amax(yy_hat, axis=1)
print(idx)
import matplotlib.pyplot as plt
flag = 0
for i in range(150):
    if idx[i] == iris.target[i]:
        flag += 1

print(flag)
print("预测率：", flag/150)

plt.plot(loss_items)
plt.show()

以上就是整个分类代码的具体实现，中间主体部分是用来训练参数用的，得到一个较好的w，b值之后带入进行分类。

最后我们可以看到预测率有96.7%，还是比较好的。

后记

算是入门了机器学习这个头秃的家伙，没有点好的高数线代基础学的真的是脑壳大（猛男落泪）。想想就后悔当初上课没有好好听。我会努力的，冲冲冲！！！