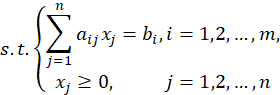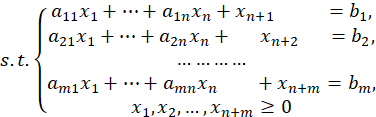最优化课程设计——单纯形法

 

       单纯形法的基本原理及实践案例分析应用

                           摘  要 

      单纯形法是解决线性规划问题的一个有效算法。同时无约束优化的单纯形法可利用对简单几何图形各顶点的目标函数值进行比较，逐步以目标函数值较小的顶点取代目标数值最大的顶点，从而进行求优。本文将从线性规划的数学模型开始，接着介绍单纯形法解决线性规划问题的过程，再介绍无约束优化的单纯形法的原理及步骤，最后利用python、matlab基于实例对单纯形法进行实现。

关键词：线性规划；可行基；无约束最优化；

                                                         

---

                              目录

单纯形法的基本原理及实践案例分析应用

                   摘  要 

第一章 线性规划的一般形式

第二章 单纯形法求解线性规划问题

第三章 无约束最优化的单纯形法

第四章 单纯形法求解线性规划问题的matlab及python实现

第五章 无约束最优化单纯形法的matlab实现 

参考文献

---

第一章 线性规划的一般形式

1.1 线性规划的数学模型

满足以下三个条件的数学模型称为线性规划数学模型：

（1）每一个问题都用一组决策变量表示某一方案；每一组值就代表一个具体方案。

（2）有一个目标函数，可用决策变量的线性函数来表示，按问题的不同，要求目标函数实现最大化或最小化。

（3）有一组约束条件，可用一组线性等式或不等式来表示。

线性规划问题的一般形式为

                                                   

                                                     

这里目标函数中的系数叫做目标函数系数或价值系数，约束条件中的常数叫做资源系数，约束条件中的系数叫做约束系数或技术系数。

1.2 线性规划问题的标准形式

所谓线性规划问题的标准形式，是指目标函数的要求最小，所有约束条件都是等式约束，且所有决策定量都是非负的，即

                                                  

                                                    

或简写为

                                                  

                                                     

线性规划问题的矩阵表示为

                                                 

                                                    

其中,。任意的线性规划模型都可以转化为标准形式。

 

第二章 单纯形法求解线性规划问题

2.1单纯形法的计算步骤

单纯形法是求解线性规划问题的迭代算法。

单纯形法的基本思路是：从可行域中某个基可行解（一个顶点）开始，转换到另一个基可行解（顶点），直到目标函数达到最优时，基可行解即为最优解。单纯形法基本过程如图：

为方便计算，通常借助于单纯形表来计算。单纯形表中列中填入基变量；列填入基变量的价值系数；b列中填入约束方程组右端的常数；θj列的数字是在确定换入变量后，按规则计算填入；最后一行称为检验数行，对应各非基变量的检验数是。

单纯形法的计算步骤：

（1）找出初始可行基，确定初始基可行解，建立初始单纯形表。

（2）检验各非基变量的检验数。若所有的,则已得到最优解，停止计算。否则转入下一步。

（3）在中，若所有,则此问题无最优解，停止计算。否则转入下一步。

（4）以为主元素进行迭代（用高斯消元法），把所对应的列向量

                                                      

将列中的换成得到新的单纯形表，重复步骤（2）——步骤（5），直到终止。

 若目标函数要求实现最大化，一方面可将最大化转换为最小化，另一方面也可在上述计算步骤中将判定最优解的改为，将换入变量的条件改为。

2.2初始可行基的确定

2.2.1 初始可行基的确定

（1）若线性规划问题是

                                                    

                                                   

则从中一般能直接观察到存在一个初始可行基 

                                                   

  （3）对所有约束条件“”形式的不等式及等式约束情况，若存在单位矩阵时，可采用人工变量，即对不等式约束减去一个非负的剩余变量后，再加入一个非负的人工变量；对等式约束再加入一个非负的人工变量，总可以得到一个单位矩阵作为初始可行基。            

2.2.2 大M法

在约束条件中增加入工变量，人工变量再目标函数中的简直系数为

在这里插入图片描述M，M为一个很大的正数。在迭代过程中，将人工变量从基变量中逐个换出，如果在最终表中当所有检验数时，基变量中不再含有非零的人工变量，这表示原问题有解，否则无可行解。

2.2.3 两阶段法

两阶段法是把线性规划问题的求解过程分为两个阶段:

第一阶段,给原问题加入人工变量，构造仅含价值系数为1的人工变量的目标函数且要求实现最小化，其约束条件与原问题相同,即

                                              

                                            

然后用单纯形法求解上述问题，若得到，这说明原问题存在基可行解，可进入第二阶段计算，否则原问题无可行解，停止计算。

第二阶段,将第一阶段计算得到的最终表，除去人工变量,将目标函数行的系数换为原问题的目标函数系数，作为第二阶段计算的初始单纯形表进行计算。

        

第三章 无约束最优化的单纯形法

3.1 无约束最优化

多维无约束最优化问题

                                               

其中这个问题的求解是指，在中找一点，使得对于任意的都有

                                            

成立。点就是问题的全局最优点。

       无约束优化方法是优化技术中极为重要和基本的内容之一。它不仅可以直接用来求解无约束优化问题，而且很多约束优化问题也常将其转化为无约束优化问题，然后用无约束优化方法来求解.另外，有些无约束优化方法只需略加处理，即可用于求解约束优化问题.

       无约束优化理论发展较早，比较成熟，方法也很多,新的方法还在陆续出现.把这些方法归纳起来可以分成两大类:-类是仅用计算函数值所得到的信息来确定搜索方向,通常称它为直接搜索法，简称为直接法,另一类需要计算函数的一阶或二阶导数值所得到的信息来确定搜索方向，这一类方法称为间接法(或解析法):直接法不涉及导数和Hesse矩阵,适应性强,但收敛速度一般较慢;间接法收敛速度一般较快,但需计算梯度,甚至需要计算Hesse矩阵:一般的经验是，在可能求得目标函数导数的情况下还是尽可能使用间接方法;相反,在不可能求得目标函数的导数或根本不存在导数的情况下，当然就应该使用直接法。

3.2单纯形法

      单纯形法是利用对简单几何图形各顶点的目标函数值作相互比较,在连续改变几何图形的过程中，逐步以目标函数值较小的顶点取代目标函数值最大的顶点，从而进行求优的一种方法,属于直接法之一。

3.2.1 单纯形法的基本原理

      以求二元函数的极小点为例，说明单纯形法形成的原理。设二元函数在平面上取不在同一条直线上的三个点，并以它们为顶点构成一单纯形——三角形。算出各顶点的函数值，比较其大小，现假定比较后有

                                            

这说明点最差，点最好，点次差。为了寻找极小点，一般来说应向最差点的反对称方向进行搜索。以记为的中点，在的延长线上取点，使称为关于的反射点。      

 

算出的函数值，可能出现以下几种情形：

（1）

这说明搜索方向正确，可进一步扩大效果，继续沿向前搜索，也就是向前扩张。这时取

                                        

其中为扩张因子，一般取

如果,说明扩张有利，就可以点代替点构成新的单纯形。如果，说明扩张不利，舍序，任以代替构成新的单纯形。

（2）

这说明搜索方向正确，但无须扩张，以代替构成新的单纯形。

（3）

这表示点走的太远，应缩回一些。若以表示压缩因子，则有

                                       

常取为0.5以代替构成新的单纯形

（4）

这时应压缩更多一些，将新点压缩至至之间，令

                                    

以上说明，不管哪种情况，我们都可以得到一个新的单纯形，其中至少有一顶点的函数值比原单纯形为小。如此继续，直至满足收敛终止准则。

    在n维情况下，一个单纯形含有n+1个顶点，计算工作量较大，但原理和上述二维情况相同。

3.2.2 单纯形法的迭代步骤

已知设为n维变量，目标函数为，终止限为

（1）构成初始单纯形。

在n维空间中选初始点（离最优点越近越好），从出发，沿各坐标方向步长移动得个顶点。这样选择顶点可保证向量组

                                     

线性无关。否则，就会使搜索范围局限在较低维的空间内，有可能找不到极小点。当然在各坐标方向可以移动不同的距离。

步长t的范围可取0.5~15.0，开始常取，接近最优点时要减小。

（2）计算各顶点的函数值

                                      

比较各函数值的大小，确定是最好点、最差点和此差点，即

                                     

                                    

                                    

（3）计算之外各点的“重心”

                                    

求出反射点

                                   

（4）当时，需要扩张。令

                                

如果,则以代替形成一新单纯形；否则，以代替构成新单纯形。然后转（8）

（5）当时，以代替构成新单纯形，然后转（8）。

（6）当时,则需要收缩。即令

                                     

以代替得新单纯形，并转（8）

（7）当时，令

                                     

如果，则将单纯形缩边，可将向量的长度缩小一半，即

                                      

这样可得一新单纯形。否则就以代替得新单纯形。然后转（8）

（8）收敛性检验

每次迭代得到新单纯性后，即应进行收敛性检验，如满足收敛指标，则迭代停止，即为所求得近似解。否则，继续进行迭代计算。通常所用的收敛准则是

                                         

或

                                       

式子中和为预先给定得允许误差。

 

第四章 单纯形法求解线性规划问题的matlab及python实现

4.1 单纯形法求解线性规划问题的matlab实现

线性回归问题为

                                       

                                        

Matlab程序：

function [x,f,it]=linp(A,b,c) %输出x为最优解，f为最优值，it为迭代次数。
b=b(:);%变为列向量
it=0;
[m,n]=size(A);
x=zeros(1,n+length(b));
A=[A eye(length(b)) b]; %化为标准型，A b合一块
c=[c zeros(1,length(b)+1)]; %同上
 while ~all(c(1:length(c)-1)>=0) %并非所有的c中前length（c）-1个元素都大于等于零时进入循环
 d=find(c<0);%d(1)-------第一个负数元素列坐标
 e=find(A(:,d(1))>0);% e包含的d（1）列中正元素的行坐标
 g=[];
 for ii=1:length(e)
 g=[g A(e(ii),n+length(b)+1)/A(e(ii),d(1))];
 end
 h=find(g==min(g));%选择离基变量
 p=A(e(h),d(1));
 for ii=1:n+length(b)+1
 A(e(h),ii)=A(e(h),ii)/p;%离基变量 A(e(h),d(1)),对该行进行操作
 end
 j=-c(d(1))/A(e(h),d(1));
 for ii=1:n+length(b)+1
     c(ii)=j*A(e(h),ii)+c(ii);%%%%%对c操作
 end
 for ii=[1:e(h)-1,e(h)+1:m]
     j=-A(ii,d(1))/A(e(h),d(1));
     for kk=1:n+length(b)+1
     A(ii,kk)=j*A(e(h),kk)+A(ii,kk);
     end    
 end%%%%%%%%%%%%截止，对A的操作完成
 it=it+1;
 end
 o=[];
 for ii=1:n
     if all(A(:,ii)>=0)&&sum(A(:,ii))==1
     o=[o ii];
     end %x解的列坐标
 end
 for ii=1:length(o)
     for kk=1:m  %x解的行坐标
         if A(kk,o(ii))==1
             x(o(ii))=A(kk,n+length(b)+1); %对x解进行整理
         end
     end
 end  
 x=x(:);
 f=-c(n+length(b)+1);
end

目标函数： 

 实验结果：

>> A=[-1 1;1 2;3 1];
>> b=[2 10 15];
>> c=[-2 -3];
>> [x,f,it]=linp(A,b,c)

x =

     4
     3
     0
     0
     0


f =

   -17


it =

     2

>> 

4.2 单纯形法求解线性规划问题的python实现

线性回归问题为：

                                              

                                              

Python程序：

# coding=utf-8
# 单纯形法的实现，只支持最简单的实现方法
# 且我们假设约束矩阵A的最后m列是可逆的
# 这样就必须满足A是行满秩的（m*n的矩阵）

import numpy as np


class Simplex(object):
    def __init__(self, c, A, b):
        # 形式 minf(x)=c.Tx
        # s.t. Ax=b
        self.c = c
        self.A = A
        self.b = b

    def run(self):
        c_shape = self.c.shape
        A_shape = self.A.shape
        b_shape = self.b.shape
        assert c_shape[0] == A_shape[1], "Not Aligned A with C shape"
        assert b_shape[0] == A_shape[0], "Not Aligned A with b shape"

        # 找到初始的B，N等值
        end_index = A_shape[1] - A_shape[0]
        N = self.A[:, 0:end_index]
        N_columns = np.arange(0, end_index)
        c_N = self.c[N_columns, :]
        # 第一个B必须是可逆的矩阵，其实这里应该用算法寻找，但此处省略
        B = self.A[:, end_index:]
        B_columns = np.arange(end_index, A_shape[1])
        c_B = self.c[B_columns, :]

        steps = 0
        while True:
            steps += 1
            print("Steps is {}".format(steps))
            is_optim, B_columns, N_columns = self.main_simplex(B, N, c_B, c_N, self.b, B_columns, N_columns)
            if is_optim:
                break
            else:
                B = self.A[:, B_columns]
                N = self.A[:, N_columns]
                c_B = self.c[B_columns, :]
                c_N = self.c[N_columns, :]

    def main_simplex(self, B, N, c_B, c_N, b, B_columns, N_columns):
        B_inverse = np.linalg.inv(B)
        P = (c_N.T - np.matmul(np.matmul(c_B.T, B_inverse), N)).flatten()
        if P.min() >= 0:
            is_optim = True
            print("Reach Optimization.")
            print("B_columns is {}".format(B_columns))
            print("N_columns is {}".format(sorted(N_columns)))
            best_solution_point = np.matmul(B_inverse, b)
            print("Best Solution Point is {}".format(best_solution_point.flatten()))
            print("Best Value is {}".format(np.matmul(c_B.T, best_solution_point).flatten()[0]))
            print("\n")
            return is_optim, B_columns, N_columns
        else:
            # 入基
            N_i_in = np.argmin(P)
            N_i = N[:, N_i_in].reshape(-1, 1)
            # By=Ni， 求出基
            y = np.matmul(B_inverse, N_i)
            x_B = np.matmul(B_inverse, b)
            N_i_out = self.find_out_base(y, x_B)
            tmp = N_columns[N_i_in]
            N_columns[N_i_in] = B_columns[N_i_out]
            B_columns[N_i_out] = tmp
            is_optim = False

            print("Not Reach Optimization")
            print("In Base is {}".format(tmp))
            print("Out Base is {}".format(N_columns[N_i_in]))   # 此时已经被换过去了
            print("B_columns is {}".format(sorted(B_columns)))
            print("N_columns is {}".format(sorted(N_columns)))
            print("\n")
            return is_optim, B_columns, N_columns

    def find_out_base(self, y, x_B):
        # 找到x_B/y最小且y>0的位置
        index = []
        min_value = []
        for i, value in enumerate(y):
            if value <= 0:
                continue
            else:
                index.append(i)
                min_value.append(x_B[i]/float(value))

        actual_index = index[np.argmin(min_value)]
        return actual_index


if __name__ == "__main__":
    '''
    c = np.array([-20, -30, 0, 0]).reshape(-1, 1)
    A = np.array([[1, 1, 1, 0], [0.1, 0.2, 0, 1]])
    b = np.array([100, 14]).reshape(-1, 1)
    '''
    c = np.array([-4, -1, 0, 0, 0]).reshape(-1, 1)
    A = np.array([[-1, 2, 1, 0, 0], [2, 3, 0, 1, 0], [1, -1, 0, 0, 1]])
    b = np.array([4, 12, 3]).reshape(-1, 1)
    simplex = Simplex(c, A, b)
    simplex.run()

实验结果：

Steps is 1
Not Reach Optimization
In Base is 0
Out Base is 4
B_columns is [0, 2, 3]
N_columns is [1, 4]

Steps is 2
Not Reach Optimization
In Base is 1
Out Base is 3
B_columns is [0, 1, 2]
N_columns is [3, 4]

Steps is 3
Reach Optimization.
B_columns is [2 1 0]
N_columns is [3, 4]
Best Solution Point is [5.8 1.2 4.2]
Best Value is -18.000000000000004

 

第五章 无约束最优化单纯形法的matlab实现 

5.1 无约束最优化单纯形法的matlab实现

 Matlab程序：

%% 单纯形
syms x1 x2 x3 x
f=x1.^2+x2.^2-x1*x2-10*x1-4*x2+60+(x3-2)^2;
X=DCX(f,[0 0 0],1.5,1.7,0.5,1e-10,100)
 
function minx=DCX(f,x0,h,gama,beta,eps,k)
% f  函数符号表达式
% x0 初始点
% h  初始单纯形构造因子
% gama 扩张因子
% beta 收缩因子
% eps
% k 
 
x0=x0';
X(:,1)=x0;%初始点x存储在顶点X的第一列
Num_var_f=length(symvar(f));%几维函数
%% 构造初始单纯形
for i = 1:Num_var_f %三维函数，需要四个顶点坐标
    x = zeros(Num_var_f,1);
    x(i) = x0(i) + h;
    X(:,i+1)=x;% 将单纯形按列存储
end
n=1;
tol = 1 ;
while n < k && tol > eps
    %% 计算函数值
    for i = 1:Num_var_f+1
        F_val(i)=double(subs(f,symvar(f),X(:,i)'));
    end
    [F_sort,F_index]=sort(F_val);%从小到大
    %最好点
    f_best=F_sort(1);
    X_best=X(:,F_index(1));
    %最差点
    f_bad=F_sort(end);
    X_bad=X(:,F_index(end));
    %次差点
    f_nextbad=F_sort(end-1);
    X_nextbad=X(:,F_index(end-1));
    % 计算形心
    tol=abs((f_bad-f_best)/f_best); 
    Xc=1/Num_var_f*sum(X(:,F_index(1:end-1)),2);
    
    %% 反射
    flag = 0;
    X_reflect=Xc+(Xc-X_bad);
    f_reflect=double(subs(f,symvar(f),X_reflect'));
    %比较反射之后 
    if f_best > f_reflect  % 反射点R<最好点，可以扩张
         X_reflect_expand=Xc+gama*(Xc-X_bad);%扩张
         f_reflect_expand=double(subs(f,symvar(f),X_reflect_expand'));
         if f_reflect_expand < f_reflect %扩张点继续缩小
             X(:,F_index(end)) = X_reflect_expand; %将其作为单纯性的新顶点
         else %否则
             X(:,F_index(end)) = X_reflect; %采用扩张前的点作为单纯形的新顶点
         end
         flag = 1; %反射成功标志位
    end
    if flag == 0  %说明没有反射成功
        if f_reflect < f_nextbad  %反射点<次差点
            X(:,F_index(end)) = X_reflect;%采用该反射点作为新的顶点
        else  % f_reflect >= f_nextbad
            if f_reflect < f_bad % 反射点要比最差点好一些
                X_reflect_shrink=Xc+beta*(X_reflect-Xc);% 收缩点
                f_reflect_shrink=double(subs(f,symvar(f),X_reflect_shrink'));
            else
                X_reflect_shrink=Xc+beta*(X_bad-Xc);% 收缩点
                f_reflect_shrink=double(subs(f,symvar(f),X_reflect_shrink'));
            end
            if f_reflect_shrink < f_bad
                X(:,F_index(end)) = X_reflect_shrink;
            else % 缩短边长
                X = X_best + 1/2 * (X-X_best);
            end
            
        end
    end
    n=n+1;
end
minx=X_best;
end

实验结果：

>> DCXingfa

X =

    8.0000
    6.0000
    2.0000

>> 

 

参考文献

[1]杨静蕾,张建勇,杨君泺.线性规划单纯形法的三种实现形式探析[J].大学数学,2020,36(04):68-73.

[2]李丰兵.探讨单纯形法的改进[J].科技资讯,2019,17(13):194-195.

[3]刘莹.运筹学中单纯形法的三种变量的教学研究[J].科教文汇(上旬刊),2017(05):36-37.

[4]孙秀华.单纯形法中的线性无关性[J].宜春学院学报,2015,37(12):26-27+86.

[5]高培旺.线性规划的原有松弛-对偶单纯形算法[J].高师理科刊,2015,35(07):10-13.

直接下载课程设计PDF