牛头刨床机构动力学的分析(C语言建模)

对于机械设计机构运动学与力学的分析，一般使用MATLAB软件进行计算和分析会比较方便。然鹅，在成功地下载MATLAB安装包失败后，咱们还是要玩点反常的东西，比如说，用C语言建模计算分析(ಡωಡ)。

Part 1.背景介绍

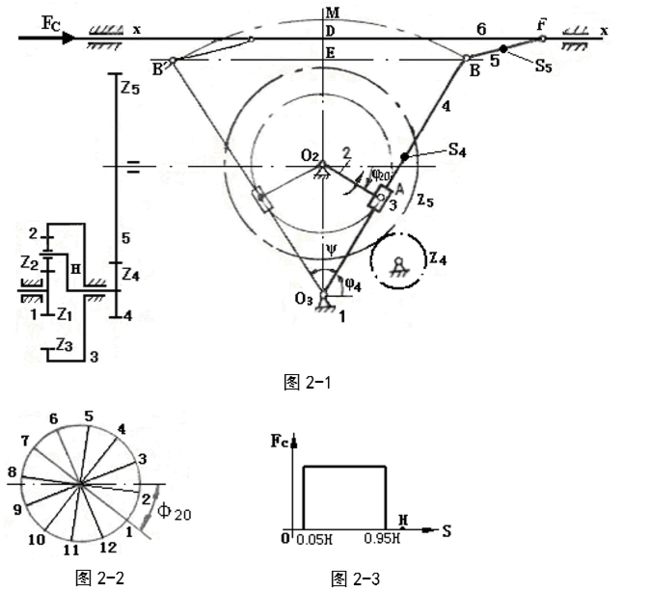
牛头刨床是一种用于平面加工的机床。如图2-1所示，电机通过行星轮系及齿轮Z4、Z5减速带动曲柄2转动。刨床工作时，由导杆机构（2、3、4、5、6）带动刨头及刨刀作往复运动。刨头向左时，刨刀进行切削，这个行程称为工作行程，此时要求刨头的速度低些，且作近似的等速运动。在工作行程，刨头受到较大的切削力，如图2-3所示。刨头右行时，刨刀不切削称为空回行程，此时希望刨头速度高些，以提高生产力。

太抽象了？咱们看一下动图吧(动图经过引用)：

Part 2.原始数据

如以下图表所示，参数符号含义分别为：H：刨头行程；K：行程速比系数； Fc：切削阻力；m4、m5、m6分别为导杆、连杆及刨头的质量；Js4、Js5分别为导杆4及连杆5绕各自质心的转动惯量；n1：电机转速；n2：曲柄2及齿轮5的转速； k：行星轮个数。

根据原始数据，我们可以计算出几个重要参数：

对程序变量进行设定并声明，我们取摆角的半角(41.5°/2=20.75°)，将原动件周期开始之前的半摆角设为原动件角度phi2的初始，即-20.75°。均匀取100个等分点作为原动件在每个等分角度点的角度(即每两个连续点之间相差3.6°)，后面的每个研究对象的位移、速度、加速度、受力分析均以原动件的每一个角度为参考标准，即他们的图像随着原动件角度的变化而变化。

#include
#include
#define Pi acos(-1.0)//Π的精确值 
#define N 100//均匀取N个点 
int main(){
	float H=0.55,L1=0.400,L2=0.1416,L3=0.776,L4=0.751,L5=0.233;
	float Z=Pi/180,w=80*Pi/30;
	float phi2[N],phi[N];
	float dphi=(float)360/N;//将360°圆周等分为N个微分 
	float dT=((float)1000/60)/N;//转速为1000rpm,取N个时间点 
	int i;
	for(i=0;i

Part 3.导杆机构的运动分析

由此，我们得到相对于参考系(即原动件角)时，杆L4、L5的的角位置和O3A(S3)、刨刀(L6)的绝对位移。

float S3[N],phi4[N],phi5[N],L6[N],S5[N];//L6为刨刀位移 
        FILE *fp;
	fp=fopen("角度与位移.xls","w");//生成测试文件(xls) 
fprintf(fp,"phi2\tS3\t\tphi2\tphi4\t\tphi2\tphi5\t\tphi2\tS6\n"); 
for(i=0;i

将生成的数据导入EXCEL表格，并插入图表，图像如下：

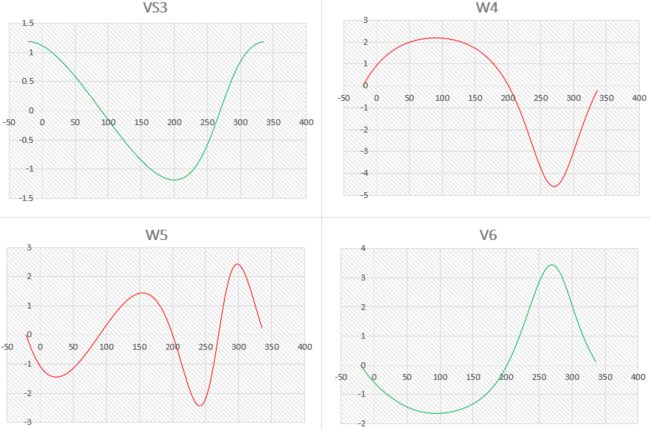
接着，我们求出它们的绝对速度，值得注意的是：S3‘、V5、V6是线速度，w4、w5是角速度：

float w4[N],w5[N],V5[N],V6[N];//构件4和构件5的角速度,杆5质心与刨刀6线速度 
float VS3[N];//构件3速度 
	FILE *fp1;
	fp1=fopen("速度.xls","w");
	fprintf(fp1,"phi2\tVS3\t\tphi2\tW4\t\tphi2\tW5\t\tphi2\tV6\n");  
	for(i=0;i

将生成的数据导入EXCEL表格，并插入图表，图像如下：

进一步地，求解加速度：

哎呀，面对这些乱七八糟的变量该咋办？别急，有图有真相：

将P-M·N矩阵用A、B、C、D字母表示，则：

        FILE *fp2;
	fp2=fopen("加速度.xls","w");
	fprintf(fp2,"phi2\taS3\t\tphi2\ta4\t\tphi2\ta5\t\tphi2\ta6\n"); 
	float aS3[N],a4[N],a5[N],a6[N];
	for(i=0;i

下一步操作->秀图：

Part 4.导杆机构的动态受力分析

在保留越程槽长度的范围内，允许有切削，否则不能切削 。基于此工作原理，可以写出计算切削阻力的程序：

float M4=15,M5=4,M6=58,Js4=0.7,Js5=0.025,Fc[N],Ls4,Ls5,E[N],dE[N],Mp[N],J4;
Ls4=0.5*L4;
Ls5=0.5*L5; 
FILE *fp3;
fp3=fopen("切削阻力.xls","w");
fprintf(fp3,"phi2\tFc\n"); 
for(i=0;i0.05*H&&fabs(L6[0]-L6[i])<0.95*H&&(phi2[i]

对于平衡力矩Mp，我们可以使用动能定理进行求解：

前面我们已求得V6、W5、W4，现在还剩一个V5没求，现在开始求吧：

由V5^2=V5x^2+V5y^2可得V5：

     for(i=0;i

but……何必那么麻烦？像V4=w4*L4/2那样直接套用公式V5=w5*L5/2来计算杆5的质心速度不就行了吗？

杆5被杆4连接，在这里，我们以点O3为参考点，w4既是杆4的相对角速度，又是绝对角速度，它当然可以直接用于求线速度。可之前求的w5是绝对角速度呀，它怎么能直接这样套公式呢，不信，咱们看看|V5/w5|的图像吧：

很明显，|V5/w5|的值不是常数，更不可能是L5/2。

接着，求完V5后可以直接套用公式求解平衡力矩了：

J4=Js4+M4*(0.5*L4)*(0.5*L4); 
FILE *fp4;
	fp4=fopen("平衡力矩.xls","w");
	fprintf(fp4,"phi2\tMp\n"); 
	for(i=0;i

以上是基于C语言实现牛头刨床机构动力学建模分析的全部内容，使用MATLAB效果相同，正经人表示->面对复杂的建模，还是建议使用MATLAB。如有错漏，欢迎指正~~~