python：关于三维装箱问题的算法研究-1

资源下载
先准备一个用来图显的函数

# -*- coding: utf-8 -*-
from matplotlib import pyplot as plt
#设置图表刻度等格式
from matplotlib.ticker import MultipleLocator, FormatStrFormatter 
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

#make_pic的内置函数，用来在图像里面不断添加立方体
def box(ax,x, y, z, dx, dy, dz, color='red'):
    xx = [x, x, x+dx, x+dx, x]
    yy = [y, y+dy, y+dy, y, y]
    kwargs = {
     'alpha': 1, 'color': color}
    ax.plot3D(xx, yy, [z]*5, **kwargs)#下底
    ax.plot3D(xx, yy, [z+dz]*5, **kwargs)#上底
    ax.plot3D([x, x], [y, y], [z, z+dz], **kwargs)
    ax.plot3D([x, x], [y+dy, y+dy], [z, z+dz], **kwargs)
    ax.plot3D([x+dx, x+dx], [y+dy, y+dy], [z, z+dz], **kwargs)
    ax.plot3D([x+dx, x+dx], [y, y], [z, z+dz], **kwargs)
    return ax
#显示图形的函数：Items = [[num[0],num[1],num[2],num[3],num[4],num[5],num[6]],]
#Items是N个列表的列表，里面的每个列表数据[放置点O三维坐标，长宽高，颜色]
def make_pic(Items):
    fig = plt.figure()
    ax = Axes3D(fig)
    ax.xaxis.set_major_locator(MultipleLocator(50)) 
    ax.yaxis.set_major_locator(MultipleLocator(50)) 
    ax.zaxis.set_major_locator(MultipleLocator(50)) 
    for num in Items:
        box(ax,num[0],num[1],num[2],num[3],num[4],num[5],num[6])
    plt.title('Cube')
    plt.show()
#根据图显需要的数据，把尺寸数据生成绘图数据的函数
def make(O,C,color):
    data = [O[0],O[1],O[2],C[0],C[1],C[2],color]
    return data

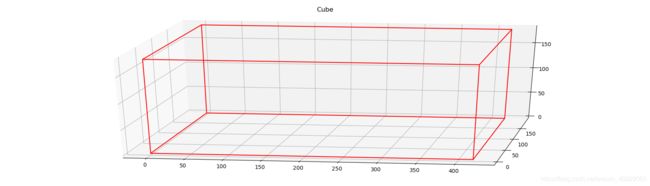
准备好图显函数后，先制作一个容器-货柜

#1.给定空间容器C      
#内容积为:长4.2x宽1.9x高1.8米
O = (0,0,0)           #原点坐标
C = (420,190,180)    #箱体长宽高
color = 'red'         #箱体颜色
#显示箱体
# make_pic([make(O,C,color)]) #这个为直接显示箱体看下效果
#show_num = [make(O,C,color)] #这个为后面组合显示时，把箱体显示数据添加到所有要显示的数据里面

接着制作N个需要装箱的货物

#2.给定有限量个方体 1200个(60,40,50)的方体
B=[]
for num in range(0,1200):
    B.append((60,40,50))
#如果在后面的考虑不同方体的装箱时，方体大小存在差异，我们将优先按照体积大小降序排列，优先摆放大体积的
#因为按照模拟装箱的情况，当大箱子摆放后产生的可放置点，能在上方放置边长不大于或者大于小部分的物体，可选物体范围更大

#3.拟人化依次堆叠方体，假设这里不考虑方体朝向/重心/堆叠限制，如果有大小差异考虑方体最大悬空面积为30%
#第一个方体的位置从原点开始
color2='blue'
show_num.append(make(O,B[0],color2))
make_pic(show_num)#查看图显效果

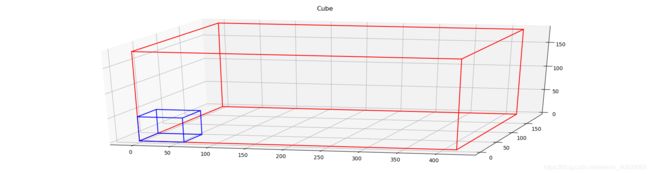
由图片我们可以看到，每放置一个货物，就会消耗一个放置点，并且产生三个新的放置点

当然，这里最少有两个情况需要注意：
1.当因为货物大小和残余空间不足的时候，放置点也会失效
2.如果货物的长宽高有一项一致时，可能会产生相同的放置点（发生放置点覆盖），我们在计算放置点的时候，要保证放置点是唯一的

这里按照放置点产生的逻辑，写一个放置点产生函数

#可用点的生成方法
def newsite(O,B_i):
    # 在X轴方向上生成
    O1 = (O[0]+B_i[0],O[1],O[2])
    # 在Y轴方向上生成
    O2 = (O[0],O[1]+B_i[1],O[2])
    # 在Z轴方向上生成
    O3 = (O[0],O[1],O[2]+B_i[2])
    return [O1,O2,O3]
#这个时候新产生3个可用摆放点，把放入第一个货物时产生的三个放置点加入放置点列表
O_items = []
O_items = O_items + newsite(O,B[0])

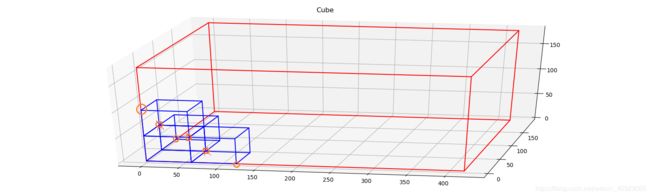
所以根据这三个放置点，我们又可以进行货物堆叠，并产生新的放置点

#所以在新的点位上摆放新的箱子,同时生成逻辑上的新的三个点
#实际好像当箱体一样大的时候没有三个点，而且当箱体体积接近时，有的点无法使用
#后期解决方法为当点可用性不够时，优先在水平面扩散，让点可用
show_num.append(make(O_items[0],B[1],color2))
O_items = O_items + newsite(O_items[0],B[1])

show_num.append(make(O_items[1],B[2],color2))
O_items = O_items + newsite(O_items[1],B[2])

show_num.append(make(O_items[2],B[3],color2))
O_items = O_items + newsite(O_items[2],B[3])

按照图显可以看到，实际在"打X"的三个点的放置点发生了覆盖

开始写我们的放置逻辑

所以从第二个货物开始，我们就开始重复性的发生货物的堆叠
并重复性的产生新的放置点，直到放置点不再可用

#所以从我们的仓库B不断的把货物B_i搬到箱体里，限制条件为在X,Y,Z方向上可用点小于箱体长宽高
canput = 1 #初始放了一个货物

for i in range(1,len(B)):
    #货物次序应小于等于可用点数量，如：第四个货物i=4，使用列表内的第三个放置点O_items[2]，所以i-1应小于等于len-1
    if i-1 <= len(O_items)-1:
        #如果放置点放置货物后，三个方向都不会超过箱体限制
        if O_items[i-1][0]+B[i][0]<=C[0] and O_items[i-1][1]+B[i][1]<=C[1] and O_items[i-1][2]+B[i][2]<=C[2]:
            #使用放置点，添加一个图显信息
            show_num.append(make(O_items[i-1],B[i],color2))
            #计数加1
            canput = canput + 1
            #把堆叠后产生的新的点，加入放置点列表
            for new_O in newsite(O_items[i-1],B[i]):
                #保证放入的可用点是不重复的
                if new_O not in O_items:
                    O_items.append(new_O)
        
        #如果轮到的这个放置点不可用
        else:
            #把这个可用点弹出弃用
            O_items.pop(i-1)
            #弃用可用点后，货物次序应小于等于剩余可用点数量
            if i-1 <= len(O_items)-1:
                #当可用点一直不可用时
                while O_items[i-1][0]+B[i][0]>C[0] or O_items[i-1][1]+B[i][1]>C[1] or O_items[i-1][2]+B[i][2]>C[2]:
                    #一直把可用点弹出弃用
                    O_items.pop(i-1)
                    #如果弹出后货物次序超出剩余可用点，则认为无法继续放置
                    if i-1 > len(O_items)-1:
                        break
                #货物次序应小于等于剩余可用点数量
                if i-1 <= len(O_items)-1:
                    #如果不再超出限制，在这个可用点上堆叠
                    show_num.append(make(O_items[i-1],B[i],color2))
                    #计数加1
                    canput = canput + 1
                    #把堆叠后产生的新的点，加入放置点列表
                    for new_O in newsite(O_items[i-1],B[i]):
                        #保证放入的可用点是不重复的
                        if new_O not in O_items:
                            O_items.append(new_O)

print(canput)
make_pic(show_num)

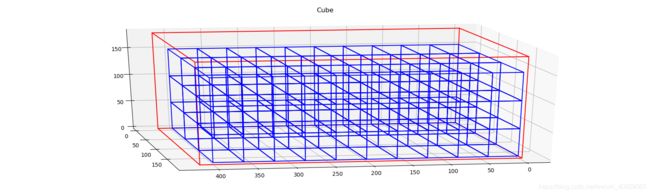
最终运行结果：canput = 84

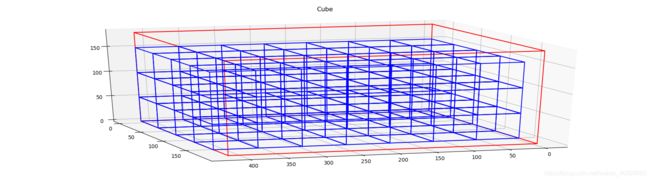
可以看到装箱后在上部和侧部仍有较大剩余空间

结论：如果在货物摆放方向和朝向固定的时候，最大装货量为84/箱

但是我们在实际装箱的时候，如果没有特殊限定，
货物的三个边a，b，c选为底边的组合方式应该有：（a,b),（b,a),（a,c),（c,a),（b,c),（c,b)六种方式

在简单由原来的60-40-50修改为40-60-50之后，装箱的空间利用率马上上升为了90/箱

很明显，每个货物摆放之后，因为摆放朝向的六种可能，剩余点的可用性也会发生改变
也就是说，假设装载数为80-90/箱时，理想摆放方案数为6的80-90次方左右

既然要考虑货物朝向的可利用性，那就要考虑货物大小，最大悬空比例，因为朝向不一致带来的放置点不可用问题，这里接下来的思路是，货物和货物之间的位差也会产生新的放置点且放置点的可用受限于被贴合货物的大小。