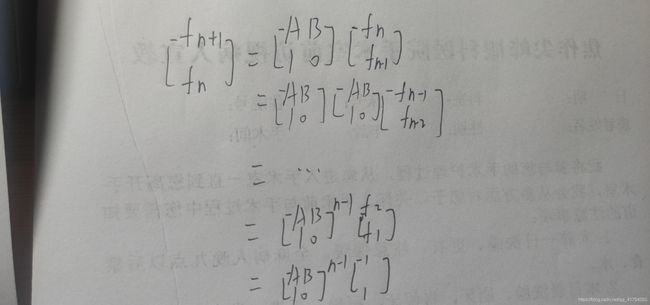矩阵乘法快速幂
今天员工小c写题的时候遇到了在第四黑厂时期就没填的坑,今日再次见面,自然是无奈,但是他请教了他的好朋友枫系,原来需要矩阵乘法快速幂的知识。
Number Sequence
时间限制: 1 Sec 内存限制: 256 MB
题目描述
此题HDUOJ数据过水,网上题解中直接将n%49的做法是错误的。
A number sequence is defined as follows:
f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.
Given A, B, and n, you are to calculate the value of f(n).
输入
The input consists of multiple test cases. Each test case contains 3 integers A, B and n on a single line (1 <= A, B <= 1000, 1 <= n <= 100,000,000). Three zeros signal the end of input and this test case is not to be processed.
输出
For each test case, print the value of f(n) on a single line.
样例输入
1 1 3
1 2 10
0 0 0
样例输出
2
5这就是小c遇到的题目,小c最早找规律半天也没找出来,就去问度娘,结果度娘所有答案都是%49,小C一看,稳了,马上又A一题。(第n次不读题,题上说了%49错的) Ctrl C+Ctrl V = WA。非常尴尬。
然后小c没办法呀,只能请教他的新朋友枫系,枫系二话不说,就很仗义地把自己的代码展示给了小C,小C一看两看三看四看都看不明白,后来才知道这是矩阵乘法快速幂,可惜网上的博客并没有教会小C,于是小C只能再次求助枫系。
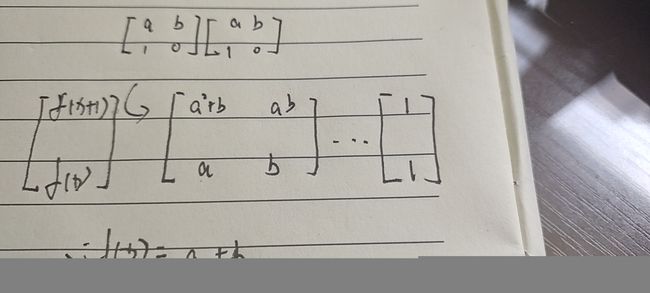
原来矩阵乘法快速幂需要线性代数的知识,还好小C也是个带学生。这题看似是斐波那契递推的升级版,实则应该采用矩阵的方法优化。
图片来自枫系。说实话这个图清晰明了,网上博客要是有个这图,小C早会了(逃
这是代码,也可以当作模板采用,注释的非常详细。
#include//本代码来自于一位小c的好朋友枫系,向他表示感谢,他教会了我,我才能教给大家
using namespace std;
struct juzhen
{
int x[2][2];//定义一个矩阵
};
juzhen mul(juzhen a,juzhen b)//这个部分是用作矩阵相乘的模拟;
{
juzhen c;//定义一个矩阵类型的c
memset(c.x,0,sizeof(c.x));//将c初始化
for(int i=0;i<2;i++)//矩阵乘法大模拟
for(int j=0;j<2;j++)//这个需要学过线性代数才能模拟
for(int k=0;k<2;k++)//线性代数应该是大一的东西
c.x[i][j]=(c.x[i][j]+a.x[i][k]*b.x[k][j])%7;//当然也不是很难,百度看一看就会了
return c;
}
juzhen pow(juzhen now,int n)//矩阵版本的快速幂
{
juzhen ans;//定义一个juzhen类型的ans,矩阵初始化*4,main函数那里说了
ans.x[0][0]=1;//左上角a 矩阵
ans.x[0][1]=0;//右上角b a b
ans.x[1][0]=0;//左下角1 1 0
ans.x[1][1]=1;//右下角0
while(n)
{
if(n&1)//如果这一位是1
ans=mul(ans,now);//ans就乘以一下
now=mul(now,now);//now进位
n=n/2;//n右移一位
}
return ans;//返回ans
}
void print(juzhen a)//此处是用来在写矩阵的时候检查用的,交代码的时候不调用,不是我的代码,就把它留作纪念吧
{
for(int i=0;i<2;i++)
{
for(int j=0;j<2;j++)
cout<>a>>b>>c;!(a==0&&b==0&&c==0);cin>>a>>b>>c)
{
if(c==1||c==2)//一和二就直接输出吧
cout<<1;
else
{
juzhen ans;//定义一个juzhen类型的ans
ans.x[0][0]=a;//左上角a 矩阵
ans.x[0][1]=b;//右上角b a b
ans.x[1][0]=1;//左下角1 1 0
ans.x[1][1]=0;//右下角0
ans=pow(ans,c-1);//跟快速幂一样
cout<<(ans.x[1][0]+ans.x[1][1])%7;//输出题目要求的%7 f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.
}
cout<
?
#include//本代码来自于一位小c的好朋友枫系,向他表示感谢,他教会了我,我才能教给大家
using namespace std;
struct juzhen
{
int x[2][2];//定义一个矩阵
};
juzhen mul(juzhen a,juzhen b)//这个部分是用作矩阵相乘的模拟;
{
juzhen c;//定义一个矩阵类型的c
memset(c.x,0,sizeof(c.x));//将c初始化
for(int i=0;i<2;i++)//矩阵乘法大模拟
for(int j=0;j<2;j++)//这个需要学过线性代数才能模拟
for(int k=0;k<2;k++)//线性代数应该是大一的东西
c.x[i][j]=(c.x[i][j]+a.x[i][k]*b.x[k][j])%7;//当然也不是很难,百度看一看就会了
return c;
}
juzhen pow(juzhen now,int n)//矩阵版本的快速幂
{
juzhen ans;//定义一个juzhen类型的ans,矩阵初始化*4,main函数那里说了
ans.x[0][0]=1;//左上角a 矩阵
ans.x[0][1]=0;//右上角b a b
ans.x[1][0]=0;//左下角1 1 0
ans.x[1][1]=1;//右下角0
while(n)
{
if(n&1)//如果这一位是1
ans=mul(ans,now);//ans就乘以一下
now=mul(now,now);//now进位
n=n/2;//n右移一位
}
return ans;//返回ans
}
void print(juzhen a)//此处是用来在写矩阵的时候检查用的,交代码的时候不调用,不是我的代码,就把它留作纪念吧
{
for(int i=0;i<2;i++)
{
for(int j=0;j<2;j++)
cout<>a>>b>>c;!(a==0&&b==0&&c==0);cin>>a>>b>>c)
{
if(c==1||c==2)//一和二就直接输出吧
cout<<1;
else
{
juzhen ans;//定义一个juzhen类型的ans
ans.x[0][0]=a;//左上角a 矩阵
ans.x[0][1]=b;//右上角b a b
ans.x[1][0]=1;//左下角1 1 0
ans.x[1][1]=0;//右下角0
ans=pow(ans,c-1);//跟快速幂一样
cout<<(ans.x[1][0]+ans.x[1][1])%7;//解释看下方图片
}
cout<