LeetCode:1631.最小体力消耗路径——中等
题目:
1631.最小体力消耗路径
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights [ row ][ col ] 表示格子 ( row, col ) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
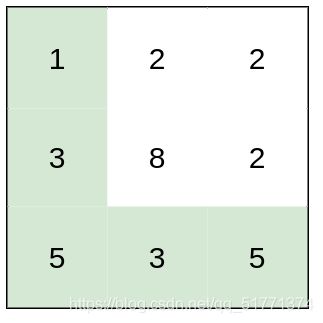
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
示例 2:
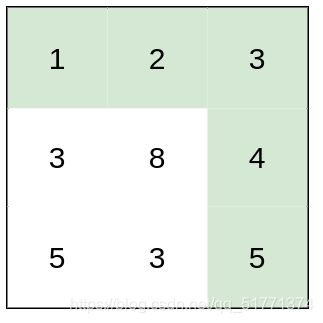
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
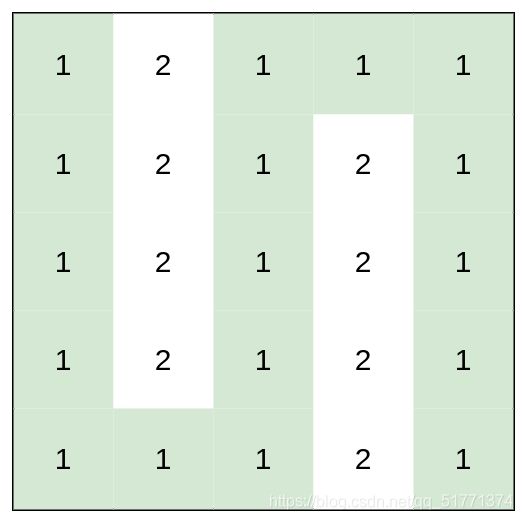
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
- rows == heights.length
- columns == heights[i].length
- 1 <= rows, columns <= 100
- 1 <= heights[i][j] <= 106
解题思路:
根据二维数组,以每一个点为基础初始化并查集p,然后建立边的集合edges,记录相邻位置的两点(下,左)及其绝对值差,对在edges的边,合并并查集,记录最大cost。当p[0]与p[-1]连通是,返回cost
代码:
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
# 当数组仅有第一个元素时
if len(heights) < 2 and len(heights[0]) < 2:
return 0
# 当数组只有一行时
if len(heights) == 1:
cost = 0
for j in range(1, len(heights[0])):
cost = max(cost, abs(heights[0][j] - heights[0][j-1]))
return cost
# 当数组只有一列时
if len(heights[0]) == 1:
cost = 0
for i in range(1, len(heights)):
cost = max(cost, abs(heights[i][0] - heights[i-1][0]))
return cost
# 初始化并查集
num = len(heights) * len(heights[0])
p = [[i] for i in range(num)]
edges = []
# 对每个元素,对左边、下班元素,建立边的集合,形式为[x, y, gap]
for i in range(len(heights)):
for j in range(len(heights[0])):
pointX = i * len(heights[0]) + j
if j <= len(heights[0]) - 2:
pointY = i * len(heights[0]) + j + 1
gap = abs(heights[i][j] - heights[i][j+1])
edges.append([pointX, pointY, gap])
if i <= len(heights) - 2:
pointY = (i+1) * len(heights[0]) + j
gap = abs(heights[i][j] - heights[i+1][j])
edges.append([pointX, pointY, gap])
# 并查集的合并操作
cost = 0
edges.sort(key = lambda x:x[-1])
for edge in edges:
if p[0] is p[-1]:
return cost
else:
x, y, gap = edge
if p[x] is not p[y]:
cost = max(gap, cost)
p[x].extend(p[y])
for z in p[x]:
p[z] = p[x]
提交记录:
然后昨天刚学了一下Kruskal算法,不过还不是很懂,就跟着别人的题解敲了一遍(手动黑脸)
class UnionFindSet:
def __init__(self, elements):
self.father = {
}
self.rank = {
}
for element in elements:
self.father[element] = element
self.rank[element] = 1
def find_head(self, element):
stack = []
while element != self.father[element]:
stack.append(element)
element = self.father[element]
while stack:
self.father[stack.pop()] = element
return element
def union(self, element1, element2):
head1 = self.find_head(element1)
head2 = self.find_head(element2)
if head1 == head2:
return
if self.rank[head1] < self.rank[head2]:
head1, head2 = head2, head1
self.rank[head1] += self.rank[head2]
self.rank.pop(head2)
self.father[head2] = head1
def is_name_set(self, element1, element2):
head1 = self.find_head(element1)
head2 = self.find_head(element2)
if head1 == head2:
return True
else:
return False
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
if not len(heights) or not len(heights[0]):
return 0
elements = [(i, j) for i in range(len(heights)) for j in range(len(heights[0]))]
edges = []
for i in range(len(heights)):
for j in range(len(heights[0])):
if i > 0:
edge = [abs(heights[i][j] - heights[i-1][j]), (i, j), (i-1, j)]
edges.append(edge)
if i < len(heights) - 1:
edge = [abs(heights[i][j] - heights[i+1][j]), (i, j), (i+1, j)]
edges.append(edge)
if j > 0:
edge = [abs(heights[i][j] - heights[i][j-1]), (i, j), (i, j-1)]
edges.append(edge)
if j < len(heights[0]) - 1:
edge = [abs(heights[i][j] - heights[i][j+1]), (i, j), (i, j+1)]
edges.append(edge)
ufs = UnionFindSet(elements)
edges.sort()
start = (0, 0)
end = (len(heights)-1, len(heights[0])-1)
ret = 0
for weight, v1, v2 in edges:
if ufs.is_name_set(start, end):
return ret
if ufs.is_name_set(v1, v2):
pass
else:
ufs.union(v1, v2)
ret = weight
return ret