数值分析第三次大作业
数值分析第三次大作业
算法设计方案
- 对二维数组,做f关于t,u的分片二次插值,根据插值节点,形成16个二元二次函数。
- 对每一组 xi=0.08∗i,yj=0.5+0.05∗j(i=0,1,⋯,10,j=0,1,⋯,20) 带入方程组,用迭代法求解出相对应的t,u,根据t,u的取值范围,选择合适的二元二次插值函数,求出 f(xi,yj) .
对于 k=0,1,⋯,10 ,使用最小二乘法法求出f(x,y)在区域 D={ (x,y)|0≤x≤0.8,0.5≤y≤1.5} 的近似表达式
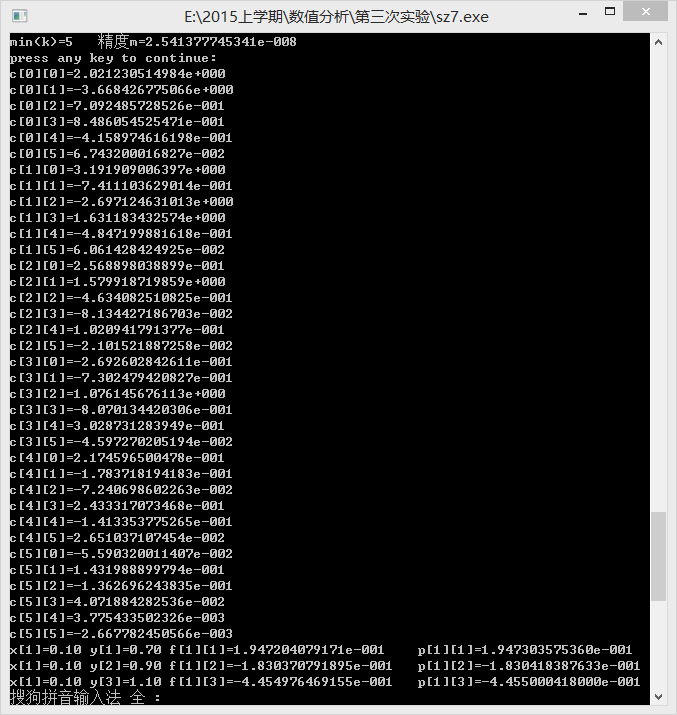
p(x,y)=∑r=0k∑s=0kcrsxrys ,其中 { xr}r=kr=0,{ ys}s=ks=0 是基函数,具体算法如下:- 固定 yj ,以 { xr}r=kr=0 为基函数对 (xi,fij) 作最小二乘拟合,得到的系数矩阵记为B,同理固定x,以 { ys}s=ks=0 基函数获得系数矩阵G
- 对矩阵 (BTB)A=BTF , (GTG)CT=(AG)T ,分别以 BTB,GTG 为系数矩阵,以 BTF的每一列,AG 的每一行分别作为线性方程组的右半部分,利用顺序高斯消去法,求解出拟合函数的系数矩阵 C
- 求解出该k值下,拟合函数的精度
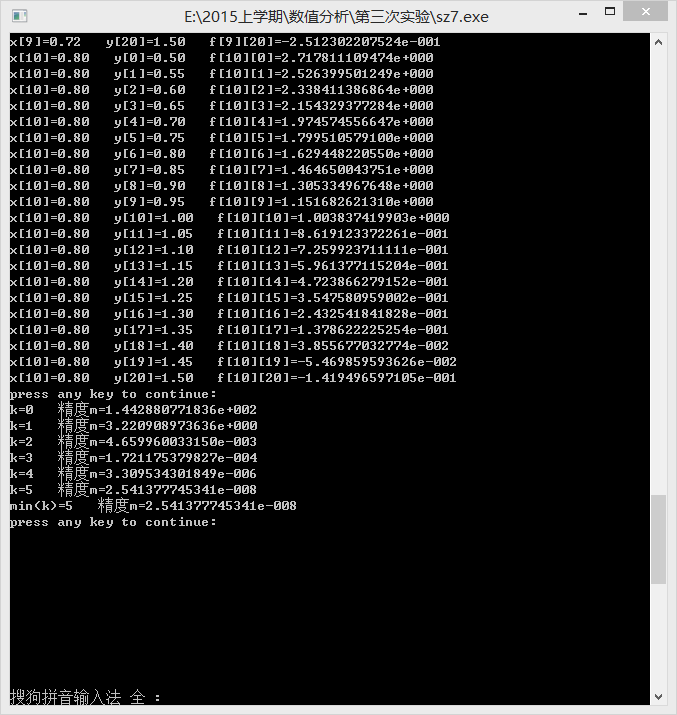
σ=∑i=010∑j=020[f(xi,yj)−p(xi,yj)]2
若 σ≤10−7 ,则找到最小k值,停止循环,此时系数矩阵C即为所求。
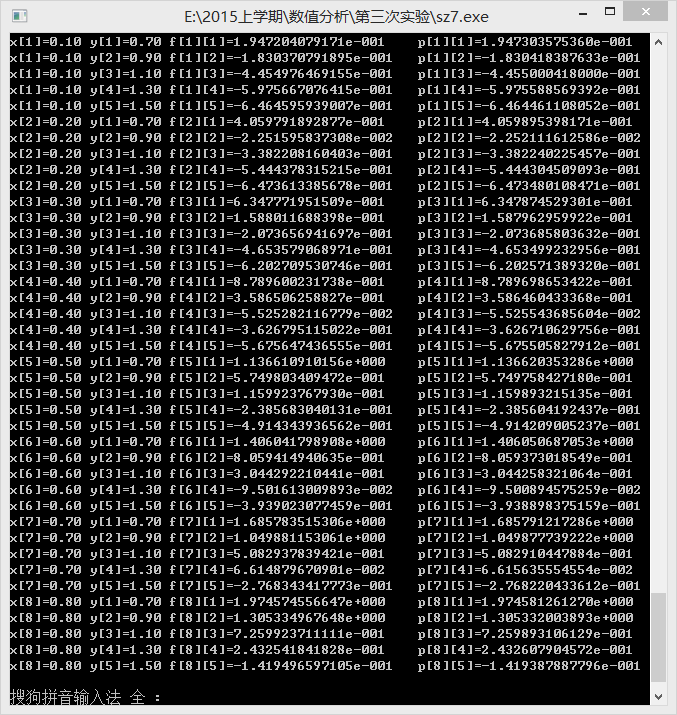
初始化p(x,y),对 xi=0.1∗i,yj=0.5+0.2∗j(i=1,2,⋯,8;j=1,2,⋯,5) ,重新计算
f(xi,yj) 以及 p(x∗i,y∗j) .
讨论分析
- 初始,我打算通过每一组确定(t,u)带入方程组求出(x,y),然而,如此一来,所求(x,y)未必均匀分布,因而无法使用分片二次插值,后来通过每一组 (xi,yj) ,带入非线性方程组,求解出(t,u),根据(t,u)与z的分片二次插值间接求解出 f(xi,yj) 。
- 计算拟合函数的系数矩阵C的时候,开始时直接套公式
C=(BTB)−1BTUG(GTG)−1
然而如此计算的结果 C 的数值非常大,在寻找原因的时候发现,求逆过程中,主元素的值远小于1,因此形成病态方程组,求逆结果数值非常大,而且,舍入误差的存在也使得尽管理论正确的算法,结果出现错误。后来间接求解 (BTB)A=BTF , (GTG)CT=(AG)T ,获得合适的结果。
源程序
#includereturn x;
}
void Nonlinear(double x,double y)
{
double g[5]={
0};
double v,w,t1,u1,v1,w1,norm;
double minu,maxu,maxt,mint;
int k;
v=0.5;
w=0.5;
t=0.5;
u=0.5;
for(k=1;k<10000;k++)
{
t1=t;
u1=u;
v1=v;
w1=w;
g[1]=0.5*cos(t)+u+v+w-x-2.67;
g[2]=t+0.5*sin(u)+v+w-y-1.07;
g[3]=0.5*t+u+cos(v)+w-x-3.74;
g[4]=t+0.5*u+v+sin(w)-y-0.79;
t=(-0.8*g[1]+1*g[2]+0*g[3]+1*g[4]+-2*t)/-2;
u=(1*g[1]+-1*g[2]+1*g[3]+-1*g[4]+-1*u)/-1;
v=(-1*g[1]+0*g[2]+1*g[3]+0*g[4]+1*v)/(1);
w=(-0*g[1]+-1*g[2]+0*g[3]+1*g[4]+1*w)/(1);
norm=max(max(max(fabs(t-t1),fabs(u-u1)),fabs(v-v1)),fabs(w-w1));
if(norm/max(max(max(fabs(t),fabs(u)),fabs(v)),fabs(w))<=1e-12)
{
break;
}
}
}
double Interpolation(double x,double y)
{
double l1,l2,p=0,tt[6],uu[6];
double z[6][6]={
{-0.5,-0.34,0.14,0.94,2.06,3.5},
{-0.42,-0.5,-0.26,0.3,1.18,2.38},
{-0.18,-0.5,-0.5,-0.18,0.46,1.42},
{
0.22,-0.34,-0.58,-0.5,-0.1,0.62},
{
0.78,-0.02,-0.5,-0.66,-0.5,-0.02},
{
1.5,0.46,-0.26,-0.66,-0.74,-0.5}};
int i,j,k,r,s;
for(i=0;i<6;i++)
{
tt[i]=0.2*i;
uu[i]=0.4*i;
}
if(x<=0.3)i=1;
if(x>0.3&&x<=0.5)i=2;
if(x>0.5&&x<=0.7)i=3;
if(x>0.7)i=4;
if(y<=0.6)j=1;
if(y>0.6&&y<=1.0)j=2;
if(y>1.0&&y<=1.4)j=3;
if(y>1.4)j=4;
for(k=i-1;k<=i+1;k++)
{
l1=1;
for(s=i-1;sfor(s=k+1;s<=i+1;s++)
l1=l1*(x-tt[s])/(tt[k]-tt[s]);
for(r=j-1;r<=j+1;r++)
{
l2=1;
for(s=j-1;sfor(s=r+1;s<=j+1;s++)
l2=l2*(y-uu[s])/(uu[r]-uu[s]);
p=p+l1*l2*z[k][r];
}
}
return p;
}
int main()
{
int i,j,k,s,r;
double v[21][21],v1[21][21],b[21][21],g[21][21],g1[21][21];
double f[11][21],p[21][21],a[21][21],c1[21][21]=,c[21][21];
double vv[10][10],gg[10][10],x[11],y[21],m,sum;
for(i=0;i<=10;i++)
{
x[i]=0.08*i;
for(j=0;j<=20;j++)
{
y[j]=0.5+0.05*j;
Nonlinear(x[i],y[j]);
f[i][j]=Interpolation(t,u);
printf("x[%d]=%-7.2fy[%d]=%-7.2ff[%d][%d]=%-30.12e\n",i,x[i],j,y[j],i,j,f[i][j]);
}
}
printf("press any key to continue:\n");
getch();
for(k=0;k<=10;k++)
{
for(i=0;i<=20;i++)
for(j=0;j<=20;j++)
{
v[i][j]=0;
v1[i][j]=0;
g1[i][j]=0;
a[i][j]=0;
c1[i][j]=0;
p[i][j]=0;
}
for(i=0;i<=10;i++)//B
for(j=0;j<=k;j++)
b[i][j]=pow(x[i],j);
for(i=0;i<=k;i++)//v=B^T*B
for(j=0;j<=k;j++)
for(r=0;r<=10;r++)
v[i][j]=v[i][j]+b[r][i]*b[r][j];
for(i=0;i<=k;i++)//v1=B^T*f
for(j=0;j<=20;j++)
for(r=0;r<=10;r++)
v1[i][j]=v1[i][j]+b[r][i]*f[r][j];
for(s=0;s<=20;s++)//V*A=V1
{
for(i=0;i<=k;i++)
{
for(j=0;j<=k;j++)
vv[i][j]=v[i][j];
}
for(r=0;r//消元过程
{
for(i=r+1;i<=k;i++)
{
m=vv[i][r]/vv[r][r];
for(j=r+1;j<=k;j++)
vv[i][j]=vv[i][j]-m*vv[r][j];
v1[i][s]=v1[i][s]-m*v1[r][s];
}
}
for(r=k;r>=0;r--)//回代过程
{
for(j=r+1,sum=0;j<=k;j++)
sum=sum+vv[r][j]*a[j][s];
a[r][s]=(v1[r][s]-sum)/vv[r][r];
}
}
for(i=0;i<=20;i++)//G
for(j=0;j<=k;j++)
g[i][j]=pow(y[i],j);
for(i=0;i<=k;i++)//G1=G^T*G
{
for(j=0;j<=k;j++)
{
for(r=0;r<=20;r++)
g1[i][j]=g1[i][j]+g[r][i]*g[r][j];
}
}
for(i=0;i<=k;i++)//C1=A*G
{
for(j=0;j<=k;j++)
for(r=0;r<=20;r++)
c1[i][j]=c1[i][j]+a[i][r]*g[r][j];
}
for(s=0;s<=k;s++)//G1*C^T=C1^T
{
for(i=0;i<=k;i++)
{
for(j=0;j<=k;j++)
gg[i][j]=g1[i][j];
}
for(r=0;r//消元过程
{
for(i=r+1;i<=k;i++)
{
m=gg[i][r]/gg[r][r];
for(j=r+1;j<=k;j++)
gg[i][j]=gg[i][j]-m*gg[r][j];
c1[s][i]=c1[s][i]-m*c1[s][r];
}
}
for(r=k;r>=0;r--)//回代过程
{
for(j=r+1,sum=0;j<=k;j++)
{sum=sum+gg[r][j]*c[s][j];}
c[s][r]=(c1[s][r]-sum)/gg[r][r];
}
}
m=0;
for(i=0;i<=10;i++)
{
for(j=0;j<=20;j++)
{
for(r=0;r<=k;r++)
{
for(s=0;s<=k;s++)
p[i][j]=p[i][j]+c[r][s]*pow(x[i],r)*pow(y[j],s);
}
m=m+pow(f[i][j]-p[i][j],2);
}
}
printf("k=%d 精度m=%.12e\n",k,m);
if(m<=1e-7)
{
printf("min(k)=%d 精度m=%.12e\n",k,m);
printf("press any key to continue:\n");
getch();
for(i=0;i<=k;i++)
{
for(j=0;j<=k;j++)
printf("c[%d][%d]=%.12e\n",i,j,c[i][j]);
}
break;
}
}
for(i=0;i<10;i++)
for(j=0;j<10;j++)
p[i][j]=0;
for(i=1;i<=8;i++)
{
x[i]=0.1*i;
for(j=1;j<=5;j++)
{
y[j]=0.5+0.2*j;
Nonlinear(x[i],y[j]);
f[i][j]=Interpolation(t,u);
for(r=0;r<=k;r++)
{
for(s=0;s<=k;s++)
p[i][j]=p[i][j]+c[r][s]*pow(x[i],r)*pow(y[j],s);
}
printf("x[%d]=%-5.2fy[%d]=%-5.2ff[%d][%d]=%-23.12ep[%d][%d]=%-20.12e\n",i,x[i],j,y[j],i,j,f[i][j],i,j,p[i][j]);
}
}
return 0;
}
程序结果
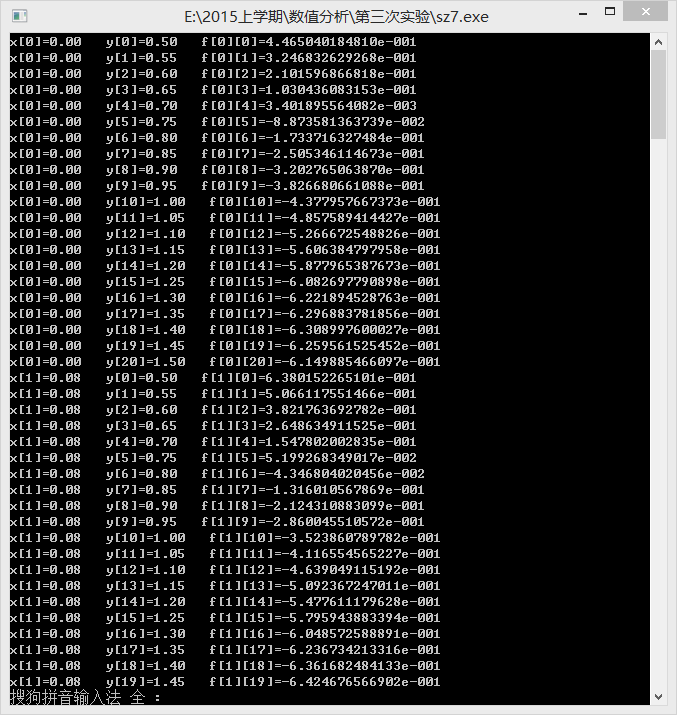
数组 (xi,yj,f(xi,yj))
选择过程中的 k,σ
达到精度要求时的 k,σ, 以及 p(x,y) 中的系数 crs
数表: