PyTorch - 21 - CNN Forward方法 - PyTorch深度学习实现

Neural Network Programming Series (Recap)

到目前为止，在本系列文章中，我们已经准备好了数据，现在正在构建模型。

我们通过扩展nn.Module PyTorch基类来创建网络，然后在类构造函数中将网络层定义为类属性。 现在，我们需要实现网络的forward（）方法，然后，最后，我们将准备训练我们的模型。

1. 准备数据
2. 建立模型
   a. 创建一个扩展nn.Module基类的神经网络类。
   b. 在类构造函数中，将网络的图层定义为类属性。
   c. 使用网络的图层属性以及nn.functional API操作来定义网络的前向传递。
3. 训练模型
4. 分析模型的结果

Reviewing The Network

目前，我们知道forward（）方法接受张量作为输入，然后返回张量作为输出。现在，返回的张量与传递的张量相同。

但是，在构建实现​​之后，返回的张量将是网络的输出。

这意味着正向方法实现将使用我们在构造函数内部定义的所有层。这样，前向方法显式定义了网络的转换。

forward（）方法是实际的网络转换。正向方法是将输入张量映射到预测输出张量的映射。让我们看看这是如何完成的。

回想一下，在网络的构造函数中，我们可以看到定义了五层。

class Network(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)

        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
        self.fc2 = nn.Linear(in_features=120, out_features=60)
        self.out = nn.Linear(in_features=60, out_features=10)

    def forward(self, t):
        # implement the forward pass      
        return t

我们有两个卷积层和三个线性层。如果我们对输入层进行计数，这将为我们提供一个总共六层的网络。

Implementing The forward()Method

让我们对此进行编码。 我们将从输入层开始。

Input Layer #1

任何神经网络的输入层都由输入数据确定。 例如，如果我们的输入张量包含三个元素，那么我们的网络将在其输入层中包含三个节点。

因此，我们可以将输入层视为身份转换。 从数学上讲，这是函数
$$f(x)=x$$
我们给任何 x 作为输入，然后得到与输出相同 x 的值。 无论我们使用的是具有三个元素的张量，还是表示具有三个通道的图像的张量，此逻辑都是相同的。 输入是数据输出！

这非常琐碎，这就是使用神经网络API时通常看不到输入层的原因。 输入层隐式存在。

绝对不是必需的，但是为了完整起见，我们将在forward方法中显示标识操作。

# (1) input layer
t = t

Hidden Convolutional Layers: Layers #2 And #3

就执行转换而言，两个隐藏的卷积层都将非常相似。 在深度学习基础知识系列中，我们在文章的层上解释了所有不是输入层或输出层的层都称为隐藏层，这就是为什么我们将这些卷积层称为隐藏层。

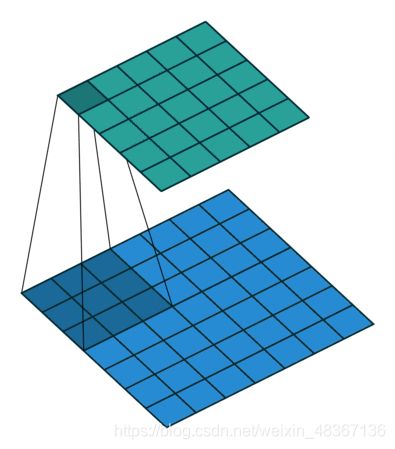
为了执行卷积运算，我们将张量传递给第一个卷积层的正向方法self.conv1。我们已经了解了所有PyTorch神经网络模块如何具有forward（）方法，并且当我们调用nn.Module的forward（）方法时，有一种特殊的调用方法。

当要调用nn.Module实例的forward（）方法时，我们将调用实际实例，而不是直接调用forward（）方法。

代替执行此self.conv1.forward（tensor），我们执行此self.conv1（tensor）。确保您看到了本系列的上一篇文章，以了解有关此内容的所有详细信息。

让我们继续并添加实现两个卷积层所需的所有调用。

# (2) hidden conv layer
t = self.conv1(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)

# (3) hidden conv layer
t = self.conv2(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)

正如我们在这里看到的那样，当我们在卷积层中移动时，输入张量将发生变换。第一卷积层具有卷积运算，然后是relu激活运算，其输出随后传递到kernel_size = 2和stride = 2的最大池运算中。

然后将第一个卷积层的输出张量t传递到下一个卷积层，除了我们调用self.conv2（）而不是self.conv1（）之外，其他卷积层均相同。

这些层中的每一个都由权重（数据）和收集操作（代码）组成。权重封装在nn.Conv2d（）类实例中。 relu（）和max_pool2d（）调用只是纯操作。这些都不具有权重，这就是为什么我们直接从nn.functional API调用它们的原因。

有时，我们可能会看到称为池化层的池化操作。有时我们甚至可能听到称为激活层的激活操作。

但是，使层不同于操作的是层具有权重。由于池操作和激活功能没有权重，因此我们将它们称为操作，并将其视为已添加到图层操作集合中。

例如，我们说网络中的第二层是一个卷积层，它包含权重的集合，并执行三个操作，即卷积操作，relu激活操作和最大池操作。

请注意，此处的规则和术语并不严格。这只是描述网络的一种方式。还有其他表达这些想法的方法。我们需要知道的主要事情是哪些操作是使用权重定义的，哪些操作不使用任何权重。

从历史上看，使用权重定义的操作就是我们所说的图层。后来，其他操作被添加到混合中，例如激活功能和池化操作，这引起了术语上的一些混乱。

从数学上来说，整个网络只是功能的组合，功能的组合就是功能本身。因此，网络只是一种功能。诸如图层，激活功能和权重之类的所有术语仅用于帮助描述不同的部分。

不要让这些术语混淆整个网络只是功能的组合这一事实，而我们现在正在做的就是在forward（）方法中定义这种组合。

Hidden Linear Layers: Layers #4 And #5

在将输入传递到第一个隐藏的线性层之前，我们必须reshape（）或展平我们的张量。每当我们将卷积层的输出作为线性层的输入传递时，都是这种情况。

由于第四层是第一线性层，因此我们将整形操作作为第四层的一部分。

# (4) hidden linear layer
t = t.reshape(-1, 12 * 4 * 4)
t = self.fc1(t)
t = F.relu(t)

# (5) hidden linear layer
t = self.fc2(t)
t = F.relu(t)

我们在CNN权重的帖子中看到，整形操作中的数字12由来自前一个卷积层的输出通道数确定。

但是，4 * 4仍然是一个悬而未决的问题。让我们现在揭示答案。 4 * 4实际上是12个输出通道中每个通道的高度和宽度。

我们从1 x 28 x 28输入张量开始。这样就给出了一个单一的彩色通道，即28 x 28的图像，并且当我们的张量到达第一线性层时，尺寸已经改变。

通过卷积和合并操作，将高度和宽度尺寸从28 x 28减小到4 x 4。

卷积和池化操作是对高度和宽度尺寸的归约操作。我们将在下一篇文章中看到这是如何工作的，并看到计算这些减少量的公式。现在，让我们完成实现此forward（）方法。

张量重塑后，我们将展平的张量传递给线性层，并将此结果传递给relu（）激活函数。

Output Layer #6

我们网络的第六层也是最后一层是线性层，我们称为输出层。当我们将张量传递到输出层时，结果将是预测张量。由于我们的数据具有十个预测类别，因此我们知道我们的输出张量将具有十个元素。

# (6) output layer
t = self.out(t)
#t = F.softmax(t, dim=1)

十个组件中的每个组件内的值将对应于我们每个预测类的预测值。

在网络内部，我们通常使用relu（）作为我们的非线性激活函数，但是对于输出层，只要我们有一个要预测的类别，我们就使用softmax（）。 softmax函数针对每个预测类返回正概率，并且概率之和为1。

但是，在本例中，我们不会使用softmax（），因为我们将使用的损失函数F.cross_entropy（）在其输入上隐式执行softmax（）操作，因此我们只返回的结果。最后的线性变换。

这意味着我们的网络将使用softmax操作进行训练，但是在训练过程完成后，当网络用于推理时，无需计算其他操作。

Conclusion

大！ 我们做到了。 这就是我们在PyTorch中实现神经网络转发方法的方式。

def forward(self, t):
    # (1) input layer
    t = t

    # (2) hidden conv layer
    t = self.conv1(t)
    t = F.relu(t)
    t = F.max_pool2d(t, kernel_size=2, stride=2)

    # (3) hidden conv layer
    t = self.conv2(t)
    t = F.relu(t)
    t = F.max_pool2d(t, kernel_size=2, stride=2)

    # (4) hidden linear layer
    t = t.reshape(-1, 12 * 4 * 4)
    t = self.fc1(t)
    t = F.relu(t)

    # (5) hidden linear layer
    t = self.fc2(t)
    t = F.relu(t)

    # (6) output layer
    t = self.out(t)
    #t = F.softmax(t, dim=1)

    return t

下一个见！