2021年hznu寒假集训第四天 搜索入门
2021年hznu寒假集训第四天
前言
和树的遍历类似,图的遍历也是从图中某点出发,然后按照某种方法对图中所有顶点进行访问,且仅访问一次。
但是图的遍历相对树而言要更为复杂。因为图中的任意顶点都可能与其他顶点相邻,所以在图的遍历中必须记录已被访问的顶点,避免重复访问。
根据搜索路径的不同,我们可以将遍历图的方法分为两种:广度优先搜索和深度优先搜索。
图的加边与遍历
法1
vector<int>G[N];
//x->y
void way1(){
G[x].push_back(y);//加边方式
int sz=G[x].size();//遍历方式
for(int i=0;i<sz:i++){
int to=G[x][i];
}
}
法2:链式前向星
int tot,ver[N<<1],Next[N<<1],head[N];
//tot标号,ver[]存储每个编号的边连出去的点,Next[]忘前连接的边的编号,head[]最后一个编号的边
void add(int u,int v){
//添加一条从u->v的边
++tot;ver[tot]=v;
Next[tot]=head[u];head[u]=tot;
}
void way2(){
add(x,y);//加边方式
for(int i=head[x];i;i=Next[i]){
//遍历方式
int to=ver[i];
}
}
输入
#define pii pair深度优先搜索(DFS)
以深度优先,可以理解为一条路走到黑
迷宫求解是否可达问题
连通块数求解
有根树的深度,树的重心,图的划分,tarjan算法,树的dfs序等
dfs迷宫可达问题

dfs问题常与递归函数关联
用函数bool dfs(int x,int y)来表示从点(x,y)出发是否可以到达终点,可行则返回1,否则为0
#includedfs连通块数量求解
油井(HDU-1241)
通过上一题应该有所启发,我们只需要在主函数中遍历虽有点,对每个没有访问过的@点进行一个dfs将其能到达的所有点都标记掉,
那么连通块的数量就是我们主函数里调用了多少次dfs函数。
Counting Sheep (HDU - 2952)
#include 广度优先搜索(BFS)
广度优先,层次遍历,一层一层扩展
可以理解为分身术,我妈安排我买东西,我到了超市,使用分身术,分别去买油,买盐,买菜
搜索策略
优先搜索距源点所在的0层,在搜索第1层,在搜索第2层,……直到所有节点均搜索完毕
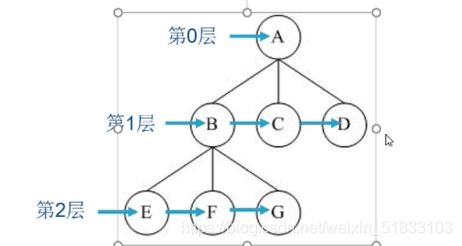
实现方式
通常采用STL容器中的队列queue实现,先进先出。
bfs是按照层序遍历的,如前面的ppt,只有当一层状态完全扩展完毕,才会进入下一层
我们将bfs和dfs 的遍历路径对比一下

bfs:ABCDEFG
dfs:ABEFGCD
我们先抛开记录路径这一说,只考虑如何使路径最短。
按照层序遍历的思想,是不是如果有一个状态先前出现过了,之后再出现的话花费的代价一定比之前的大,
因为先前的状态在搜索树中的层更偏上一点。
所以我们开一个bool vis[][]来记录这个状态有没有出现过,减少搜索规模也同时保证答案的正确性。
一个(x.y)的点可以向上下左右各扩展一次,花费代价均为1,所以我们对于每个点都尝试进行四个方向的扩展.
最终就一定能遍历到终点。
而且根据答案最优性,一个状态最优是不是保证他被较前的一个状态扩展到便可行。
所以当一个(x2.y2)被(x1.y1)扩展到的时候,我们记录他的步数等于step[x2][y2]=step[x1][y1]+1.
一个点只被有效入队一次,有效出队一次,有n*n个点,复杂度便是O(n*n).
Find a way
#include二分图染色
二分图定义:
二分图也称二部图,是图论里的一种特殊模型,也是一种特殊的网络流。其最大的特点在于,可以将图里的顶点分为两个集合,且集合内的点没有直接关联,如下图所示。
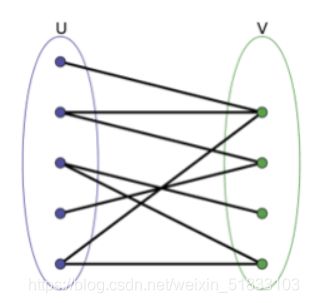
判断二分图的常见方法是染色法:用两种颜色,对所有顶点逐个染色,且相邻顶点染不同的颜色,如果发现相邻顶点染了同一种颜色,就认为此图不为二分图。 当所有顶点都被染色,且没有发现同色的相邻顶点,就退出。
dfs解法:
解法一: dfs
经典思路:dfs返回一个boolean值,DFS的含义是:给当前节点(draw[index])染成color是否合法
* 如果已经染色,就检查是否是要涂的color
* 如果还未染色,就涂上color,并给其所有邻居尝试染上反色(递归)
#include 解法二:BFS
经典思路:每次出队时,就判断出队节点的邻居是否被染色:
* 如果未被染色,就染成出队节点的反色
* 如果已经染色,就检查邻居的颜色是否合法,即与出队节点互为反色
#include 解法3 并查集
很有趣的思路:我们把一个节点的所有邻居合并到一个集合里————“敌人的敌人就是朋友”
*
* 代码思路:直接for遍历graph,每次遍历一个节点,以其为中心扫描邻居:
* 如果中心节点与邻居在同一集合,直接返回false
* 否则连接所有的邻居
public boolean isBipartite(int[][] graph) {
int len = graph.length;
UnionSet unionSet = new UnionSet(len);
for (int i = 0; i < len; i++) {
int[] js = graph[i];
for (int j : js) {
if (unionSet.isUnion(i, j)) {
return false;
}
unionSet.union(j, js[0]);
}
}
return true;
}
}
class UnionSet {
int[] roots;
public UnionSet(int len) {
roots = new int[len];
for (int i = 0; i < len; i++) {
roots[i] = i;
}
}
public int findRoot(int node) {
// fintRoot寻找根节点是并查集的核心。
if (node == roots[node]) {
// 实际上这种递归写,寻找根节点的同时压缩了树的路径
return node;
}
roots[node] = findRoot(roots[node]);
return roots[node];
}
public boolean isUnion(int node1, int node2) {
return findRoot(node1) == findRoot(node2);
}
public void union(int node1, int node2) {
roots[node1] = findRoot(node2);
}
}
换壳题
【可能的二分法】
给定一组 N 人(编号为 1, 2, …, N), 我们想把每个人分进任意大小的两组。
每个人都可能不喜欢其他人,那么他们不应该属于同一组。
形式上,如果 dislikes[i] = [a, b],表示不允许将编号为 a 和 b 的人归入同一组。
当可以用这种方法将每个人分进两组时,返回 true;否则返回 false。
示例 1: 输入:N = 4, dislikes = [[1,2],[1,3],[2,4]] 输出:true
示例 2: 输入:N = 3, dislikes = [[1,2],[1,3],[2,3]] 输出:false
示例 3: 输入:N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]] 输出:false
>>> 两个互相不喜欢的人?
>>> 你会发现,这与"不和睦的邻居"是完全一类的问题————保证相邻节点不能同色。
>>>
>>> 可是,无论是"从某个点出发开始BFD/DFS整个图的染色法", 还是"将某个点的所有敌人都连接起来的并查集",用此时的dislikes数组,都是很难实现的
>>> 我们需要对dislikes数组进行处理————转换为邻接的形式。
>>> 下面给出两种转换方式:
List<Set<Integer>> list = new ArrayList<>();
for(int i = 0; i < N + 1; i++){
list.add(new HashSet<>());
}
for(int[] dislike : dislikes){
list.get(dislike[0]).add(dislike[1]);
list.get(dislike[1]).add(dislike[0]);
}
Map<Integer, List<Integer>> map = new HashMap<>();
for(int i = 0; i < N + 1; i++){
map.put(i, new ArrayList<>());
}
for(int[] dislike : dislikes){
map.get(dislike[0]).add(dislike[1]);
map.get(dislike[1]).add(dislike[0]);
}
// 因为学生编号从1开始,我们假设有一个0的同学————他谁都不讨厌。 他丝毫不会影响最终结果。理解一下。
// 考虑到连通域不止一个的问题,BFS/DFS染色时依旧要从每个节点都尝试开始一次
拓扑排序
它是对有向图的顶点排成一个线性序列。
至于定义,百科上是这么说的:
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边
一些其他注意:
DGA:有向无环图
AOV网:数据在顶点 可以理解为面向对象
AOE网:数据在边上,可以理解为面向过程!
而我们通俗一点的说法,就是按照某种规则将这个图的顶点取出来,这些顶点能够表示什么或者有什么联系。
规则:
图中每个顶点只出现一次。
A在B前面,则不存在B在A前面的路径。(不能成环!!!!)
顶点的顺序是保证所有指向它的下个节点在被指节点前面!(例如A—>B—>C那么A一定在B前面,B一定在C前面)。所以,这个核心规则下只要满足即可,所以拓扑排序序列不一定唯一!
拓扑排序算法分析
从DGA图中找到一个没有前驱的顶点输出。(可以遍历,也可以用优先队列维护)
删除以这个点为起点的边。(它的指向的边删除,为了找到下个没有前驱的顶点)
重复上述,直到最后一个顶点被输出。如果还有顶点未被输出,则说明有环!
对于上图的简单序列,可以简单描述步骤为:
1:删除1或2输出

2:删除2或3以及对应边

3:删除3或者4以及对应边

3:重复以上规则步骤

这样就完成一次拓扑排序,得到一个拓扑序列,但是这个序列并不唯一!从过程中也看到有很多选择方案,具体得到结果看你算法的设计了。但只要满足即是拓扑排序序列。
拓扑排序代码实现
我们具体的代码思想为:
1.新建node类,包含节点数值和它的指向(这里直接用list集合替代链表了)
2.一个数组包含node(这里默认编号较集中)。初始化,添加每个节点指向的时候同时被指的节点入度+1!(A—>C)那么C的入度+1;
3.扫描一遍所有node。将所有入度为0的点加入一个栈(队列)。
4.当栈(队列)不空的时候,抛出其中任意一个node(栈就是尾,队就是头,顺序无所谓,上面分析了只要同时入度为零可以随便选择顺序)。将node输出,并且node指向的所有元素入度减一。如果某个点的入度被减为0,那么就将它加入栈(队列)。
5.重复上述操作,直到栈为空。
这里主要是利用栈或者队列储存入度只为0的节点,只需要初次扫描表将入度为0的放入栈(队列)中。
6.这里你或许会问为什么。
因为节点之间是有相关性的,一个节点若想入度为零,那么它的父节点(指向节点)肯定在它为0前入度为0,拆除关联箭头。从父节点角度,它的这次拆除联系,可能导致被指向的入读为0,也可能不为0(还有其他节点指向儿子)
package 图论;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
public class tuopu {
static class node
{
int value;
List<Integer> next;
public node(int value) {
this.value=value;
next=new ArrayList<Integer>();
}
public void setnext(List<Integer>list) {
this.next=list;
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
node []nodes=new node[9];//储存节点
int a[]=new int[9];//储存入度
List<Integer>list[]=new ArrayList[10];//临时空间,为了存储指向的集合
for(int i=1;i<9;i++)
{
nodes[i]=new node(i);
list[i]=new ArrayList<Integer>();
}
initmap(nodes,list,a);
//主要流程
//Queueq1=new ArrayDeque();
Stack<node>s1=new Stack<node>();
for(int i=1;i<9;i++)
{
//System.out.print(nodes[i].next.size()+" 55 ");
//System.out.println(a[i]);
if(a[i]==0) {
s1.add(nodes[i]);}
}
while(!s1.isEmpty())
{
node n1=s1.pop();//抛出输出
System.out.print(n1.value+" ");
List<Integer>next=n1.next;
for(int i=0;i<next.size();i++)
{
a[next.get(i)]--;//入度减一
if(a[next.get(i)]==0)//如果入度为0
{
s1.add(nodes[next.get(i)]);
}
}
}
}
private static void initmap(node[] nodes, List<Integer>[] list, int[] a) {
list[1].add(3);
nodes[1].setnext(list[1]);
a[3]++;
list[2].add(4);list[2].add(6);
nodes[2].setnext(list[2]);
a[4]++;a[6]++;
list[3].add(5);
nodes[3].setnext(list[3]);
a[5]++;
list[4].add(5);list[4].add(6);
nodes[4].setnext(list[4]);
a[5]++;a[6]++;
list[5].add(7);
nodes[5].setnext(list[5]);
a[7]++;
list[6].add(8);
nodes[6].setnext(list[6]);
a[8]++;
list[7].add(8);
nodes[7].setnext(list[7]);
a[8]++;
}
}
