Python编程基础与应用（陈波著）微实践

微实践1——鸡兔同笼

有若干只鸡兔同在一个笼子里，从上面数，有35个头，从下面数，有94只脚。问笼中各有多少只鸡和兔？

解决方案：

iHead = 35
iFeet = 94
a = iFeet - iHead*2
iRabbits = a/2
iChicken = iHead - iRabbits
print("兔兔有{:.0f}只，小鸡有{:.0f}只".format(iRabbits,iChicken))

输出：

兔兔有12只，小鸡有23只

format格式化函数

print("我的爱人是{name},他最大的特点是{factor}".format(name='wjy',factor='可爱'))
lover = {
     'name':'wjy','factor':'可爱'}
print("我的爱人是{name},他最大的特点是{factor}".format(**lover))##注意**
mylittleone = ['wjy','可爱']
print("我的爱人是{0[0]},他最大的特点是{0[1]}".format(mylittleone))
#注意0指代第一个列表，[0]指代第一个元素
number1 = 3.352342352
print('{:.2f}'.format(number1))
print("{:.0f}".format(number1))
print("{:+.2f}".format(number1))
print("{:.3%}".format(number1))
number2 = -3.614134
print("{:+.0f}".format(number2))#加号是指显示符号.保留整数时四舍五入
number3 = 9
print("{:0>5d}".format(number3))
print("{:x<10d}".format(number3))
print("{:>10d}".format(number3))#右对齐，宽度为10
print("{:<10d}".format(number3))#左对齐
print("{:^10d}".format(number3))#居中对齐
print("{:b}".format(number3))#2
print("{:d}".format(number3))#10
print("{:o}".format(number3))#8
print("{:x}".format(number3))#16

print("{
     {:2.f}}".format(number3))#在有format函数的语句中，{}可以转义{}

输出

我的爱人是wjy,他最大的特点是可爱
我的爱人是wjy,他最大的特点是可爱
我的爱人是wjy,他最大的特点是可爱
3.35
3
+3.35
335.234%
-4
00009
9xxxxxxxxx
         9
9
    9
1001
9
11
9
{
     :2.f}

微实践2—地球时间

现代计算机内部均安装有RTC（ Real Time Clock芯片或者其CPU具备RTC功能。RTC芯片内部有一个计数器，通常用于记录从GMT时间（格林尼治时间）1970年1月1日零时起，总共流逝的Tick（滴答）个数。
RTC芯片会按照固定的节拍增加这个计数器的值，以达到计时的目的。至于一个Tick是何种精度，则取决于计算机的工作频率及RTC的能力，大部分都在微秒级。RTC芯片工作是需要消耗电能的，那么计算机断电时计时会停止吗？不会，读者可以在自己的计算机主板甚至手机主板上找到用于给RTC供电的纽扣锂电池。
有的读者可能还会想到，北京和东京分处不同时区，计算机显示日期时间时是否还需进行时区转换呢？
是的，在操作系统中可以设置时区，设置完成后，操作系统会自动完成从RTC内部计数器计数值到特定时区的时间转换。顺便提一句，现代计算机大部分会连网，在连上 Internet时，操作系统很可能会自动从网上刷新时间，以消除RTC的计时误差。

#earthtime.py
#打印系统当前的格林尼治时间
import time 
curTime = time.time()
totalSeconds = int(curTime)
curSeconds = totalSeconds % 60
totalMinutes = totalSeconds // 60
curMinutws = totalMinutes % 60
totalHours = totalMinutes//60
curHours = totalHours % 24
print("现在的格林尼治时间为{
     }时{
     }分{
     }秒，自1970年1月1日开始\
已经经历了{
     }秒".format(curHours,curMinutws,curSeconds,totalSeconds))

#打印系统时间
import datetime
curDate = datetime.datetime.now()
print("{}-{}-{}\n{}:{}:{}".format(curDate.year,curDate.month\
,curDate.day,curDate.hour,curDate.minute,curDate.second))

• 对象.属性名
• 对象.函数名()

微实践5—抓扑克牌的手气

扑克是流行全世界的一种纸牌。一副扑克牌有54张牌，其中52张是正牌，另2张是副牌（大王和小王）。52张正牌又均分为13张1组，共有黑桃、红桃、梅花、方块四组。每组花色的牌包括从2-10以及A、」、Q、K标示的13张牌。在比较流行的斗地主游戏中，三个玩家中除庄家外，另外两个玩家一人要拿17张牌。如果洗牌过程是完美的，那么对于一个玩家而言，拿到哪十七张牌是完全随机的下述程序首先生成了54张扑克牌，然后借助于随机数从中抽取17张牌。

#poker.py
import random
suits = ['Spades','Hearts','Diamonds','Clubs']
ranks = ['A','2','3','4','5','6','7','8',\
    '9','10','J','Q','K']
cards = [x+'_'+y for x in suits for y in ranks]
cards += ['Red Joker','Black Joker']
random.shuffle(cards)
cardsHold = []
for x in range(17):
    c = random.choice(cards)
    cardsHold.append(c)
    cards.remove(c)
print("Your cards are: ",', '.join(cardsHold))

输出

Your cards are:  Hearts_8,Diamonds_10,Clubs_A,Diamonds_7,Spades_10,Spades_A,Clubs_7,Red Joker,Diamonds_9,Hearts_J,Hearts_Q,Hearts_5,Diamonds_2,Spades_Q,Spades_2,Diamonds_5,Hearts_10

• random库

#random库
import random
#random.seed() 会改变随机生成器的种子；传入的数值用于指定随机数生成时
# 所用算法开始时所选定的整数值，如果使用相同的seed()值，则每次生成的随机数都相同；
# 如果不设置这个值，则系统会根据时间来自己选择这个值，此时每次生成的随机数会因时间的差异而有所不同。
random.seed(928)
for i in range(6):
    if i != 5:
        print(random.randrange(10),end=',')
    else:
        print(random.randrange(10))
random.seed(512)
for i in range(6):
    if i != 5:
        print(random.randrange(10),end=',')
    else:
        print(random.randrange(10))

#randint(a, b)	生成一个[a, b]之间的整数
random.seed()#前面设置了random.seed(512),如果不重置，会产生固定的随机数831
print(random.randint(512,928))

#randrange(m, n[, k])	生成一个[m, n)之间以k为步长的随机整数
print(random.randrange(512,928,31))

#getrandbits(k)	生成一个k比特长的随机整数
#注意最大数字为2**(k-1)+2**(k-2)+……+2**0
print(random.getrandbits(6))

#uniform(a, b)	生成一个[a, b]之间的随机小数
print(random.uniform(512,928))

# choice(seq)	从序列seq中随机选择一个元素
my_list = ['大海','宇宙','人世间','肉体','创造','苦难','甘甜','微涩']
print(random.choice(my_list))

#shuffle(seq)将序列seq中元素随机排列，返回打乱后的序，是改变原来的序列
random.shuffle(my_list)
print(my_list)

输出

4,6,8,2,2,7
0,7,2,5,6,5
802
791
58
554.2117800479772
人世间
['苦难', '甘甜', '人世间', '宇宙', '创造', '肉体', '大海', '微涩']

微实践6—我的幸运数

数字命理学家"认为能够基于名字的"数值"来找到一个人的幸运数字。幸运数字等于名字中各字母的值之和。其中，“a"的值为1，"b的值为2，”c"的值为3，…z的值为26.运行下述程序，输入一个中间不包含空格的英文名字，程序将计算出一个幸运数

#Luckynumber.py
lname = list(input("Do you want to know your luckynumber?\n\
    please tell me your name:").lower().strip().replace(' ',''))
luckynumber = 0
for x in lname:
    luckynumber += ord(x)-96
print("Your lucknumber is: ",luckynumber)

输出

Do you want to know your luckynumber?
    please tell me your name:wangjunyi
Your lucknumber is:  124

• ascii码

#ASCII码转换
sword = input("请输入你想转换为ASCII码的字符：")
inumber = int(input("请输入ASCII码值，看看它是什么:"))
print(ord(sword))
print(chr(inumber))

输出

请输入你想转换为ASCII码的字符：a
请输入ASCII码值，看看它是什么92
97
\

微实践7—滚雪球的复利

人生就像滚雪球，最重要的是发现很湿的雪和很长的坡。–巴菲特投神所说的很湿的雪，是指投资的本金；而很长的坡，则是一个重要的财富秘诀-复利。复利即通常所说的利滚利，也就是把上一轮投资所得的本金和利息，作为下一轮投资的本金。复利对于投资者或者放贷人而言，非常有利，看似非常小的投资倣放贷收益，经过时间的累积，可以获得成倍的增长。但对于借款人而言，就不那么美好了。歌剧《白毛女》中，杨白劳就是因为欠下了"驴打滚"的债，利滚利还不起，才被迫失去了喜儿。
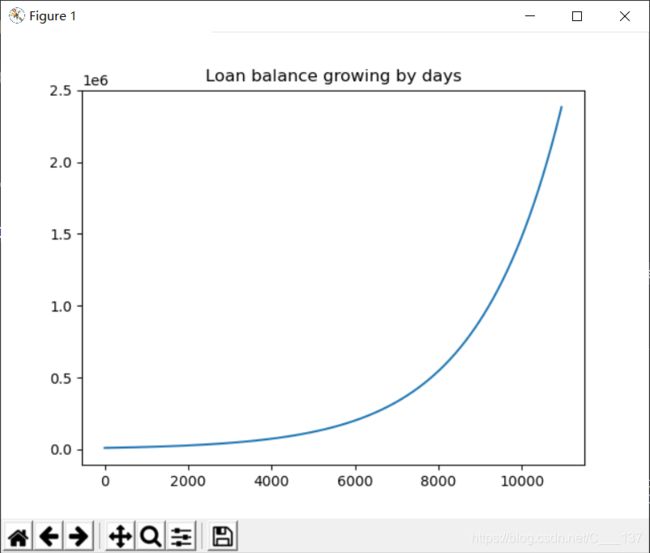
假设某位同学，从某贷款公司借款10000元，约定日利率为万分之五，按日计复利。如果这位同学一直没有还钱，那么30年后，他欠对方多少钱？

#loan.py
fBalance = 10000
fInterest = 5/10000
balances = []
for x in range(30*365):
    fBalance *= (1+fInterest)
    balances.append(fBalance)

from matplotlib import pyplot as plt 
plt.plot([x for x in range(30*365)],balances)
plt.title('Loan balance growing by days')
plt.show()

输出

2383241.4624957815

• matplotlib库，详情见文章

微实践8—发现圆周率

在边长为2的正方形内有一个直径为2半径为1的内切圆。根据圆的面积公式，内切圆的面积s=Tr由于r=1，所以m=内切圆的面积。边长为2的正方形面积为4.在已知正方形的面积为4的情况下，如何求得内切圆的面积呢？布冯提出了投针的方法。假设10000根针"均匀随机“地垂直落在正方形上，每根针在正方形上形成一个“投点。那么落入圆内的投点数量与圆的面积正相关：

#picalc.py
import random
icircle = 0
N = 1000000
for times in range(N):
    x = random.uniform(-1,1)
    y = random.uniform(-1,1)
    if x**2+y**2 <= 1:
        icircle += 1
print("Π =",4 * icircle / N)

微实践10—九层之台，起于累土

九层之台，起于累土"出自春秋楚·李耳《老子》第64章：“合抱之木，生于毫末；九层之台，起于累土；千里之行，始于足下”。不论起点有多低，只要不断成长，假以时日，终有所成一张厚度为0.1毫米的足够大的纸，每对折一次，厚度翻倍。问：这张纸对折多少次以后将达到世界最高峰珠穆朗玛峰的高度？如果凭直觉，作者觉得再怎样也要上千次对折才行。

#everest.py
iCounter = 0
fthick = 0.1e-3
while fthick < 8848:
    fthick *= 2
    iCounter += 1
print("对折{}次后，纸的厚度超过了珠穆朗玛峰".format(iCounter))

输出

对折27次后，纸的厚度超过了珠穆朗玛峰

微实践11-冒泡排序

当水里有气泡时，气泡的密度比水小，水的浮力大于气泡的重力，上浮。而水面的石头则注定下沉。冒泡排序（ bubble
sort即得名于此。请注意，这里的所谓浮、沉、轻和重只是形象化的描述，不要机械理如下图中的9个整数所构成的序列。现在我们要进行非递减，也就是递增排序。我们从前（下标0往后两两比较，如果左边的元素大于右边的元素，则两两交换。如下例，9与3比较，9>3，交换；9与1比较，
9>1，交换；9与4比较，9>4，交换…最后9与5比较，9>5，交换。经过这一轮共8次的两两比较以及次数不确定的交换，我们发现，序列中最大的那个元素9到了序列的尾部，即下标8的位置。而这个位置正好是元素9在排序后的目标位置。

#Bubblesort.py
seq = [eval(x)for x in input("请输入多个整数，用空格隔开").split( )]
for i in range(len(seq)-1):#i表示第i+1次进行排序，此时后面有已经排好的元素i个，一共需要排列len(seq)-1次
    for j in range(len(seq)-i-1):#j表示针对第i次排列，从索引为0的元素开始，一共比较len(seq)-i-1次
        if seq[j] > seq[j+1]:
            seq[j],seq[j+1] = seq[j+1],seq[j]
print("我整理好啦！") 
print(seq)
 

微实践12—新浪和新娘穷举

有3对新郎和新娘参加集体婚礼，三个新郎为A、B、C，3个新娘为X、Y、Z。婚礼的主持人一时间忘了谁应该和谁结婚。于是询问参加婚礼的6个人的3个，得到如下回答：
回答
-新郎A说他将和新娘X结婚
-新娘X说她将和新郎C结婚
-新郎C说他将和新娘Z结婚。
从3个人回答问题的表情推测，上述回答都是在开玩笑，即都是假的。问题：如果上述三个回答都是假的，找出谁和谁结婚的真相。
至少到目前，我们还很难说计算机比人类聪明。相对于人脑，计算机有一个天生的优势，那就是快。对于组合数不是太多的问题，程序可以列举全部的可能组合，然后逐一检查和确认。这种方法，称之为穷举法，也叫暴力求解法- brute force

#Marriage.py
brides = ['X','Y','Z']
bridegrooms = ['A','B','C']
for a in bridegrooms:
    for b in bridegrooms:
        for c in bridegrooms:
            if a!=b and a!=c and c!=b and\
                a != 'A' and a != 'C' and c != 'C':
                print("They are: {}_X, {}_Y, {}_Z".format(a,b,c))

• 自己做的版本并不是很好，是没有顺序地罗列了全部的情况，最后不会写出三对没有重复人出现的配偶了。
• 这里将新娘当作已知的顺序：X, Y, Z，然后将新郎逐个配对，用三重循环找出！=的情况

微实践13-存世作品最多的唐代诗人

李杜文章在，光焰万丈长"。说起唐诗和唐代诗人，很多人的第一反应是李白和杜甫。就名头来说，李杜最响。但谁的诗作最多呢？如果说写作数量，估计不可考。但仅就存世诗作而言，还是可以统计的。在本章的项目目录下有一个名为 gts_zht. txt的文本文件，共收录唐诗4万多首。格式如下：

128_65 哭孟浩然 王縫 故人不可見，漢水日東流。借問襄陽老，江山空蔡州

可以看见，文本文件的每一行是一首唐诗，用空格可分为四个部分，从前至后分别是：编号，题名，作者，全文。下述代码统计了毎位作者的存世诗作数量，并打印了存世作品数量最多的十位作者。

#Poemscount.py
f = open('qts_zht.txt','r',encoding='UTF-8')
list_lines = f.readlines()#注意f.readlines()返回的是列表，列表的每一个元素都是一行（str）
dictpoets = {
     }
lstpoets = []
for i in list_lines:
    poem = i.split( )
    dictpoets[poem[2]] = dictpoets.get(poem[2],0) + 1#注意这里的表达，
#get()依然只是返回值而已，要么返回0，要么返回poem[2]这个键的值
for k,v in dictpoets.items():
    lstpoets.append([k,v])

lstpoets.sort(key = lambda x:x[1],reverse = True)
print(lstpoets[:15])

• lambda()

#lambda函数
g = lambda x:x+1#相当于函数中的转换关系f
print(g(1))
#应用：

#sort(key = lambda x:)
list1 = [['三体',1],['星际穿越',12],['泰坦尼克号',0],['肖申克的救赎',4]]
list1.sort(key = lambda x:x[1],reverse = True)
print(list1)

#map()
#第一个参数 function 以参数序列中的每一个元素调用 function 函数，返回包含每次 function 函数返回值的新列表。
#map(function, iterable, ...)
mapResult = map(lambda x : x[1]*2 ,list1)#注意map返回的是迭代器！
print(mapResult)
print(list(mapResult))#注意map的返回值，不是全部列表，而是你的lambda作用的
print(list1)#map不改变原有seq

#filter()过滤器
list1 = [1,4,3,5,7,2,9,22,11,4,2,6,78,53]
filterResult = filter(lambda x:x % 3 == 0,list1) #返回可迭代对象
print(filterResult)
print(list(filterResult))

输出

2
[['星际穿越', 12], ['肖申克的救赎', 4], ['三体', 1], ['泰坦尼克号', 0]]
<map object at 0x00000227E52B5790>
[24, 8, 2, 0]
[['星际穿越', 12], ['肖申克的救赎', 4], ['三体', 1], ['泰坦尼克号', 0]]
<filter object at 0x00000227E52B5E50>
[3, 9, 6, 78]

微实践15-一对兔兔和函数的增长

数学家列昂纳多·斐波那契研究了野外兔子的繁殖问题：一般而言，兔子出生两个月后，就有繁殖能力假设一对兔子每个月能生出一对小兔子而且所有兔子都不死。如果现在往一片没有兔子的新大陆上放生一对新生的兔子，那么一年以后那个大陆上有多少只兔子？两年以后呢？
第1个月，那对兔子还没有繁殖能力，仍为幼兔。故幼免数量为1对，成兔数量为0对，总对数为1；第2个月，那对兔子性成熟，变成成兔。故幼兔数量为0对，成兔数量为1对，总对数为1第3个月，2月时的成兔1对，生了1对小兔子，故幼兔1对，成兔1对，总对数为2第4个月，3月时的成兔1对生了1对小兔子，且3月时的幼兔1对变成了成免，故幼免数量为1对，成兔变成了2对，总对数为3

#Fibl.py
#所谓递归，都可以想成类似于f(x) = f(x-1)+f(x-2), x=somerange
def fibonacci(n):
    if n == 1 or n == 2:
        return 1
    a,b = 1,1
    for x in range(3,n+1):#注意这里对递归的转义表达
        c = a+b
        a,b = b,c
    return c
        
# months = int(input("你想看前多少个月的兔兔增长？："))
# for x in range(1,months+1):
#     print('经过{}个月，兔兔已经{}只啦！'.format(x,fibonacci(x)))

#比较Fibonacci和n^2、n^3的增长速度
def main():
    y_fibl = []
    y_n2 = []
    y_n3 = []
    x = [x for x in range(1,25)]
    for i in x:
        f = fibonacci(i)
        y_fibl.append(f)
        y_n2.append(i**2)
        y_n3.append(i**3)

    from matplotlib import pyplot as plt
    plt.plot(x,y_fibl,color = 'black',label = '$y = fibonacci(x)$')
    plt.plot(x,y_n2,linestyle = '-',color = 'red',label = '$y = x**2$')
    plt.plot(x,y_n3,linestyle = '--',color = 'orange',label = '$y = x**3$')
    plt.legend()
    plt.show()

main()

输出

微实践16—分治法寻找假硬币

有一堆共η枚硬币，其中一枚是假币，外观上无法区分，只知道假币的重量稍轻。要求仅使用一个天平，使用最少的重量比较次数找出假硬币。
最简单的方法是把硬币编号，然后
（1）。使用天平比较第1枚硬币与第2枚硬币的重量。如果天平失衡，轻者为假，否则继续。
（2）。使用天平比较第1枚硬币与第3枚硬币的重量。如果天平失衡，轻者为假，否则继续。
（n-1）。使用天平比较第1枚硬币与第η枚硬币的重量。如果天平失衡，轻者为假，否则未发现假币在最坏情况下，需要进行η-1次重量比较，才能找出假硬币。
分治法有助于提高査找效率。将η个硬币分成数量相同的两堆，如果η为偶数，每堆的硬币个数为η/2；如果n为奇数，每堆的硬币个数为（η-1）/2，两堆之外还会剩余一个硬币。将两堆硬币上天平比较重量，如果有一堆较轻，那么假的硬币必然在轻的那一堆中。如果两堆硬币重量相等，且两堆之外有一个剩余硬币，则那个剩余硬币就是假硬币。如果两堆硬市重量相等，且两堆之外没有剩余硬币，则查找任务失败，未发现假硬币。
我们把硬币的个数η视为寻找假硬币问题的规模，显然η越大，需要比较重量的次数就越多。可以看到，即便是在最坏的情况下，每次比重，必然能将假硬币定位到数量约为η/2的硬币中。即，每比较一次，问题的规模缩小一半。使用上述分治法，最坏情况下，我们只需要 log2n次比重，即可找出假硬币，

#Falsecoin.py
def falsecoin(seq,istart,iend,idx = 0):
    #创建一个函数根据某序列seq，从istart开始到iend结束，idx为它在序列中的位置
    n = len(seq[istart:iend])
    a = n//2 
    wl = sum(seq[istart:a+istart])
    wr = sum(seq[len(seq)-a:iend])
    if wr == 0:
        return istart + a
    elif wl == 0:
        return istart + 1
    elif wl < wr:
        iend = a + istart #这里出现bug：iend = a 
        return falsecoin(seq,istart,iend,idx)
    elif wl > wr:
        istart = a
        iend = len(seq)
        idx = a
        return falsecoin(seq,istart,iend,idx)
    elif wl == wr:
        return idx + a

def main():
    coins = [1,1,1,0,1,1,1]
    n = len(coins)
    index = falsecoin(coins,0,n)
    print("哦豁，它在第{}个".format(index+1))

main()