机器学习理论篇之线性回归（python实现）

1. 线性回归模型：（M个样本，n个特征值，一个bias）

矩阵化表现形式：

注意这里采用的XW的向量表示形式，如果要采用W（T）X的形式X矩阵的向量表现形式就不一样了。

其实机器学习的目的就是要求出最优的W参数值，因此我们需要用到损失函数。

2.损失函数（cost）：

  最小二乘法表示损失函数：

      何为最小二乘法，其实很简单。我们有很多的给定点，这时候我们需要找出一条线去拟合它，那么我先假设这个线的方程，然后把数据点代入假设的方程得到观测值，求使得实际值与观测值相减的平方和最小的参数。

M是样本数量，就是我们训练样本的数量。如果每一个样本单独求损失函数的话，最后要求和才是整个模型的损失函数

如果是用向量矩阵求损失函数的话，所有样本全部代入，直接求出来的是一个值，就是模型的损失函数。

注意：上面的两个大小写y实际上是同一个y，都是样本真实值的向量，是M×1维的向量矩阵

分析一下：向量矩阵的维度：

X 是M×（n+1）维

W是（n+1）×1维

XW是 M×1维

y是M×1维

我们的目的就是要使损失函数最小，然后求出损失函数最小的W，这时候我们求最小损失函数有两种情况：

3.学习过程：求出损失函数最小的W

 a.矩阵满秩时求解：（Normal Equation）

直接令J（w）的导数等于0，求出最小的w。

此时直接将向量矩阵X和y代人上面的方程式即可。

分析一下向量维度：

X是M×（n+1）维

X(T)是 （n+1）×M维

X(T)X是 （n+1）×（n+1）维

y是M×1维

X（T）y是（n+1）×1维

W是（n+1）×1维==[（n+1）×（n+1）][(n+1)×1]

b.当矩阵不满秩时：(梯度下降法)

梯度下降算法是一种求局部最优解的方法，对于F(x)，在a点的梯度是F(x)增长最快的方向，那么它的相反方向则是该点下降最快的方向。

注意梯度下降法只适合与求解损失函数是凸函数（Convex Function）的问题。

算法思路：

1）首先对w赋值，这个值可以是随机的，也可以让w是一个全零的向量。

2）改变w的值，使得J(w)按梯度下降的方向进行减少。

描述一下梯度减少的过程，对于我们的函数J(w)求偏导J：

这里图片上的θ就是我们上面所说的W不要弄混。

Repeat  until convergence：{

}

注意：上面的α表示的是学习率，学习率的选择通常是 ....0.001,  0.003,  0.01,  0.03,    0.1, 0.3, 1....这种方式。

注意：上面的θ更新时应该同步，因为我们有很多的θ是要同时更新的，一般解决办法是，先把更改后的θ保存为一个临时temp值，等所有的θ更新完之后，在一块赋值给原θ

分析一下向量维度：

如果是单个样本进行更新的话，每个维度都是1，没什么好解释的。

下面分析一下用多个样本的维度：

h（x）是M×1维

y是M×1维

E=h（x）-y是M×1维

X(T)是（n+1）×M

注意：在进行梯度下降算法之前，最好对样本特征值，进行Feature Scaling

Feature Scaling 确保样本的特征取值都在一个相似的范围之内，尽量保证在-1～1之间的范围

常用的方法：x=（x-avg）/（max-min）。

如果不这样做的话，会导致递归下降缓慢。。

4. 机器学习模型评估

通过上面的方法，此时我们已经得到了，我们求得的最小损失函数的参数。。

那么我们怎么确保我们的算法是正确的呢，怎么确保我们的递归下降算法是正确的呢。。

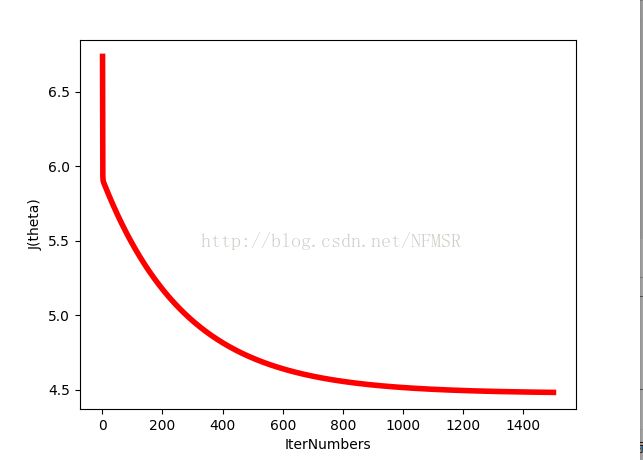
这里我们采用画出损失函数和迭代次数关系的图像，看学习曲线，是否呈现下降的趋势。。。

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------

理论部分结束

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------

开始实战：

这是一个预测店铺受欢迎程度和利润之间的线性回归题，是Coursea上吴恩达老师课程上的练习，上面是要求用Matlab来实现，这里我采用Python语言来实现的。

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

def get_data(file_name):
 data = pd.read_csv(file_name)
 x = []
 y = []
 for popurity ,profit in zip(data["popurity"],data["profit"]):
       x.append([float(popurity)])
       y.append(float(profit))
 return x,y


def getCostFunction(x, y,theat):
     m=len(y)
     h = x.dot(theat)
     cost=1.0/(2*m)*np.sum((h-y)**2)
     return cost

def GradientDescent(x,y,theat):
    m=len(y)
    alpha=0.01
    iterNumbers=1500
    J_history=np.zeros((iterNumbers,1))
    for i in range(iterNumbers):
        h = x.dot(theat)
        #注意这里必须是1.0/m,因为如果是1/m则结果肯定为0
        p=theat[0]-alpha*(1.0/m)*(np.sum((h-y)*(x[:,0]).reshape(97,1),0))

        q = theat[1] - alpha*(1.0/m) * (np.sum((h-y) * (x[:,1]).reshape(97,1),0))
        theat[0]=p
        theat[1]=q

        J_history[i]=getCostFunction(x,y,theat)
        i = i + 1
    return theat,J_history


def predict(x,theat):
    y=x.dot(theat)
    return y

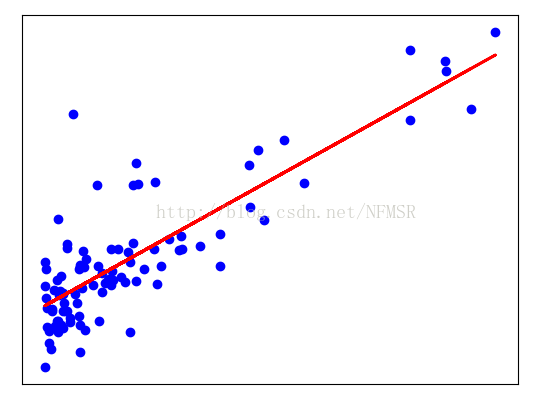
popurity, profit=get_data("../ex1data1.txt")
plt.scatter(popurity, profit, color='blue')
plt.xticks(())
plt.yticks(())
#将数据转换成矩阵

matix=np.array(popurity)
x0=np.ones((len(matix),1))
x=np.hstack((x0,matix))

y=np.array(profit).reshape((97,1))

theat=np.zeros((2,1))

theat,history=GradientDescent(x,y,theat)

plt.plot(popurity,predict(x,theat),color='red',linewidth=2)

plt.figure('visualJFUnction')
plt.xlabel('IterNumbers')
plt.ylabel('J(theta)')
plt.plot((np.arange(1500)+1).reshape(1500,1), history, color='red', linewidth=4)
plt.show()