Java算法学习：使用回溯求一个数组的全排列（递归求解）

全排列，简单的来说就是n个数字中，列出n！（n的阶乘）个排列组合，比如：123的全排列有123、132、213、231、312、321

这种概念在修完高中要求的概率论之后，就应该会有。

那么使用Java语言实现这种全排列，比如求一个数组1，2，3的全排列，这种应该如何实现呢，这几天在学习dfs的时候，遇到了一类题型，利用的就是全排列的思想，把所有可能的结果都列出来。

下面我来讨论一个全排列的递归解决办法：

题目：

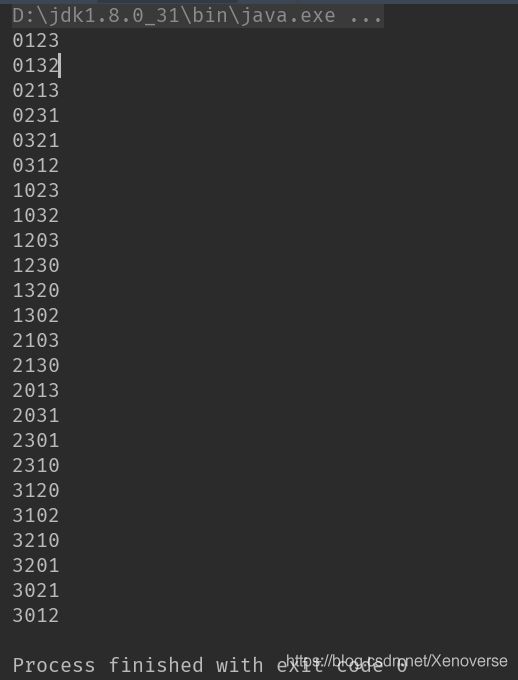
求一个数组的全排列，给定数组｛0,1,2,3｝

样例输入输出：

使用DFS+回溯的方式解决。

解决方案：

针对这种全排列的问题，一般都是用多路递归的方式，不同于之前接触的单路分支，多路分支一般都使用一个for循环创建多路，在这里，就是先将0，1，2，3每个数字都遍历到，每个取出来轮流当第一个元素，每一个分支都负责把剩下的三个元素进行再次的全排列。

比如第一个取出的数字一定是0，那么剩下的数字就是1，2，3。这里就创建了第二个分支，在这个分支里面，我们第一个取出的一定是1，当我们取出1之后，我们还剩下两个数字，2，3，这里我们又创建了第三个分支，在第三个分支里面，我们第一个取出的就是2，2之后我们就只剩下一个元素3了，当我们到了第四个分支，也就是只有一个节点的分支的时候，我们创建的分支数目和全排列出的结果的长度一致，都是4。那么我们就进行第一次输出。

接下来，我们要做的就是回到上一个分支，看看3这个节点有没有兄弟节点，若没有，跳回上一层节点，看看2这个节点有没有兄弟节点。

这个搜索的路线和深度优先搜索的先序遍历完全一致，也就是先搜索左边子树，再搜索右边子树，一条路走到“黑”（意思就是到了树叶节点之后就返回上一层节点探查令一个分支）。

当然，这里想要实现各种排列输出，我们就需要一个基本动作就是交换元素之间的顺序，比如0132，对于数组0123我们就需要把[2]和[3]这两个下标的元素进行一个交换。交换的意思就是，在这个分支里面，我想要让下标为[3]的元素当一次首元素，然后对这个元素进行分支。最后进行输出。输出完事儿之后跳回上一个分支，如果这个分支有兄弟节点，就进入，否则，再跳回上一个分支。下面就是第一个分支进入0开头的排列的情况：

我们可以看到，这里的思想就是，每一层节点，都是一个把集合里每个元素都取出来当作首元素，然后剩余元素在下一层进行选取或者输出。

代码实现：

这里使用java语言实现这一算法。

首先是一个数组，里面存放待排的数字：

public static char[] chars = {'0','1','2','3'};

ok，接下去我们应该有相应函数的入口。我们暂定处理函数的名字叫dfs，从main函数中，应该先从第0个元素开始操作，那我们的main函数应该如下书写。

 public static void main(String[] args) {
        dfs(chars,0);
    }

上面解决方案中既然说到，一定是多路递归，使用一个for循环，并且在for循环里面实现递归。那么我们dfs函数的基本框架一定是。

    public static void dfs(char[] chars,int k){
        if(跳出递归条件){ 
            //做一些操作
        }
        for(int i =k;i

上面就是这个题目最核心的代码框架，for循环创造的是多路递归，在dfs调用的下方就是典型的回溯，将上一次的交换重新恢复原样。这样任何一个分支都是共享一个初始状态的数组。这样每个元素都会被提到前面作为第一个元素。

我们继续补充代码，发现这个递归跳出的条件就是深度搜索到第4个元素[index==3]的时候，所以我们dfs（chars，k+1），当k+1为4的时候，我需要跳出和输出，因为这个时候已经搜索到最后一个元素了，已经完成了一组排列，我们输出即可。

这时候，我们的代码就是这样。

    public static void dfs(char[] chars,int k){
        if(k==chars.length){
            String s= new String(chars);
            if(check(s)){
                System.out.println(s);
            }
        }
        for(int i =k;i

checks函数其实在本题没有什么用。如果是在别的题目中可能要起到一个格式的判断。这里的checks永远return的是true。

完整代码：

完整代码如下。

public class _全排列{

    public static char[] chars = {'0','1','2','3'};

    public static boolean check(String s){
        return true;
    }

    public static void dfs(char[] chars,int k){
        if(k==chars.length){
            String s= new String(chars);
            if(check(s)){
                System.out.println(s);
            }
        }
        for(int i =k;i

总结和反思：

在学习这题的时候有两个注意点：

1. 记住这个全排列的模版，因为在很多地方都需要搜索每个发生的情况。所以dfs是个很好的解决方法。
2. 如果不能理解别人文字描述的思路，一定要使用debug并且画图（树）、记录参数的方法来理解递归过程