天池开发者1024编程battle赛-精神小伙场
本次是阿里云天池平台上的在线编程battle赛,详细信息如下
比赛地址:
【精神小伙场】水一波礼品队
【精神小伙场】次次AC队
活动规则:
1、参赛者将与对手【次次AC队】进行较量,答出一题即可上榜,上榜人数多的一方取得胜利并瓜分【精神小伙场】所含34万积分 (可在天池兑换各种丰厚奖品)。 2、请在10月24日下午20:00-22:00期间答题,比赛结束后可以答题但不计入排行榜。 3、排行榜采用ACM赛制,总用时为罚时+答题时间总和。排行榜每2分钟更新1次,22点显示排行榜最终结果。 4、代码中请勿包含任何个人信息、账号、口令等信息,以免造成泄漏。 5、比赛答疑和交流欢迎加入钉钉群:35215271 6、积分会在5个工作日内自动发放至个人账号
奖品设置:
获胜一方上榜选手均分34万积分(天池粮票) 粮票兑换奖品链接:https://tianchi.aliyun.com/home/souvenir
参赛题目:
| 题目 | 难度 | 通过率 | 状态 |
|---|---|---|---|
| 1.笛卡尔积 | 中等 | 91% | |
| 2.解码方式 | 困难 | 67% | |
| 3.数字消除 | 简单 | 28% | |
| 4.连接两个字符串中的不同字符 | 简单 | 71% |
我是作为“水一波礼品队”参加的,下面是本次比赛的做题过程及题解分析,仅此记录学习一下
连接两个字符串中的不同字符
题目描述:
给出两个字符串, 你需要修改第一个字符串,将所有与第二个字符串中相同的字符删除, 并且第二个字符串中不同的字符与第一个字符串的不同字符连接
示例:
样例 1:
输入 : s1 = "aacdb", s2 = "gafd"
输出 : "cbgf"
样例 2:
输入 : "abcs", s2 = "cxzca"
输出 : "bsxz"
思路:先遍历s1中的字符判断是否在s2中,如果不在就添加到最后结果中;然后同理再遍历s2
代码:
class Solution {
public:
/**
* @param s1: the 1st string
* @param s2: the 2nd string
* @return: uncommon characters of given strings
*/
string concatenetedString(string &s1, string &s2) {
// write your code here
int i;
//存储最后结果
string result="";
//遍历查找s1中的不在s2中的字符
for(i=0;i数字消除
题目描述:
给定一个数字构成的字符串,如果连着两个数字都相同,则可以消除,消除后前部分和后部分会连在一起,可以继续进行消除,现在问你能消除几次?
1 ≤ l e n ( s ) ≤ 1000000 1 \leq len(s) \leq 1000000 1≤len(s)≤1000000
示例:
Example 1:
Input: "43211234"
Output: 4
Example 2:
Input: "101"
Output: 0
思路:遍历字符串,判断当前字符与下一位置字符是否相同,相同则使用earse函数删除相同的这两个字符,然后回退到上一个字符进行判断。注意特殊情况前两个字符相同时不进行回退。
代码:
class Solution {
public:
/**
* @param Numbers: a string of Numbers
* @return: returns the number of eliminations
*/
int NumberOfErasures(string &Numbers) {
// write your code here.
//记录消除次数
int result=0;
for(int i=0;i笛卡尔积
题目描述:
我们采用二维数组setList[][]表示集合数组,其中setList[i]中的每个元素都为整数,且不相同。求集合setList[0],setList[1],…,setList[setList.length - 1]的笛卡尔积。 一般地,集合A和集合B的笛卡尔积A×B = {(x,y)|x∈A∧y∈B}。
1 <= setList.length <= 51 <= setList[i].length <= 5
示例:
样例1
输入:
setList = [[1,2,3],[4],[5,6]]
输出: [[1,4,5],[1,4,6],[2,4,5],[2,4,6],[3,4,5],[3,4,6]]
解释:
[1,2,3]和[4]和[5,6]的笛卡尔积为[[1,4,5],[1,4,6],[2,4,5],[2,4,6],[3,4,5],[3,4,6]]
样例2
输入:
setList = [[1,2,3],[4]]
输出: [[1,4],[2,4],[3,4]]
解释:
[1,2,3]和[4]的笛卡尔积为[[1,4],[2,4],[3,4]]
思路:
这道题自己没做出来,本来是想遍历setList中的每个向量元素,有多少个向量元素就写多少个for循环,但是向量元素的个数不确定没办法写for循环不知道写几个,不过setListl.length<=5,可以穷举出来所有的可能可以用很多个for循环穷举(个数为2时2个for循环为3时3个for循环…也可以写5个for循环循环前添加判断条件,循环中用push_back(),pop_back(),这种循环其实就是回溯法),网上参考了别的资料,这道题是要用回溯求解,代码如下:
回溯代码:
class Solution {
public:
/**
* @param setList: The input set list
* @return: the cartesian product of the set list
*/
//存储最后结果
vector> ans;
//存储最后结果中的一个元素
vector lv;
vector> getSet(vector> &setList) {
//Write your code here
dfs(setList,0);
return ans;
}
//DFS(深度优先搜索),回溯法
void dfs(vector> &setList,int i){
if(i==setList.size()){
ans.push_back(lv);
return;
}
for(int j=0;j 解码方式
题目描述:
使用以下映射方式将 A-Z 的消息编码为数字:
'A' -> 1
'B' -> 2
...
'Z' -> 26
除此之外, 编码的字符串也可以包含字符 *, 它代表了 1 到 9 的数字中的其中一个.给出包含数字和字符 * 的编码消息, 返回所有解码方式的数量. 因为结果可能很大, 所以结果需要对 10^9 + 7 取模
- 输入的字符串在范围 [1, 10^5] 内.
- 输入的字符串只能包含字符
*和数字0-9.
示例:
样例1
输入: "*"
输出: 9
说明: 你可以译码为 "A", "B", "C", "D", "E", "F", "G", "H", "I".
样例2
输入: "1*"
输出: 18
思路:
这道题比赛时根本没时间看,后来看完一顿乱写,越写越迷,真的还是要有思路,不能是乱碰乱撞式写法,这道题比较复杂,是LeetCode上面的原题解码方法2,还有一道相似的更基础版的题解码方法
我现在太菜了,题解也看得似懂非懂,这道题确实也挺难的,就先把官方题解放在下面
方法一:记忆性递归
算法
对输入的字符序列,考虑每种可能的解码情况。
假设有函数 ways(s,i),返回字符串 ss 中前 ii 个字符的解码方法数量。调用 ways(s, s.length()-1) 得到字符串中所有字符的解码方法数量。
我们从字符串 ss 的最后一个字符开始解码,假设此时调用函数 ways(s,i)。在 ways(s,i) 中计算前 i 个字符的所有解码方法数量。第 i 个字符有以下几种情况。
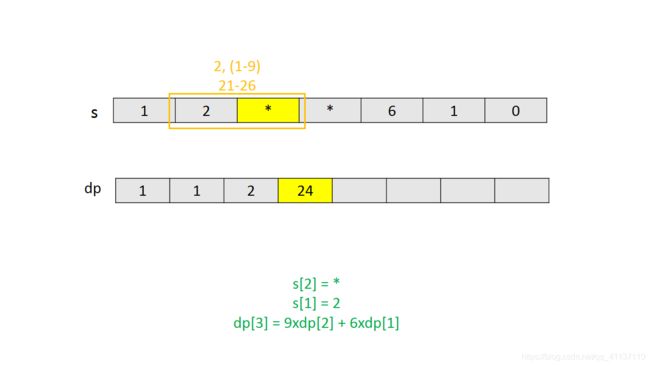
第 i 个字符是 *。首先考虑第$ i$ 个字符单独解码的情况,* 表示 1-9 中任意一个数字,对应 A-I 中任意一个字母。前 i 个字符的解码可以表示为在前 i − 1 i−1 i−1 个字符解码的结尾加上 A-I 中任意一个字母。因此总的解码数量为前$ n-1$个字符解码数量的 9 倍,即 9*ways(s,i-1)。
除此之外,第 $ i$ 个字符也可以和第 i − 1 i−1 i−1 个字符一起解码。如果第$ i-1$ 个字符是 1,它们可以表示 11-19 中任意一个数字,对应 K-S 中任意一个字母。前 $ i$ 个字符的解码可以表示为在前 i − 2 i−2 i−2 个字符解码的结尾加上 K-S 中任意一个字母。因此总的解码数量为前 n − 2 n−2 n−2 个字符解码数量的 9 倍,即 9*ways(s,i-2)。需要注意的是使用两个字符 1* 一起解码和两个字符分开单独解码的结果不重复。
如果第 i − 1 i−1 i−1 个字符是 2,那么 2* 可以表示 21-26 中任意一个数字,对应 U-Z 中任意一个字母。总的解码数量是前 i − 2 i−2 i−2 个字符解码数量的 6 倍,即 6*ways(s,i-2)。
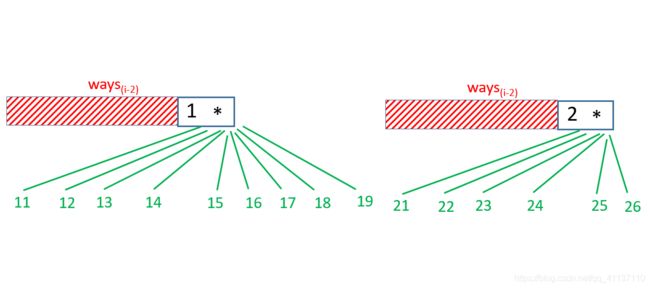
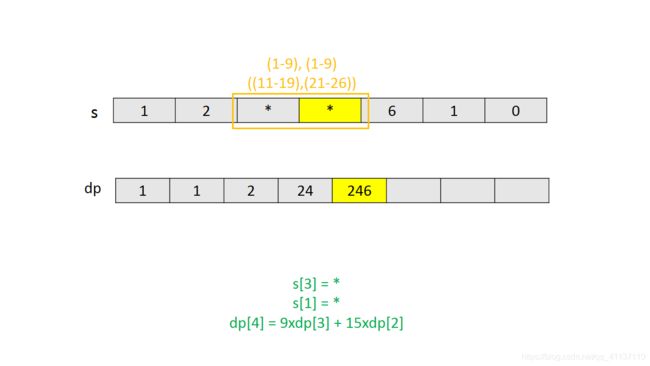
如果第 i − 1 i−1 i−1 个字符是 *,那么** 可以表示 11-19(9)和 21-26(6) 中任意一个数字。因此总的解码数量是前 i − 2 i−2 i−2 个字符解码数量的 15(9+6) 倍,即 15*ways(s,i-2)。
如果第 i i i 个字符是 1-9 的数字。首先考虑单个字符解码的情况。此时前 i i i 个字符的解码数量等于前 i − 1 i-1 i−1 个字符的解码数量。如果第 i i i 个字符是 0,那么它不能单独解码,必须与它的前一个字符一起解码。前一个字符是 1,2 或 * 时才可以解码。具体情况如下。
如果前一个字符是 1,那么它们可以是 10-19 中任意一个数字。此时解码数量等于前 i − 2 i-2 i−2 个字符的解码数量。
如果前一个字符是 2,则有效数字范围为 20-26。只有当前字符小于 7 时可以解码。此时解码数量等于前 i − 2 i−2 i−2 个字符的解码数量。
如果前一个字符是 *,那么解码数量取决于当前数字。如果当前数字大于 6,那么它们只能是 17-19 中任意一个(27-29 是无效的解码数字)。此时解码数量等于前 i − 2 i−2 i−2 个字符的解码数量。
如果当前数字小于 7,则 * 可以是 1 或 2。对应 10-16 或者 20-26 中任意一个数字。此时解码数量等于前 i − 2 i−2 i−2 个字符解码数量的 2 倍。
在函数 ways 中实现所有的情况,递归调用 ways 计算所有字符的解码数量。记录已经计算出来的前 i i i 个字符的解码数量,减少重复调用,降低计算复杂度。
Java代码:
public class Solution {
int M = 1000000007;
public int numDecodings(String s) {
Integer[] memo=new Integer[s.length()];
return ways(s, s.length() - 1,memo);
}
public int ways(String s, int i,Integer[] memo) {
if (i < 0)
return 1;
if(memo[i]!=null)
return memo[i];
if (s.charAt(i) == '*') {
long res = 9 * ways(s, i - 1,memo);
if (i > 0 && s.charAt(i - 1) == '1')
res = (res + 9 * ways(s, i - 2,memo)) % M;
else if (i > 0 && s.charAt(i - 1) == '2')
res = (res + 6 * ways(s, i - 2,memo)) % M;
else if (i > 0 && s.charAt(i - 1) == '*')
res = (res + 15 * ways(s, i - 2,memo)) % M;
memo[i]=(int)res;
return memo[i];
}
long res = s.charAt(i) != '0' ? ways(s, i - 1,memo) : 0;
if (i > 0 && s.charAt(i - 1) == '1')
res = (res + ways(s, i - 2,memo)) % M;
else if (i > 0 && s.charAt(i - 1) == '2' && s.charAt(i) <= '6')
res = (res + ways(s, i - 2,memo)) % M;
else if (i > 0 && s.charAt(i - 1) == '*')
res = (res + (s.charAt(i)<='6'?2:1) * ways(s, i - 2,memo)) % M;
memo[i]= (int)res;
return memo[i];
}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 表示输入字符串和备忘录数组的长度,备忘录数组中每项计算时间复杂度为 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( n ) O(n) O(n),递归树的深度为 n n n。
方法二:动态规划
算法
从 方法一 可以看出,字符串前 i i i 个字符的解码方法数量只与前 i i i 个字符有关,与它后面的字符无关。因此该问题也可以使用动态规划解决。
如果知道字符串前 i − 1 i−1 i−1 个字符的解码数量和前 i − 2 i−2 i−2 个字符的解码数量,就可以计算出前 i i i 个字符的解码数量。从前往后计算数组 d p dp dp 中每一项, d p [ i ] dp[i] dp[i] 表示字符串 s s s 前 i i i 个字符的编码数量。
通过一个简单实例的图解说明 d p dp dp 的计算过程。

Java代码
public class Solution {
int M = 1000000007;
public int numDecodings(String s) {
long[] dp = new long[s.length() + 1];
dp[0] = 1;
dp[1] = s.charAt(0) == '*' ? 9 : s.charAt(0) == '0' ? 0 : 1;
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == '*') {
dp[i + 1] = 9 * dp[i];
if (s.charAt(i - 1) == '1')
dp[i + 1] = (dp[i + 1] + 9 * dp[i - 1]) % M;
else if (s.charAt(i - 1) == '2')
dp[i + 1] = (dp[i + 1] + 6 * dp[i - 1]) % M;
else if (s.charAt(i - 1) == '*')
dp[i + 1] = (dp[i + 1] + 15 * dp[i - 1]) % M;
} else {
dp[i + 1] = s.charAt(i) != '0' ? dp[i] : 0;
if (s.charAt(i - 1) == '1')
dp[i + 1] = (dp[i + 1] + dp[i - 1]) % M;
else if (s.charAt(i - 1) == '2' && s.charAt(i) <= '6')
dp[i + 1] = (dp[i + 1] + dp[i - 1]) % M;
else if (s.charAt(i - 1) == '*')
dp[i + 1] = (dp[i + 1] + (s.charAt(i) <= '6' ? 2 : 1) * dp[i - 1]) % M;
}
}
return (int) dp[s.length()];
}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是输入字符串的长度,数组 d p dp dp 长度为 n + 1 n+1 n+1,计算数组每一项的时间复杂度为 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( n ) O(n) O(n),数组 d p dp dp 的长度为 n + 1 n+1 n+1。
方法三:恒定空间的动态规划
算法
只要知道 d p [ i − 2 ] dp[i-2] dp[i−2] 和 d p [ i − 1 ] dp[i-1] dp[i−1] 就可以计算出 d p [ i ] dp[i] dp[i]。因此不需要保存数组 d p dp dp 的所有值,只需要记录数组 d p dp dp 的最后两个值就可以计算出下一项。其他过程与 方法二 相同。
Java代码
public class Solution {
int M = 1000000007;
public int numDecodings(String s) {
long first = 1, second = s.charAt(0) == '*' ? 9 : s.charAt(0) == '0' ? 0 : 1;
for (int i = 1; i < s.length(); i++) {
long temp = second;
if (s.charAt(i) == '*') {
second = 9 * second;
if (s.charAt(i - 1) == '1')
second = (second + 9 * first) % M;
else if (s.charAt(i - 1) == '2')
second = (second + 6 * first) % M;
else if (s.charAt(i - 1) == '*')
second = (second + 15 * first) % M;
} else {
second = s.charAt(i) != '0' ? second : 0;
if (s.charAt(i - 1) == '1')
second = (second + first) % M;
else if (s.charAt(i - 1) == '2' && s.charAt(i) <= '6')
second = (second + first) % M;
else if (s.charAt(i - 1) == '*')
second = (second + (s.charAt(i) <= '6' ? 2 : 1) * first) % M;
}
first = temp;
}
return (int) second;
}
}
复杂度分析
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 是输入字符串的长度,需要计算到第 n n n 次才能得到所有字符的解码数量。
- 空间复杂度: O ( 1 ) O(1) O(1),使用恒定空间。
知识点
递归、回溯和DFS的区别
- 递归是一种算法结构,回溯是一种算法思想。
- 一个递归就是在函数中调用函数本身来解决问题。
- 回溯就是通过不同的尝试来生成问题的解,有点类似于穷举,但是和穷举不同的是回溯会“剪枝”
回溯搜索是深度优先搜索(DFS)的一种。对于某一个搜索树来说(搜索树是起记录路径和状态判断的作用),回溯和DFS主要的区别是,回溯法在求解过程中不保留完整的树形结构,而深度优先搜索则记下完整的搜索树。
递归的一般结构
void f()
{
if(符合边界条件)
{
///
return;
}
//某种形式的调用
f();
}
回溯的一般结构
void DFS(int 当前状态)
{
if(当前状态为边界状态)
{
记录或输出
return;
}
for(i=0;i总结
数字消除这道题做的时候感觉还挺简单的,不知道为什么这道题的通过率反而是最低的,通过率28%提交次数243。解码方式这道最难的题反而通过率高达67%,提交次数91,不知道都怎么做的,有没有百度,我觉得还是自己好好做吧,主要为了提高自己嘛,成绩不那么重要。这次比赛在线编辑运行测试数据、提交代码检测结果太慢了,我提交完数字消除这道题后太慢了我才做的笛卡尔积那道题,数字消除还挺有自信的感觉是对的,好久才出评判结果,评判出错后我想着应该好改,就在做笛卡尔积那道题没怎么着急改,所以最后没有及时提交那道题。前三题都还可以,最后一道题感觉有点晕,也是我现在做题少的原因还是太菜了,继续加油吧。