【吴恩达机器学习】线性回归 Linear Regression

线性回归(Linear Regression)

单变量线性回归 (Linear regression with one variable / Univariate linear regression)
多变量线性回归 (Linear regression with multiple variables / Multivariate linear regression)

---

标记符号:

• $m$ — 训练样本的数量
• $x$ — 输入变量/特征
• $y$ — 输出变量
• $(x,y)$ — 一个训练样本
• $(x^{(i)},y^{(i)})$ — 第$i$个训练样本
• $n$ — 特征的数量
• $x^{(i)}$ — 第$i$个样本输入
• $x_j^{(i)}$ — 第$i$个样本输入的第$j$个特征

---

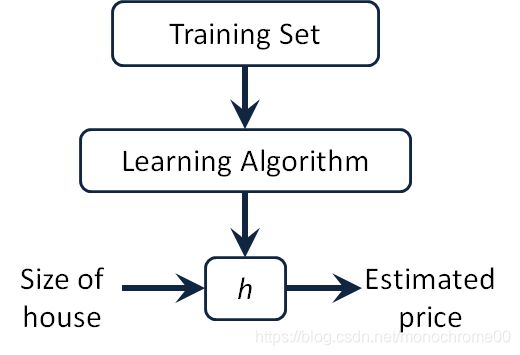
假设函数（Hypothesis）

假设函数表示对于某一个输入样本$x$，返回对应预测的值$h$，而真实值是$y$。
假设函数基于参数$\theta$，其表达式如下：
$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$$

另外的定义 $x_0=1$，那么假设函数就可以通过两个向量的乘积来表示：
$$x=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ .\\ .\\ .\\ x_n\end{array}\right]\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\\ .\\ .\\ .\\ {\theta }_n\end{array}\right]$$

$$\begin{array}{rl}{h}_{\theta }(x)& ={\theta }_0{x}_0+{\theta }_1{x}_1+...{\theta }_n{x}_n\\ & ={\theta }^{T}x\end{array}$$

---

代价函数（Cost Function）

代价函数用于评判模型的好坏，类似于假设函数所得值与实际值的方差：
$$J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

---

梯度下降（Gradient Descent ）

“Batch” Gradient Descent
“Batch”: Each step of gradient descent uses all the training examples.

$n$个特征的梯度下降一般算法：
$$\begin{array}{rl}& repeatuntilconvergence\{\\ & {\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1...{\theta }_n)\\ & \}\end{array}$$

化简一下就可得：
$$\begin{array}{rl}& repeatuntilconvergence\{\\ & {\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\ast x_j^{(i)}\\ & \}\end{array}$$

用后面所说的设计矩阵表示的话会更加简单：
$$\begin{array}{rl}& repeatuntilconvergence\{\\ & \theta :=\theta -\alpha \frac{1}{m}(X{\theta }^T-y{)}^{T}X\\ & \}\end{array}$$

• $\alpha$ (Learning rate): 控制参数$\theta$变化的快慢

  • 如果 $\alpha$ 太小，梯度下降就会太慢
  • 如果 $\alpha$ 太大，在跌倒中，有可能越过最低点，代价函数 $J(\theta )$ 可能会上升; 最后不能收敛(converge)，甚至发散(diverge)。
  • 对于$\alpha$, 可以这样一次乘三倍的去尝试 $...,0.001,0.003,0.01,0.03,0.1,0.3,1,...$

• 梯度(Gradient) 也就是下降速度，表示为斜率，每个参数按照不同方向的斜率，尽快的下降。越接近最小值，变化速率也会随着斜率的减小自动的减小。

• 梯度下降很容易陷入局部最优，只要初始值偏离一点，最后也可能会落在不同的最优处。

• 但是对于线性回归来说，所有的函数都是凸函数，也就是说局部最优就是全局最优。

---

特征缩放（Feature Scaling）

• 在多元线性回归中，两个变量范围相差太大，每一次迭代的步子都可能会非常小，也就需要很多的迭代次数。

• 特征缩放的目的是让所有的变量$x_i$取值都在 $-1\le x_i\le 1$ 之间。吴恩达给出的上下限：$(-3,3),(-\frac{1}{3},\frac{1}{3})$

• 均值归一（Mean normalization）： $x_i=\frac{x_i-{\mu }_i}{s_i}$

  ​ ${\mu }_i=x_i\text{的平均值}$

  ​ $s_i=x_i\text{的取值范围}(max-min)$

---

多项式回归（Polynomial regression）

• 对于多项式模型的假设函数，如：$h_{\theta }={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3$，可以令$x_1=x,x_2=x^2,x3=x^3$，然后使用普通线性回归的梯度下降即可。
• 通常需要特征缩放。

---

正规方程（Normal Equation）

对于 $m$ 个样本，$n$ 个特征 的训练，我们可以表示$m$个输入$x^{(i)}$和一个输出$y$
把所有的特征向量$x^{(i)}$构造出设计矩阵(design matrix)$X$。
$$x^{(i)}=\left[\begin{array}{c}{x}_0^i\\ x_1^i\\ x_2^i\\ .\\ .\\ .\\ x_n^i\end{array}\right]\in {\mathbb{R}}^{n+1}X=\left[\begin{array}{c}(x^{(1)}{)}^T\\ (x^{(2)}{)}^T\\ .\\ .\\ .\\ (x^{(m)}{)}^T\end{array}\right]y=\left[\begin{array}{c}{y}^{(1)}\\ y^{(2)}\\ .\\ .\\ .\\ y^{(m)}\end{array}\right]$$
那么就可以神奇的得到向量$\theta$，里面的数就是最优的参数。
$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$

与梯度下降相比，正则化不需要计算出$\alpha$，也不需要多次的迭代。但如果$n$太大，它的效率也不高，因为$X^{T}X$是一个$n\times n$的矩阵，求逆的复杂度是$O(n^3)$

• 一般情况下$X^{T}X$都是可以求逆的，就算不可以求逆，$Octave$里的函数$pinv$也能够计算出逆。
• 不可求逆的一般原因：
  • 特征之间线性依赖，存在多余的特征
  • 特征过多 ($m\le n$)
    • 删除掉无关特征，或者使用正则化(regularization)

---

参考资料

[1].吴恩达机器学习 第二章-单变量线性回归
[2].吴恩达机器学习 第五章-多变量线性回归
[3].黄海广博士笔记