基于C++的带权无向图的实现 (一)- 数据结构
该系列文章是本人整理的有关带权无向图的数据结构和算法的分析与实现,如有问题或者建议欢迎各位指出。
目录
基于C++的带权无向图的实现 (一)- 数据结构
基于C++的带权无向图的实现 (二)- 遍历算法
基于C++的带权无向图的实现 (三)- Prim最小生成树算法
基于C++的带权无向图的实现 (四)- Dijkstra最短路径算法
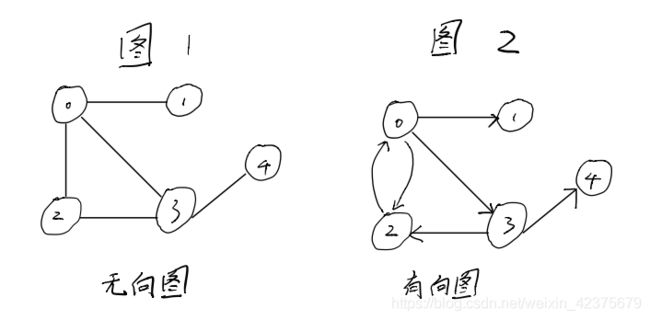
图的基本概念
-
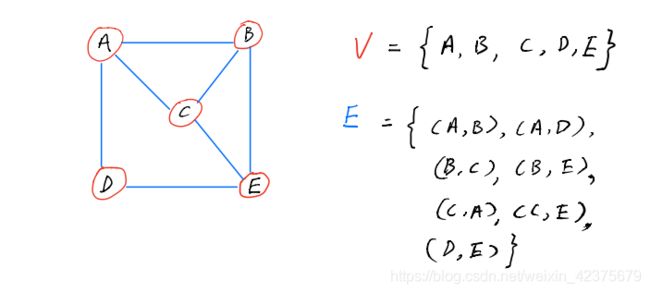
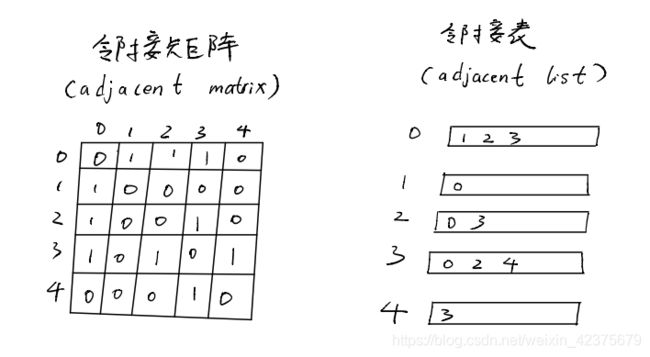
邻接矩阵中,横轴和纵轴表示的数字分别为顶点,矩阵中的“0”和“1”表示两个顶点间是否有相邻关系。邻接矩阵中主对角线都是0因为顶点不可能与本身具有相邻关系。要知道某个顶点的度数,只需要求该顶点所在的行或者列的和即可。
-
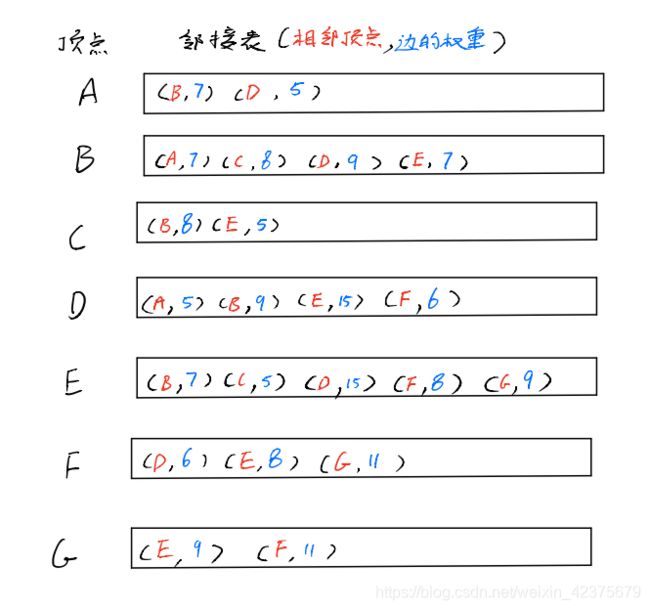
邻接表是一种数组与链表(或集合)结合的存储方法,其中数组用来存放所有顶点,链表(或集合)用来存在该顶点的所有邻接顶点。
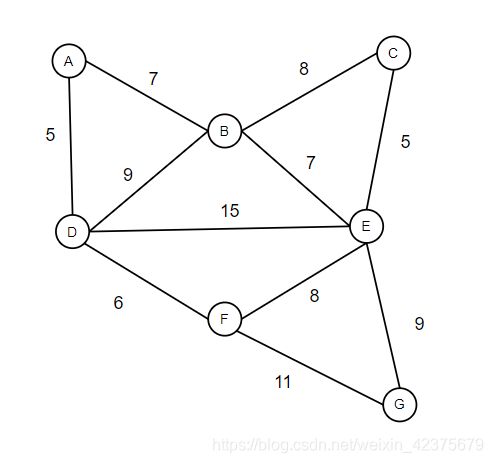
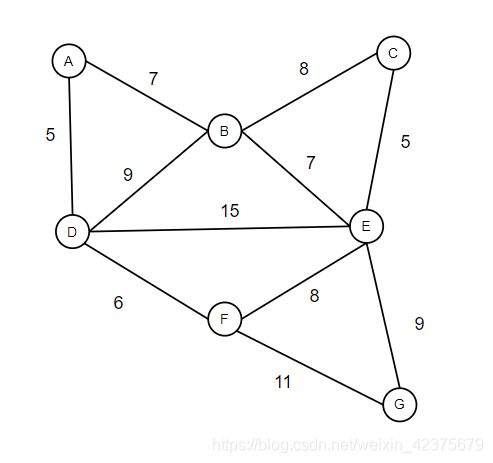
- 如果顶点之间的边加上权重,则可以表示如下:
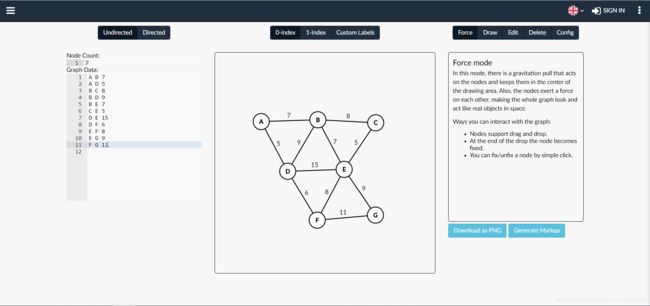
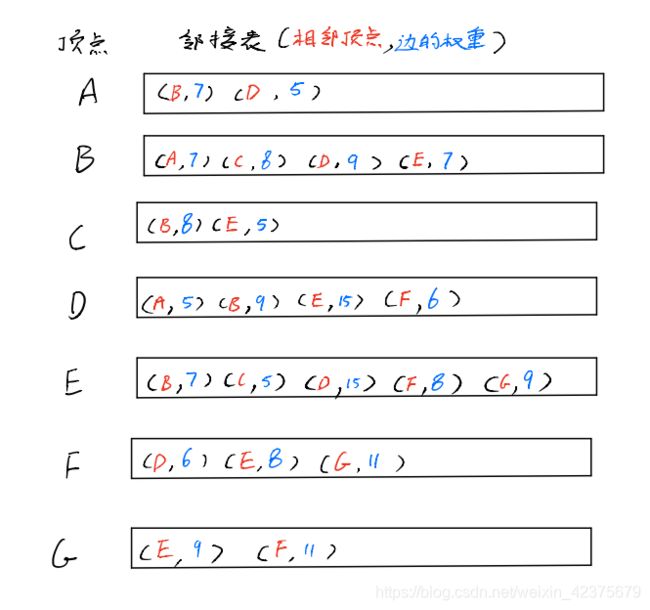
本文所实现的就是这种带权重的无向图,测试案例用的就是该图顶点和边的数据,最终存储在如下所示的邻接表中:
定义类
图类(class Graph)
由于C++中存在很多高效的STL容器,这里使用了map和set两种关联式容器来存储顶点和边的数据。
-
map:存储键值对(key-value)的容器,提供一对一(其中第一个可以称为关键字,每个关键字只能在map中出现一次,第二个可以称为该关键字所对应的值)的数据处理能力。这里我把顶点设置为键,其对应的邻接点和边的权重的集合设置为值。
-
set:不会有相同元素,并且存进去的元素会自动进行升序排序(默认情况下),set就是每一个顶点的邻接表。
来存储每一个顶点及其邻接点和权重集合,设置了模板"T"后图就可以存储任何数据类型的数据。
template <typename T>
class Graph {
public:
map<T, set<Edge<T>>> adj;
};
边类(class Edge)
类中有两个成员变量,其中vertex表示相邻顶点,weight表示权重。
template <typename T>
class Edge {
public:
T vertex;
int weight;
};
功能描述
在Graph类中实现了以下功能,T为提前定义好的模板:
| 函数名 | 用途 |
|---|---|
| bool contains(const T& u) | 判断图内是否存在顶点u |
| bool adjacent(const T& u, const T& v) | 判断顶点u和v是否相邻 |
| void add_vertex(const T& u) | 在图中添加顶点u |
| void add_edge(const T& u, const T& v, int weight ) | 给顶点u和v添加边 |
| void change_weight(const T& u, const T& v, int weight) | 改变顶点u和v之间边的权重值 |
| void remove_weight(const T& u, const T& v) | 删除顶点u和v之间边的权重值 |
| void remove_vertex(const T& u) | 删除给定的顶点u, 同时清除所有入射边 |
| void remove_edge(const T& u, const T& v) | 删除两个顶点之间的边 |
| int degree(const T& u) | 返回顶点的入射边数 |
| int num_vertices() | 返回图中的顶点总数 |
| int num_edges() | 返回图中的边的总数 |
| int largest_degree() | 返回最大顶点的度数。 |
| int get_weight(const T& u, const T& v) | 返回顶点u和v之间边的权重值 |
| vector get_vertices() | 返回图形中所有顶点ID的vector向量 |
| vector get_neighbours(const T& u) | 返回给定顶点的所有相邻顶点ID的vector向量。 |
void show()| 打印图中所有数据
代码实现
- 在“edge.hpp”中的代码如下:
template <typename T>
class Edge {
public:
T vertex;
int weight;
Edge(T neighbour_vertex) {
this->vertex = neighbour_vertex;
this->weight = 0;
}
Edge(T neighbour_vertex, int weight) {
this->vertex = neighbour_vertex;
this->weight = weight;
}
bool operator<(const Edge& obj) const {
return obj.vertex > vertex;
}
bool operator==(const Edge& obj) const {
return obj.vertex == vertex;
}
};
重载了"<“和”=="运算符,这样Edge的对象就可以在集合中进行排序和查找。
- 在“graph.hpp”中的代码如下:
#include测试
在“graph_testing.cpp”中的代码如下:
#include "graph.hpp"
void test01(Graph<char> g)
{
cout << "'A' 和 'D'之间边的权重为:" << g.get_weight('A', 'D') << endl;
g.change_weight('A', 'D', 100);
cout << "将'A' 和 'D'之间边的权重更改为100后,其权重为:" << g.get_weight('A', 'D') << endl;
g.remove_weight('A', 'D');
cout << "将'A' 和 'D'之间边的权重删除后,其权重为:" << g.get_weight('A', 'D') << endl;
cout << "将'A' 和 'D'之间边的权重重新设置为5" << endl;
g.change_weight('A', 'D', 5);
cout << "顶点总数:" << g.num_vertices() << endl;
cout << "边的总数:" << g.num_edges() << endl;
cout << "图中包含'F'吗?" << (g.contains('F') ? "包含" : "不包含") << endl;
cout << "图中包含'G'吗?" << (g.contains('G') ? "包含" : "不包含") << endl;
cout << "'A'和'D'相邻吗?" << (g.adjacent('A', 'D') ? "相邻" : "不相邻") << endl;
cout << "'B'和'E'相邻吗?" << (g.adjacent('B', 'E') ? "相邻" : "不相邻") << endl;
cout << "顶点'A'的度数为: " << g.degree('A') << endl;
cout << "最大度数为:" << g.largest_degree() << endl;
auto vertices = g.get_vertices();
cout << "图中的顶点分别为:";
for (auto u : vertices) cout << " " << u;
cout << endl;
auto nbrs = g.get_neighbours('F');
cout << "顶点F的邻接结点为:";
for (auto u : nbrs) cout << " " << u;
cout << endl;
}
int main()
{
Graph<char> g;
g.add_vertex('A');
g.add_vertex('B');
g.add_vertex('C');
g.add_vertex('D');
g.add_vertex('E');
g.add_vertex('F');
g.add_vertex('G');
g.add_edge('A', 'B', 7);
g.add_edge('A', 'D', 5);
g.add_edge('B', 'C', 8);
g.add_edge('B', 'D', 9);
g.add_edge('B', 'E', 7);
g.add_edge('C', 'E', 5);
g.add_edge('D', 'E', 15);
g.add_edge('D', 'F', 6);
g.add_edge('E', 'F', 8);
g.add_edge('E', 'G', 9);
g.add_edge('F', 'G', 11);
g.add_vertex('H');
g.add_edge('B', 'H', 9);
g.add_edge('A', 'H', 10);
g.add_edge('D', 'H', 11);
g.add_edge('A', 'H', 12);
g.remove_vertex('H');
cout << "打印图中顶点及其邻接表的详细信息如下" << endl;
g.show();
cout << endl;
test01(g);
return 0;
}
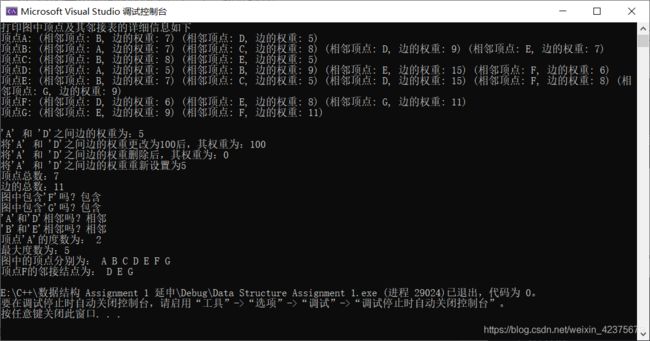
输出结果:
最后,给大家推荐一个可交互的在线绘图的网站Graph Editor,在已知顶点和边的数据后可以在这里左边Node Count栏输入数据进行可视化: