Leetcode-1631 最小体力消耗路径 - 并查集

题目描述

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

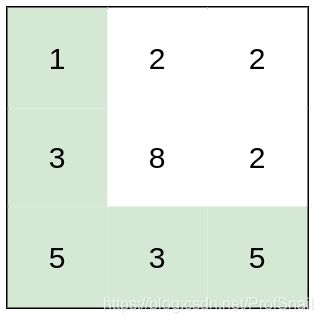
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。
示例 2：

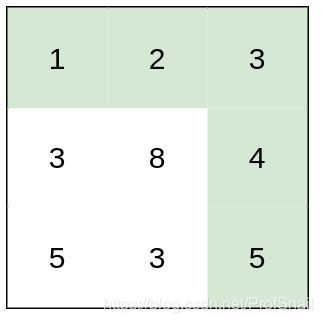
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。
示例 3：

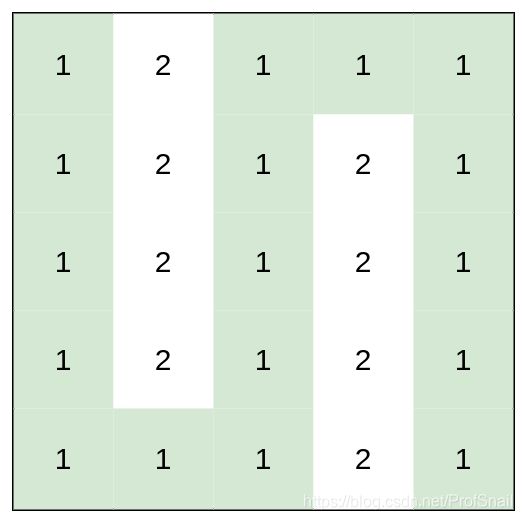
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/path-with-minimum-effort
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

与一般的并查集是用来记录图中连通分量个数不同，这道题使用并查集的思路是逐渐添加边，直到起点和终点处于同一个连通分量（即存在一条路径使得起点和终点相连），插边的过程结束。

• 先把这张图存起来：边为所有上下左右相邻的顶点构成，边权是相邻顶点之间的高度差。
• 策略是什么呢？
• 假设整张图m*n个节点最开始都是孤立点，需要添加一条条的边，使得各个顶点相连，直到起点和终点在同一个集合中，路径就结束了。
• 由于题设中的整个体力消耗值，是路径上所有相邻节点的高度差中的最大值。那么我们一直不停的向整张图中添加权值最小的边，就算添加进来的这条边，在最后的路径中用不到，他也不会让当前图中的路径体力消耗值变得更多。
• 一直添加边，如同上文说到的，直到加上某条边时候，起点和终点处于同一个集合下，那么路径就找到了。又因为咱们是从最小高度差的边一个个添加进来的，所以最后加进来的这条边的权值就是题目要的最小消耗的体力值。返回他就可以了。
• 妙啊~
  

代码

class Union{
     
public:
    int n;
    vector<int> f;
    Union(int _n): n(_n), f(_n){
     
        for(int i = 0; i < _n; i++){
     
            f[i] = i;
        }
    }
    int findf(int x){
     
        int root = x, z;
        while(root!=f[root])root=f[root];
        while(f[x]!=root){
     
            z = f[x];
            f[x] = root;
            x = z;
        }
        return root;
    }
    int merge(int a, int b){
     
        int fa = findf(a);
        int fb = findf(b);
        if(fa!=fb){
     
            f[max(fa, fb)] = min(fa, fb);
        }
        return 0;
    }
};
struct Edge{
     
    int u, v, cost;
    Edge(int _u, int _v, int _cost){
     
        u = _u;
        v = _v;
        cost = _cost;
    }
    bool operator < (const Edge e) const{
     
        return cost < e.cost;
    }
};

class Solution {
     
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
     
        int m = heights.size();
        int n = heights[0].size();
        Union un = Union(m*n);
        vector<Edge> edges;
        for(int i = 0; i < m; i++){
     
            for(int j = 0; j < n; j++){
     
                if(i>0){
     
                    edges.push_back(Edge((i-1)*n+j, i*n+j, abs(heights[i-1][j]-heights[i][j])));
                }
                if(j>0){
     
                    edges.push_back(Edge(i*n+j-1, i*n+j, abs(heights[i][j-1]-heights[i][j])));
                }
            }
        }
        sort(edges.begin(), edges.end());
        int s = 0, e = m*n-1, ans;
        for(auto& edge: edges){
     
            un.merge(edge.u, edge.v);
            if(un.findf(s)==un.findf(e)){
     
                return edge.cost;
            }
        }
        return 0;
    }
};