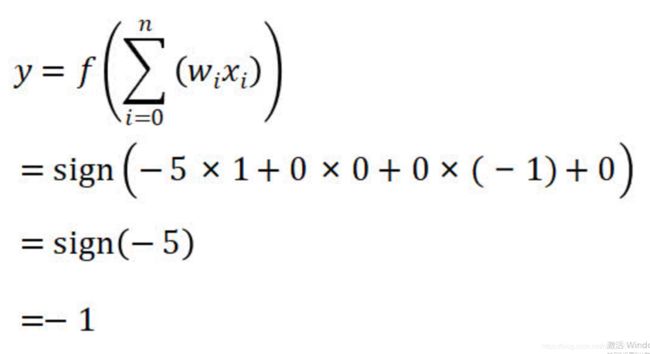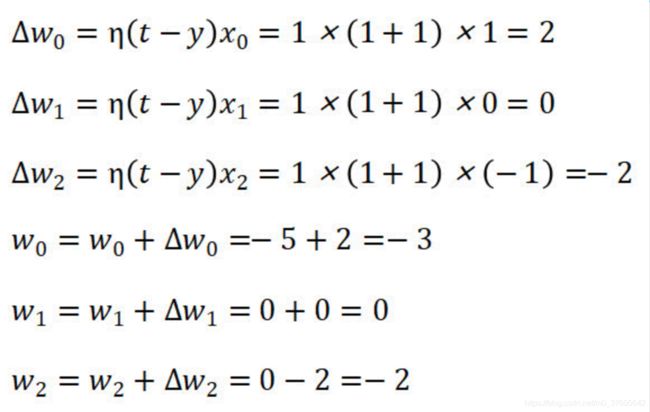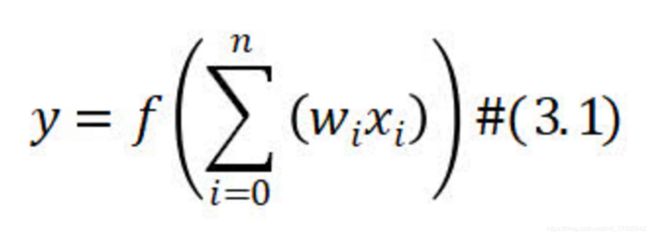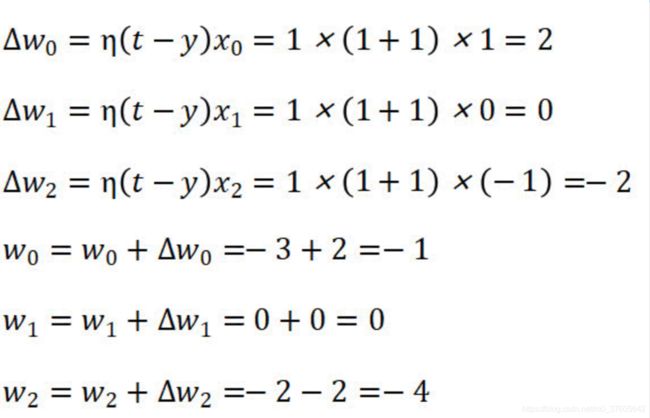【机器学习】简单理解单层感知器
机器学习入门教程：单层感知机
参考文章：
深度学习之(神经网络)单层感知器（python）（一）
超详细！带你走进单层感知器与线性神经网络
一、单层感知机的由来
神经元结构
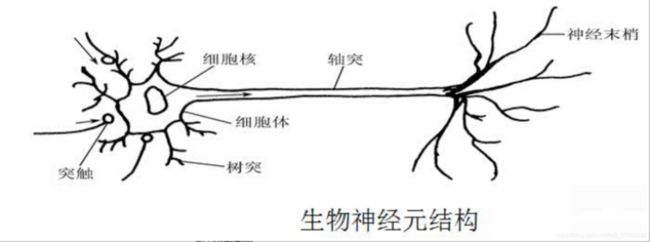
输入神经元（x） ：input
传出神经元（y）：output
刺激强度（w1，w2，w3）
细胞体自身信号（偏置值b）
单层感知机只有输入层、输出层，没有隐藏层；多层感知机，既有输入层，又有输出层，还有隐藏层
单层感知器结构【第一种表达形式】
受到生物神经网络的启发，计算机学家Frank Rosenblatt在20世纪60年代提出了一种模拟生物神经网络的的人工神经网络结构，称为感知器(Perceptron)。
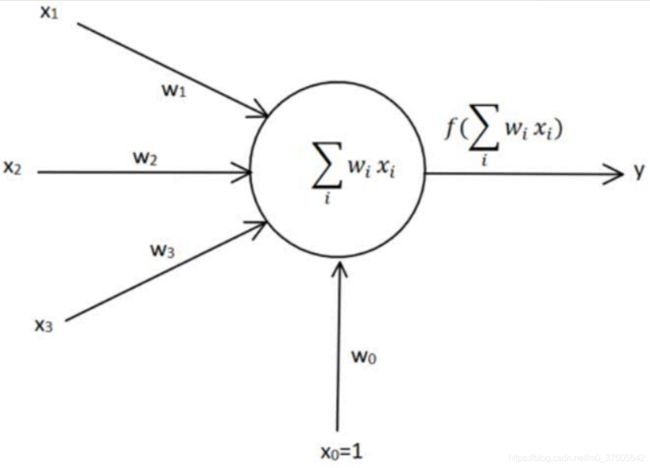
二、单层感知机的原理介绍
单层感知机原理
三、单层感知机计算举例【第一种表达形式】
1. 一个单层感知器有3个输入x1,x2,x3，w1=w2=w3=0.5，偏置b=-0.6
输出y
计算结果
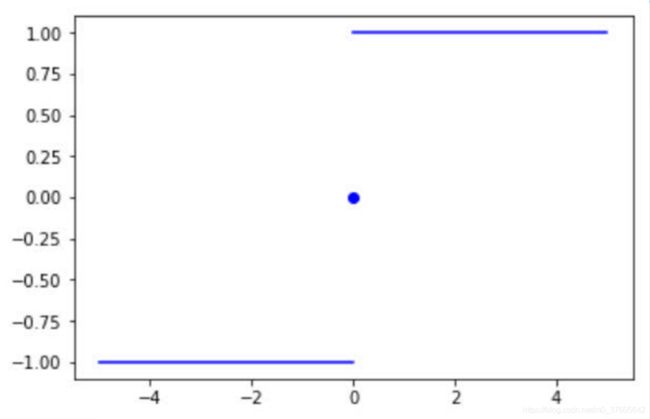
2. 介绍一下，符号函数sign(x)，也是激活函数：
该函数的特点是当x＞0时，输出值为1；当x＝0时，输出值为0,；当x＜0时，输出值为-1
sign(x)图像
三、单层感知机计算举例【第二种表达形式】
单层感知器结构【第二种表达形式】
1. 一个单层感知器有3个输入x0=1，x1=0，x2=-1，w0=-5，w1=0，w2=0，学习率=1，正确的标签t=1
(注意在这个例子中偏置值b用w0×x0来表示，x0的值固定为1)
【step1】
计算y值
由于y=-1与正确的标签t=1不相同，所以需要对感知器中的权值进行调节。
重新调整权值
【step2】
y值计算公式
由于y=-1与正确的标签t=1不相同，所以需要对感知器中的权值进行调节。
重新调整权值
【step3】
同理，重新计算y
重新计算y值
由于y=1与正确的标签t=1相同，说明感知器经过训练后得到了我们想要的结果，结束训练。
四、Python代码实现
# coding: utf-8
# In[ ]:
import numpy as np
import matplotlib.pyplot as plt
# In[ ]:
#输入数据
X = np.array([[1,3,3],
[1,4,3],
[1,1,1]])
#标签
Y = np.array([1,1,-1])
#权值初始化，1行3列，取值范围-1到1
W = (np.random.random(3)-0.5)*2
print(W)
#学习率设置
lr = 0.11
#计算迭代次数
n = 0
#神经网络输出
O = 0
def update():
global X,Y,W,lr,n
n+=1
O = np.sign(np.dot(X,W.T))
W_C = lr*((Y-O.T).dot(X))/int(X.shape[0])
W = W + W_C
# In[ ]:
for _ in range(100):
update()#更新权值
print(W)#打印当前权值
print(n)#打印迭代次数
O = np.sign(np.dot(X,W.T))#计算当前输出
if(O == Y.T).all(): #如果实际输出等于期望输出，模型收敛，循环结束
print('Finished')
print('epoch:',n)
break
#正样本
x1 = [3,4]
y1 = [3,3]
#负样本
x2 = [1]
y2 = [1]
#计算分界线的斜率以及截距
k = -W[1]/W[2]
d = -W[0]/W[2]
print('k=',k)
print('d=',d)
xdata = np.linspace(0,5)
plt.figure()
plt.plot(xdata,xdata*k+d,'r')
plt.plot(x1,y1,'bo')
plt.plot(x2,y2,'yo')
plt.show()五、预习一下多层感知机
1. 相比于单层感知器，多层感知机增加了隐藏层(hidden layer)；
隐藏层, 不包括输入层和输出层，在输入层和输出层中间的所有N层神经元就称作隐藏层！通常输入层不算作神经网络的一部分，对于有一层隐藏层的神经网络，叫做单隐层神经网络或二层感知机；对于第L个隐层，通常有以下一些特性：
a) L层的每一个神经元与 L-1 层的每一个神经元的输出相连；
b) L层的每一个神经元互相没有连接；
2. 引入了新的非线性激活函数(sigmoid/tanh/relu/swish/prelu等)
3. 反向传播算法(back propagation)
4. 优化算法(梯度下降，随机梯度下降，mini-batch)