LeetCode：1631.最小体力消耗路径——中等

题目

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights [ row ][ col ] 表示格子 ( row, col ) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。

实例1

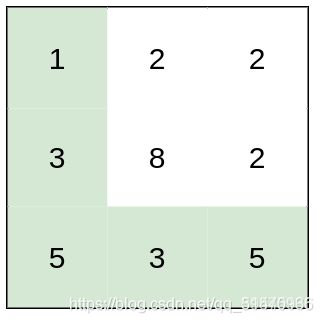
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

实例2：

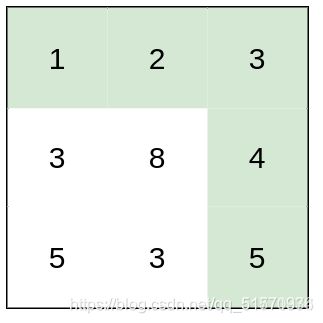
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

实例3

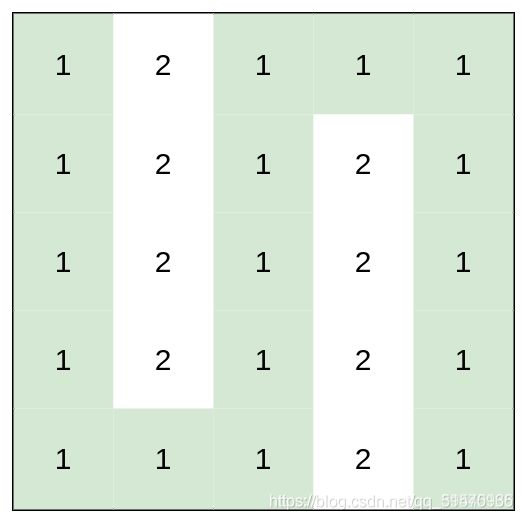
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示

• rows == heighs.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

思路

开始先获取一开始的行列start_row,start_col,然后有四种方向可以进行移动，计算四种移动后的值用cur_row,cur_col来表示，然后判断移动后的变量cur_row,cur_col是否在这个题目矩阵中，如果在的话就计算体力消耗值consume，消耗值的计算是用到当前行列减去一开始行列的绝对值，以及一开始行列的体力消耗值，二者选择一个大的赋值给consume,之所以这么做是因为体力消耗值由高度差绝对值的最大值决定，需要维护这么一个最大值表示走到该点需要的最大体力值，所以需要在该点之前的点和该点之前的点到该点相减绝对值中选择一个大的。接着就遇到了一个判断，如果当前的行列是到了右下角，且这次计算的体力消耗值要小于结果，就更新res。如果不是右下角的，那么就判断这次计算的体力消耗值是否要比dp对应的当前行列小，如果更小就更新dp行列对应的体力消耗值，然后将当前的行列加入列表中。当全部计算完了，输出res就可以了。

代码

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        row , col = len(heights),len(heights[0])  #行和列
        if row == 1 and col == 1: return 0  #行列都为1输出0就可以了，后面行列为1会输出"float(inf)"导致出错
        dp = [[float("inf")]*col for _ in range(row)]  #初始化一个二维矩阵
        dp[0][0] = 0  #0行0列开始，体力消耗值为0
        moves = [[-1,0],[0,-1],[1,0],[0,1]]  #四种不同的方向左上右下
        res = float("inf")  #左上角到右下角的最小体力消耗值
        queue = [[0,0]]  #初始化一个列表，表示当前位置的行列
        while queue:
            start_row,start_col = queue.pop(0)
            for left,right in moves:
                cur_row,cur_col = start_row+left,start_col+right
                if 0 <= cur_row < row and 0 <= cur_col < col:
                    consume = max(abs(heights[cur_row][cur_col]-heights[start_row][start_col]),dp[start_row][start_col])
                    if cur_row == row-1 and cur_col == col -1 and consume < res:
                        res = consume
                    elif consume < dp[cur_row][cur_col]:
                        dp[cur_row][cur_col] = consume
                        queue.append([cur_row,cur_col])
        return res