快速计算每个学生成绩最相似的10个学生（万级别数据量）

作者：小小明

10年编码经验，熟悉Java、Python和Scala，非常擅长解决各类复杂数据处理的逻辑，各类结构化与非结构化数据互转，字符串解析匹配等等。

至今已经帮助至少百名数据从业者解决工作中的实际问题，如果你在数据处理上遇到什么困难，欢迎评论区与我交流。

求每个学生分数最接近的10个学生

需求背景

某MOOC课程网站的老师需要统计每个学生成绩最相近的10个学生，距离计算公式是每门课程的成绩之差的绝对值求和。

例如，学生1的成绩为(83,84,86,99,87)，学生2的成绩为(83,84,86,99,87)

两个学生的距离为|83-83|+|84-84|+|86-86|+|99-99|+|87-87|=0则判定为这两个学生成绩距离完全相同，这个距离越大说明两个学生的成绩差异越大。

为了保护学生隐私，下面仅使用模拟数据展示。

首先读取数据：

import pandas as pd
import numpy as np
import heapq

df = pd.read_csv("学生成绩.csv", encoding="gbk")
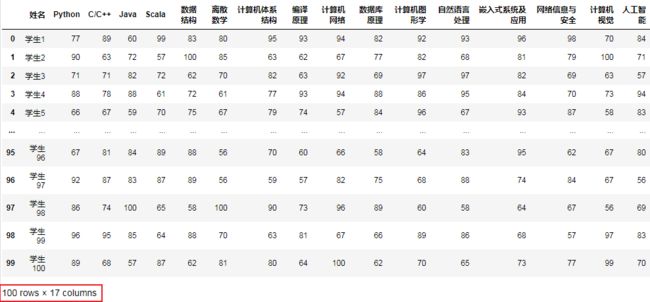
df.head()

结果：

这位老师管理的小班，仅100个学生。

采用双重for循环遍历每个学生与其他99个学生进行匹配计算，也仅1万次循环的计算量，下面我将采用双重for循环进行笛卡尔积计算，遍历出每个学生分数最接近的10个学生。

笛卡尔积+最小堆解决需求

data = df.values
length = data.shape[0]
result = []
for i in range(length):
    # 遍历取出每一行的数据
    src = data[i]
    # 分别取出姓名和成绩列表
    src_name, src_scores = src[0], src[1:]
    # 用一个最小堆保存最接近的10学生
    min_similar_10 = []
    for j in range(length):
        if i == j:
            # 跳过对自己的比较
            continue
        find = data[j]
        # 被比较的学生姓名和成绩
        find_name, find_scores = find[0], find[1:]
        # 计算两个学生成绩的距离
        sim_value = np.abs(src_scores-find_scores).sum()
        # 将当前学习和最小距离保存到最小堆中
        heapq.heappush(min_similar_10, (find_name, sim_value))
        if len(min_similar_10) > 10:
            # 只保留10个距离最小的学生
            min_similar_10 = heapq.nsmallest(
                10, min_similar_10, key=lambda x: x[1])
    name_similars, distances = list(zip(*min_similar_10))
    result.append((src_name, name_similars, distances))
result = pd.DataFrame(result, columns=["姓名", "分数最接近的10个学生", "距离"])
result

最终结果：

仅耗时200毫秒以内，说明笛卡尔积在100数据量时，可以顺利解决这个问题的。

下面简单介绍一下最小堆：

堆是数据结构中最常见的一种数据结构，是一个完全二叉树。最小堆中每一个节点的值都小于等于其子树中每个节点的值。

具体的原理，学过数据结构的读者都懂，没有学过的也不用深究，只需要知道它能够实现快速找到N个最小值。

基于最小堆去保留最小的N个数据，远比排序后取前N个快，几乎就是logN算法复杂度和nlogN算法复杂度的差异。

官方文档：https://docs.python.org/zh-cn/3/library/heapq.html?highlight=heapq#module-heapq

实现源码：https://github.com/python/cpython/blob/3.9/Lib/heapq.py

如果你确实对堆的实现原理很感兴趣，可以参考我的数据结构学习笔记：

https://datastructure.xiaoxiaoming.xyz/#/16.%E5%A0%86

使用numpy向量化操作解决需求

好景不长，该MOOC网站的管理员觉得我的代码处理的效果比较好，希望把历史班级所有学生的分数最接近的10个学生都找出来，大概有1W以上的学生。

用我上面的代码跑了一下，结果跑了10分钟也没能计算完，问我能不能优化一下代码。其实10分钟跑不完太正常了，之前100个学生其实只需要循环大概1万次，而这次1万个学生却需要循环大概1亿次，耗时差距接近1万倍，当然如果他再多等等，20分钟也能跑完。

不过我个人也无法容忍要等那么久，经过我一番代码优化，程序在2分钟内对1万条数据跑出了结果。

考虑到部分很多读者都没有看懂上面的操作，这次我将用一个简单的方法分步拆解，而且代码更短，性能更高。

直接对本文开头的100条数据进行测试，首先获取源数据的姓名和分数数组：

data = df.values
length = data.shape[0]
names = data[:, 0]
scores = data[:, 1:]
print(names[:5])
print(scores[:5])

结果：

['学生1' '学生2' '学生3' '学生4' '学生5']
[[71 82 81 84 73 95 62 96 96 87 61 78 79 89 98 80]
 [57 91 99 74 93 93 58 74 89 84 63 62 78 57 94 74]
 [72 59 76 60 99 71 73 74 72 74 85 79 100 88 80 91]
 [71 62 81 80 57 84 92 95 63 59 84 64 90 58 60 75]
 [83 62 95 76 57 75 97 57 65 63 84 73 74 59 62 93]]

测试对第一个学生求分数最接近的10个学生：

for i in range(length):
    name, score = names[i], scores[i]
    print(name, score)
    break

结果：

学生1 [77 89 60 99 83 80 95 93 94 82 92 93 96 98 70 84]

利用numpy向量化操作一次性求出该学生与其他所有学生的距离：

score_diff = np.abs(scores-score).sum(axis=1)
score_diff

结果：

array([0, 322, 248, 203, 215, 366, 198, 224, 299, 229, 274, 240, 253, 238,
       183, 239, 223, 344, 320, 221, 291, 264, 273, 309, 307, 243, 258,
       231, 225, 185, 234, 324, 315, 247, 247, 232, 179, 210, 238, 261,
       175, 252, 259, 254, 330, 270, 193, 248, 252, 214, 175, 219, 262,
       256, 265, 249, 263, 180, 270, 294, 260, 195, 272, 240, 213, 181,
       252, 292, 261, 233, 238, 205, 237, 241, 244, 234, 255, 151, 228,
       241, 173, 174, 221, 248, 191, 249, 243, 224, 252, 266, 229, 231,
       228, 346, 232, 273, 269, 336, 294, 277], dtype=object)

取出距离最短的11个学生的索引，然后删除自身的索引：

min_similar_index = np.argpartition(score_diff, 11)[:11].tolist()
min_similar_index.remove(i)
min_similar_index

结果：

[77, 80, 81, 40, 50, 36, 57, 65, 14, 29]

根据这10个学生的索引读取所需要的数据：

name_similars = names[min_similar_index]
distances = score_diff[min_similar_index]
print(name_similars)
print(distances)

结果：

['学生78' '学生81' '学生82' '学生41' '学生51' '学生37' '学生58' '学生66' '学生15' '学生30']
[151 173 174 175 175 179 180 181 183 185]

这样我们就已经计算出该学生成绩最解决的10个学生的姓名和距离。

下面我整理一下完整处理代码：

data = df.values
length = data.shape[0]
names = data[:, 0]
scores = data[:, 1:]

result = []
for i in range(length):
    name, score = names[i], scores[i]
    score_diff = np.abs(scores-score).sum(axis=1)
    min_similar_index = np.argpartition(score_diff, 11)[:11].tolist()
    min_similar_index.remove(i)
    name_similars = names[min_similar_index]
    distances = score_diff[min_similar_index]
    result.append((name, name_similars, distances))
result = pd.DataFrame(result, columns=["姓名", "分数最接近的10个学生", "距离"])
result

结果：

下面再针对一万条数据跑一跑：

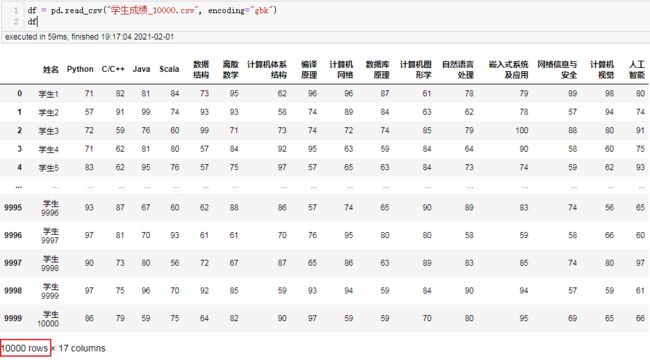
df = pd.read_csv("学生成绩_10000.csv", encoding="gbk")
data = df.values
length = data.shape[0]
names = data[:, 0]
scores = data[:, 1:]

result = []
for i in range(length):
    name, score = names[i], scores[i]
    score_diff = np.abs(scores-score).sum(axis=1)
    min_similar_index = np.argpartition(score_diff, 11)[:11].tolist()
    min_similar_index.remove(i)
    name_similars = names[min_similar_index]
    distances = score_diff[min_similar_index]
    result.append((name, name_similars, distances))
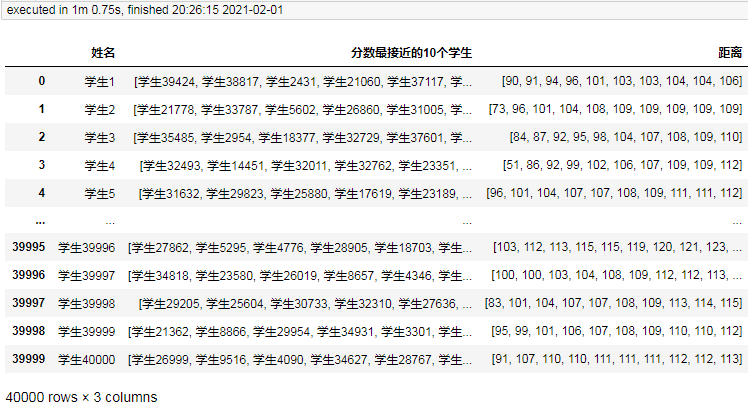
result = pd.DataFrame(result, columns=["姓名", "分数最接近的10个学生", "距离"])
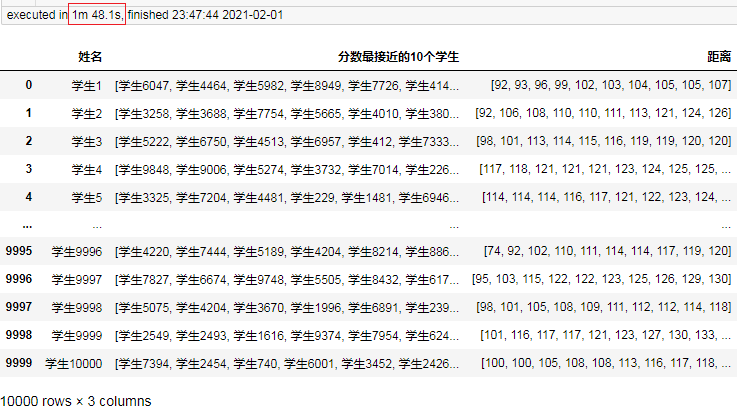
result

结果：

可以看到耗时为1分48秒。

使用ball_tree解决需求

虽然上面的优化已经大幅度提升了程序性能，但毕竟仍然是O(n^2)算法复杂度的方法，万一哪天网站要求对10万个学生计算呢？时间又要多翻了接近几十倍，耗时可能达到好几个小时。我转而一想直接用KNN内部的ball_tree来解决这个问题吧。

（关于使用KNN查找最近点的问题可参考很早之前的一篇文章：https://blog.csdn.net/as604049322/article/details/112385553）

先使用1000条学生成绩的数据进行测试，读取这1000条学生成绩数据：

df = pd.read_csv("学生成绩_1000.csv", encoding="gbk")
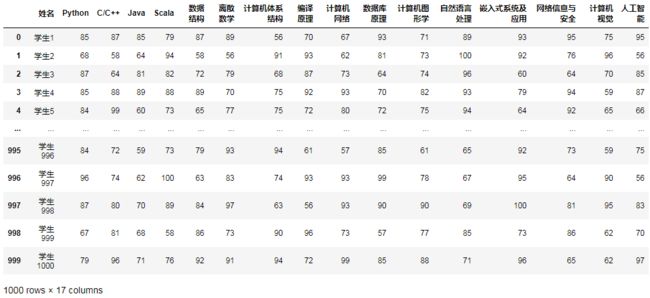
df

结果：

然后我们取出需要被训练的数据：

# 取出用于被KNN训练的数据
data = df.iloc[:, 1:].values
# y本身用于标注每条数据属于哪个类别，但我并不使用KNN的分类功能，所以统一全部标注为类别0
y = np.zeros(data.shape[0], dtype='int8')
print(data[:5])
print(y[:5])

结果：

[[ 77  89  60  99  83  80  95  93  94  82  92  93  96  98  70  84]
 [ 90  63  72  57 100  85  63  62  67  77  82  68  81  79 100  71]
 [ 71  71  82  72  62  70  82  63  92  69  97  97  82  69  63  57]
 [ 88  78  88  61  72  61  77  93  94  88  86  95  84  70  73  94]
 [ 66  67  59  70  75  67  79  74  57  84  96  67  93  87  58  83]]
[0 0 0 0 0]

创建KNN训练器，并进行训练：

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier(n_neighbors=1, algorithm='ball_tree', p=1)
knn.fit(data, y)
distance, similar_points = knn.kneighbors(
    data, n_neighbors=11, return_distance=True)
distance = distance.astype("int", copy=False)
print(distance[:5])
print(similar_points[:5])

结果：

这个过程的耗时仅50毫秒，几乎可以忽略不计。

n_neighbors是KNN用来分类的参数，我并不使用它，将其指定的越小，越能减少无用的计算量，但是必须比0大，所以我指定为1。

而需求方要求的距离计算公式显然就等价于曼哈顿距离，所以我将p指定为1，就跟需求方要求的距离计算公式一致。

knn.kneighbors则用来计算最近的点，n_neighbors指定为11是因为结果会包含自身，我打算后面再去除。

由于sklearn最终计算出来的距离是float浮点数类型，而我们的需求只可能产生整数距离，所以我将其转换为整数。

上面其实就相当于已经计算出了结果，下面我再将结果整理成需要的格式即可：

names = df['姓名']
result = []
for i, name in names.iteritems():
    name_similar_indexs = similar_points[i].tolist()
    self_index = name_similar_indexs.index(i)
    name_similar_indexs.pop(self_index)
    name_similars = names[name_similar_indexs].tolist()
    distances = distance[i].tolist()
    distances.pop(self_index)
    result.append((name, name_similars, distances))
result = pd.DataFrame(result, columns=["姓名", "分数最接近的10个学生", "距离"])
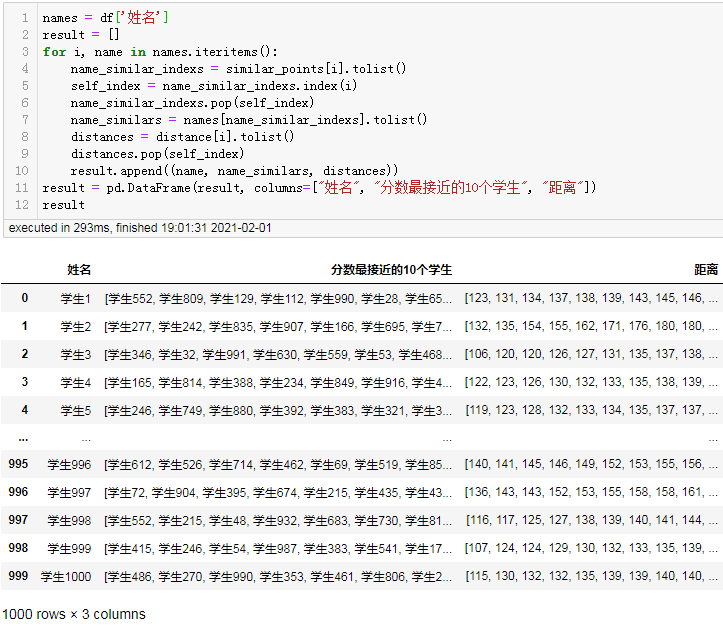
result

结果：

对于1000条数据ball_tree的计算耗时为毫秒级。

下面我们对一万条学生成绩数据进行计算，首先读取数据：

df = pd.read_csv("学生成绩_10000.csv", encoding="gbk")
df

结果：

完整计算代码：

# 取出用于被KNN训练的数据
from sklearn.neighbors import KNeighborsClassifier
data = df.iloc[:, 1:].values
# y本身用于标注每条数据属于哪个类别，但我并不使用KNN的分类功能，所以统一全部标注为类别0
y = np.zeros(data.shape[0], dtype='int8')

knn = KNeighborsClassifier(n_neighbors=1, algorithm='ball_tree', p=1)
knn.fit(data, y)
distance, similar_points = knn.kneighbors(
    data, n_neighbors=11, return_distance=True)
distance = distance.astype("int", copy=False)

names = df['姓名']
result = []
for i, name in names.iteritems():
    name_similar_indexs = similar_points[i].tolist()
    self_index = name_similar_indexs.index(i)
    name_similar_indexs.pop(self_index)
    name_similars = names[name_similar_indexs].tolist()
    distances = distance[i].tolist()
    distances.pop(self_index)
    result.append((name, name_similars, distances))
result = pd.DataFrame(result, columns=["姓名", "分数最接近的10个学生", "距离"])
result

结果：

可以看到1万条数据ball_tree仅仅5秒就计算完了。

对4万条学生数据测试

为了测试方便，不再用excel来生成数据，而是直接使用python。

python直接生成测试数据的方法，以生成10条数据为例：

size = 100000

data = np.c_[np.arange(1, size+1).reshape((-1, 1)),
             np.random.randint(56, 101, size=(size, 16))]
df = pd.DataFrame(data, columns=["姓名", "Python", "C/C++", "Java", "Scala", "数据结构", "离散数学",
                                 "计算机体系结构", "编译原理", "计算机网络", "数据库原理", "计算机图形学",
                                 "自然语言处理", "嵌入式系统及应用", "网络信息与安全", "计算机视觉", "人工智能"])
df["姓名"] = "学生"+df["姓名"].astype(str)
df

结果：

然后使用上面相同的代码分别测试1w条、2w条、3w条、…、10w条：

1万条耗时5.3秒。

2万条耗时15.8秒。

3万条耗时32.3秒。

4万条耗时60.75秒。

预估10万条数据的耗时

这不行，仅4万条耗时就达到一分钟，这也开始让我有点等的捉急了，不能继续测试下去了。

这时间增长趋势好像也不是线性增长而是指数增长，下面先就记录一下多少条记录时耗时多久吧：

import pandas as pd
import numpy as np
import time
from sklearn.neighbors import KNeighborsClassifier

times = {
     }
for size in np.r_[np.arange(1000, 10001, 1000), np.arange(20000, 40001, 10000)]:
    data = np.c_[np.arange(1, size+1).reshape((-1, 1)),
                 np.random.randint(56, 101, size=(size, 16))]
    df = pd.DataFrame(data, columns=["姓名", "Python", "C/C++", "Java", "Scala", "数据结构", "离散数学",
                                     "计算机体系结构", "编译原理", "计算机网络", "数据库原理", "计算机图形学",
                                     "自然语言处理", "嵌入式系统及应用", "网络信息与安全", "计算机视觉", "人工智能"])
    df["姓名"] = "学生"+df["姓名"].astype(str)

    start_time = time.perf_counter()
    # 取出用于被KNN训练的数据
    data = df.iloc[:, 1:].values
    # y本身用于标注每条数据属于哪个类别，但我并不使用KNN的分类功能，所以统一全部标注为类别0
    y = np.zeros(data.shape[0], dtype='int8')

    knn = KNeighborsClassifier(n_neighbors=1, algorithm='ball_tree', p=1)
    knn.fit(data, y)
    distance, similar_points = knn.kneighbors(
        data, n_neighbors=11, return_distance=True)
    distance = distance.astype("int", copy=False)
    names = df['姓名']
    result = []
    for i, name in names.iteritems():
        name_similar_indexs = similar_points[i].tolist()
        self_index = name_similar_indexs.index(i)
        name_similar_indexs.pop(self_index)
        name_similars = names[name_similar_indexs].tolist()
        distances = distance[i].tolist()
        distances.pop(self_index)
        result.append((name, name_similars, distances))
    result = pd.DataFrame(result, columns=["姓名", "分数最接近的10个学生", "距离"])
    take_time = time.perf_counter()-start_time
    print(f"{size}条数据耗时{take_time:.2f}秒")
    times[size] = take_time
time_df = pd.DataFrame.from_dict(times, orient='index', columns=["time"])
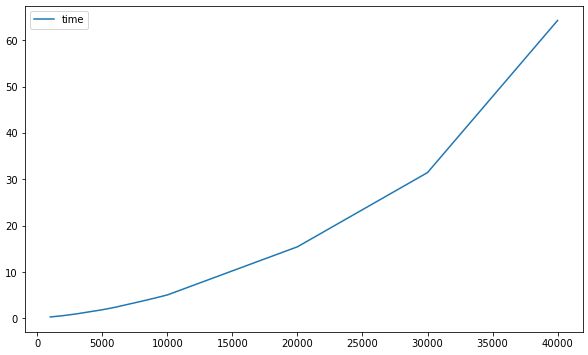
time_df.plot()

结果：

1000条数据耗时0.28秒
2000条数据耗时0.58秒
3000条数据耗时0.94秒
4000条数据耗时1.39秒
5000条数据耗时1.84秒
6000条数据耗时2.38秒
7000条数据耗时3.03秒
8000条数据耗时3.66秒
9000条数据耗时4.34秒
10000条数据耗时5.04秒
20000条数据耗时15.43秒
30000条数据耗时31.44秒
40000条数据耗时64.27秒

从这走势来看有点像二次函数或幂次函数，我们假设这是一个二次函数然后使用numpy拟合这条曲线，并预估10万数据的耗时：

from numpy import polyfit, poly1d
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(1000, 100001, 1000)
y = poly1d(polyfit(time_df.index, time_df.time, 2))

plt.figure(figsize=(10, 6))
plt.plot(time_df.index, time_df.time, 'rx')
plt.plot(x, y(x), 'b:')
plt.show()
print(f"10万条数据预计耗时{y(100000):.2f}秒")

结果：

预计耗时6分钟，但如果这个时候还用笛卡尔积去计算，估计耗时几个小时。

不过实际测试了一下，好像10分钟也没有出结果，看来样本还是太少，曲线拟合的效果还是不太准。

测试到6W试一下：

import pandas as pd
import numpy as np
import time
from sklearn.neighbors import KNeighborsClassifier

times = {
     }
for size in np.r_[np.arange(1000, 10001, 1000), np.arange(20000, 60001, 10000)]:
    data = np.c_[np.arange(1, size+1).reshape((-1, 1)),
                 np.random.randint(56, 101, size=(size, 16))]
    df = pd.DataFrame(data, columns=["姓名", "Python", "C/C++", "Java", "Scala", "数据结构", "离散数学",
                                     "计算机体系结构", "编译原理", "计算机网络", "数据库原理", "计算机图形学",
                                     "自然语言处理", "嵌入式系统及应用", "网络信息与安全", "计算机视觉", "人工智能"])
    df["姓名"] = "学生"+df["姓名"].astype(str)

    start_time = time.perf_counter()
    # 取出用于被KNN训练的数据
    data = df.iloc[:, 1:].values
    # y本身用于标注每条数据属于哪个类别，但我并不使用KNN的分类功能，所以统一全部标注为类别0
    y = np.zeros(data.shape[0], dtype='int8')

    knn = KNeighborsClassifier(n_neighbors=1, algorithm='ball_tree', p=1)
    knn.fit(data, y)
    distance, similar_points = knn.kneighbors(
        data, n_neighbors=11, return_distance=True)
    distance = distance.astype("int", copy=False)
    names = df['姓名']
    result = []
    for i, name in names.iteritems():
        name_similar_indexs = similar_points[i].tolist()
        self_index = name_similar_indexs.index(i)
        name_similar_indexs.pop(self_index)
        name_similars = names[name_similar_indexs].tolist()
        distances = distance[i].tolist()
        distances.pop(self_index)
        result.append((name, name_similars, distances))
    result = pd.DataFrame(result, columns=["姓名", "分数最接近的10个学生", "距离"])
    take_time = time.perf_counter()-start_time
    print(f"{size}条数据耗时{take_time:.2f}秒")
    times[size] = take_time
time_df = pd.DataFrame.from_dict(times, orient='index', columns=["time"])

结果：

1000条数据耗时0.29秒
2000条数据耗时0.59秒
3000条数据耗时0.98秒
4000条数据耗时1.40秒
5000条数据耗时1.97秒
6000条数据耗时2.44秒
7000条数据耗时3.00秒
8000条数据耗时3.74秒
9000条数据耗时4.41秒
10000条数据耗时5.23秒
20000条数据耗时15.92秒
30000条数据耗时31.75秒
40000条数据耗时64.25秒
50000条数据耗时132.26秒
60000条数据耗时220.87秒

再拟合一下：

from numpy import polyfit, poly1d
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(1000, 100001, 1000)
y = poly1d(polyfit(time_df.index, time_df.time, 2))

plt.figure(figsize=(10, 6))
plt.plot(time_df.index, time_df.time, 'rx')
plt.plot(x, y(x), 'b:')
plt.show()
print(f"10万条数据预计耗时{y(100000):.2f}秒")

结果：

从拟合效果来看，可能这个虚线实际并不是二次函数，而是3次以上的函数，下面使用3次函数进行拟合：

from numpy import polyfit, poly1d
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(1000, 100001, 1000)
y = poly1d(polyfit(time_df.index, time_df.time, 3))

plt.figure(figsize=(10, 6))
plt.plot(time_df.index, time_df.time, 'rx')
plt.plot(x, y(x), 'b:')
plt.show()
print(f"10万条数据预计耗时{y(100000):.2f}秒")

结果：

预估耗时为17分钟。

实际耗时呢？

import pandas as pd
import numpy as np
from sklearn.neighbors import KNeighborsClassifier

size = 100000
data = np.c_[np.arange(1, size+1).reshape((-1, 1)),
             np.random.randint(56, 101, size=(size, 16))]
df = pd.DataFrame(data, columns=["姓名", "Python", "C/C++", "Java", "Scala", "数据结构", "离散数学",
                                 "计算机体系结构", "编译原理", "计算机网络", "数据库原理", "计算机图形学",
                                 "自然语言处理", "嵌入式系统及应用", "网络信息与安全", "计算机视觉", "人工智能"])
df["姓名"] = "学生"+df["姓名"].astype(str)
# 取出用于被KNN训练的数据
data = df.iloc[:, 1:].values
# y本身用于标注每条数据属于哪个类别，但我并不使用KNN的分类功能，所以统一全部标注为类别0
y = np.zeros(data.shape[0], dtype='int8')

knn = KNeighborsClassifier(n_neighbors=1, algorithm='ball_tree', p=1)
knn.fit(data, y)
distance, similar_points = knn.kneighbors(
    data, n_neighbors=11, return_distance=True)
distance = distance.astype("int", copy=False)
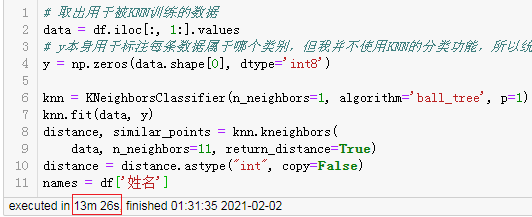
names = df['姓名']

结果：

训练耗时13分钟。

from tqdm.notebook import tqdm

result = []
pbar = tqdm(total=size)
for i, name in names.items():
    pbar.update(1)
    name_similar_indexs = similar_points[i].tolist()
    self_index = name_similar_indexs.index(i)
    name_similar_indexs.pop(self_index)
    name_similars = names[name_similar_indexs].tolist()
    distances = distance[i].tolist()
    distances.pop(self_index)
    result.append((name, name_similars, distances))
pbar.close()
result = pd.DataFrame(result, columns=["姓名", "分数最接近的10个学生", "距离"])
result

整理结果耗时半分钟，实际耗时是14分钟，跟预测的17分钟差不多。

虽然14分钟也比较慢，但相对前面的笛卡尔积的算法需要耗时好几小时而言已经大幅度提升程序计算性能，节约了计算时间。

总结

今天我向你演示了如何使用最小堆和numpy来快速计算每个学生分数最接近的10个学生，可以看到在数据量小于10000时，这种时间复杂度为O(n^2)的算法还可以接受，但一旦达到2万以上，基本上就慢的难以忍受了。所以我使用ball_tree来计算这个距离，1W数据量仅耗时5秒。

但是当数据量达到5万以上时，ball_tree也有点慢了，但也相对笛卡尔积的算法还是快了很多。

最后，我使用numpy拟合时间曲线，预估10w数据量时ball_tree的耗时为17分钟，实际测试是14分钟，基本预测正确。

欢迎下方留言或评论，分享你的看法。