python汉诺塔_python实现数据结构与算法之递归绘制汉诺塔解法
简介
汉诺塔问题源于印度一个古老传说。相传大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。
汉诺塔问问题是法国数学家爱德华·卢卡斯于1883年发现的。他受到一个关于印度教寺庙的传说的启发,故事中这一问题交由年轻僧侣们解决。最开始,僧侣们得到三根杆子,64个金圆盘堆叠在其中一根上, 每个圆盘比其下的小一点。僧侣们的任务是将64个圆盘从一根杆上转移到另一根杆上,但有两项重要的限制,一是他们一次只能移动一个圆盘,一是不能将大圆盘放在小圆盘之上。僧侣们日以继夜地工作,每秒移动一个圆盘。传说中,当工作完成之时寺庙就会崩塌, 世界则将不复存在。
解决思路
我们如何用递归解决这个问题呢?我们又如何完全解决这一类问题?基本情况又是什么?让我们从递归调用的最底端入手。假设你有一个五个圆盘组成的塔,最开始在一号杆上。如果你已经知道如何将有四个圆盘的小塔从一号杆移到二号杆,就可以很容易地将第五个圆盘移动到三号杆,然后将四个圆盘的塔从二号杆移动到三号杆。但是如果你不知道如何移动有四个圆盘的塔呢?这时又假设你知道如何将有三个圆盘的塔移到三号杆;然后你就可以将第四个圆盘移动到二号杆,然后再将位于三号杆的有三个圆盘的塔移到其上。但是如果你不知道如何移动有三个圆盘的小塔又怎么办呢?那考虑先将有两个圆盘的小塔移动到二号杆,再将第三个圆盘移动到三号杆,最后将两个圆盘的小塔移动到三号杆会如何呢?但如果你连这个也不会,该如何处理?显然你知道将单个圆盘移到三号杆十分简单甚至可以说无需思考,似乎这就是这一问题最基础的部分。
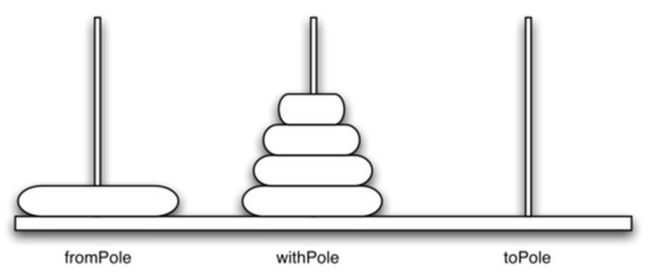
汉诺塔问题
下面是关于将塔经由中间杆,从起始杆移到目标杆的抽象概述:
把圆盘数减一层数的小塔经过目标杆移动到中间杆;
把剩下的圆盘移动到目标杆;
把圆盘数减一层数的小塔从中间杆,经过起始杆移动到目标杆。
只要我们一直遵循大的圆盘保持在底层的规则,我们就能用以上的三步来递归, 很容易地处理任意多圆盘的问题。
Python代码实现
# 代码递归实现汉诺塔问题,使用栈来存储
import turtle
class Stack:
"""栈的实现"""
def __init__(self):
self.items = []
def is_empty(self):
return self.size() == 0
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.is_empty():
return self.items[-1]
def size(self):
return len(self.items)
def draw_poles():
"""
画出汉诺塔的三个柱子
:return:
"""
t = turtle.Turtle()
t.hideturtle()
for i in range(3):
t.up()
t.pensize(10)
t.speed(100)
t.goto(200*(i-1), 100)
t.down()
t.goto(200*(i-1), -100)
t.goto(200*(i-1)-20, -100)
t.goto(200*(i-1)+20, -100)
def create_plates(n):
"""
制造盘子
:param n: 制造盘子个数
:return: 盘子存储的列表
"""
plates = [turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].color("brown")
plates[i].pencolor("black")
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(1,8-i)
plates[i].goto(-200,-90+20*i)
plates[i].showturtle()
return plates
def pole_stack():
"""
制造poles的栈
:return: 三个柱子的栈
"""
poles = [Stack() for i in range(3)]
return poles
def move_disk(plates,poles,fp,tp):
"""
移动起始柱子的最顶端的盘子到目的柱子
:param plates: 盘子列表
:param poles: 柱子的栈列表
:param fp: 起始柱子的索引
:param tp: 移动到目的柱子的索引
:return:
"""
mov = poles[fp].peek()
plates[mov].goto((fp-1)*200, 150)
plates[mov].goto((tp-1)*200, 150)
# 确定移动到底部的高度,确保恰好放在原来最上面的盘子上面
l = poles[tp].size()
plates[mov].goto((tp-1)*200, -90+20*l)
def move_tower(plates,poles,n,from_pole,to_pole,with_pole):
"""
递归放盘子
:param plates: 盘子列表
:param poles: 柱子列表
:param n: 盘子个数
:param from_pole: 起始柱子索引
:param to_pole: 目的柱子索引
:param with_pole: 中间柱子索引
:return:
"""
if n >= 1:
# 从起始柱子移动顶部n-1个盘子到中间柱子
move_tower(plates, poles,n-1,from_pole,with_pole,to_pole)
# 将最底下的那个盘子从起始柱子移动到目的柱子
move_disk(plates,poles,from_pole,to_pole)
poles[to_pole].push(poles[from_pole].pop())
#从中间柱子移动顶部n-1个盘子到目的柱子,完成移动
move_tower(plates,poles,n-1,with_pole,to_pole,from_pole)
# 测试数据
if __name__ == '__main__':
screen = turtle.Screen()
n = 8 # 创建盘子个数
draw_poles()
plates = create_plates(n)
poles = pole_stack()
# 将盘子放在起始柱子
for i in range(n):
poles[0].push(i)
move_tower(plates,poles,n,0,2,1)
screen.exitonclick()
动画演示
汉诺塔问题求解动画演示
联系我们
个人博客网站:http://www.bling2.cn/
Github地址:https://github.com/lb971216008/Use-Python-to-Achieve
知乎专栏:https://zhuanlan.zhihu.com/Use-Python-to-Achieve
小专栏:https://xiaozhuanlan.com/Use-Python-to-Achieve
博客园:https://www.cnblogs.com/Use-Python-to-Achieve
扫码关注公众号【不灵兔】,获取更多免费资源~~~
更多内容
专辑——python实现之排序算法
python实现·十大经典排序算法之冒泡排序
python 实现·十大经典排序算法之选择排序
python实现·十大经典排序算法之插入排序
python实现·十大经典排序算法之快速排序
python实现·十大经典排序算法之归并排序
python实现·十大经典排序算法之希尔排序
python实现·十大经典排序算法之堆排序
python实现·十大经典排序算法之计数排序
python实现·十大排序经典算法之基数排序
python实现·十大经典排序算法之桶排序
免费资源
Python电子书资源分享(20200605更新)
好用的软件分享
IT学习视频分享