我的算法不可能这么简单—单调栈

题目

洛谷 ： P5788 【模板】单调栈

众所周知有了神就有了光，有了梦想就有了动力，有了lbw就有了牛 ，咳咳， 有了单调队列就有单调栈。

如果你还不了解单调队列，可以前往->我的算法不可能这么简单—单调队列

• 这两个东西有异曲同工之妙！

暴力做法

• 诶，读完题(这不是个大水题吗，看我直接干了它)

• ？n<=3×10⁶ 打扰了打扰了。。。

• 先把暴力思想水了，然后与单调栈进行比较一下：

#include 
using namespace std;
#define int long long

int a[3000006],n;

signed main(){
     
    scanf("%lld",&n);
    for(int i=1;i<=n;++i)
        scanf("%lld",&a[i]);

    for(int i=1;i<=n;++i){
     
        bool flag = false;
        for(int j=i+1;j<=n;++j)
            if(a[j]>a[i]){
     
                printf("%lld ",j);
                flag=true;
                break;
            }
        if(!flag) printf("0 ");
    }

    return 0;
}

我相信你们都能写出来暴力代码。

T了四个点。

• 下面我们介绍单调栈来做了它

单调栈

结合单调队列，我们可以很快知道这玩意应该存的也是一个单调递增或者单调递减的值的下标 。

这题是单调递增栈。。从栈顶往栈底看是单调递增的。既然如此，我们仍然跟单调队列一样，采用数组模拟栈：

int Stack[3000006],top;//Stack为我们的栈，top代表栈顶

• 类比单调队列，我们不难想到，我们应该让栈底始终保持最大值，如果新来的值比栈顶元素小，那么便直接插入栈顶，如果比栈顶元素大，那么直接删除栈顶，循环直到遇到一个大于新元素的值或者栈为空为止。
• 而且我们发现单调栈没有有效期，它不像单调队列那样，窗口会往后面滑，导致队首元素过期，所以我们不必考虑栈底元素需不需要删除的问题。也因此我们只放置了一个 top 变量记录栈顶。

我们先画个图分析一下：

• 我们从左往右看，1的第一个最大值显然是4，如果我们让 1 先进栈，那么下一个进栈的4会将1顶出去。所以。。。
• 所以我们怎么判断1后面第一个大于1的元素值是4的？好像并不能判断。。。
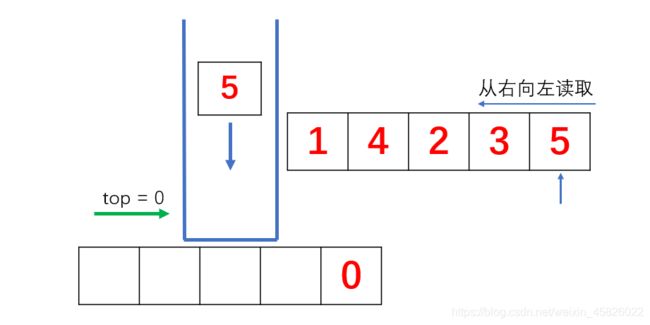
• 既然从左到右看，没法干成，那么我们从右往左看一下试试。
• 我们先让5进栈，下一个元素3，发现当前栈顶是5，而且5正好是3后面的第一个大值。
• 我们让3进栈，下一个元素2，发现当前栈顶是3，而且3正好是2后面的第一个大值。
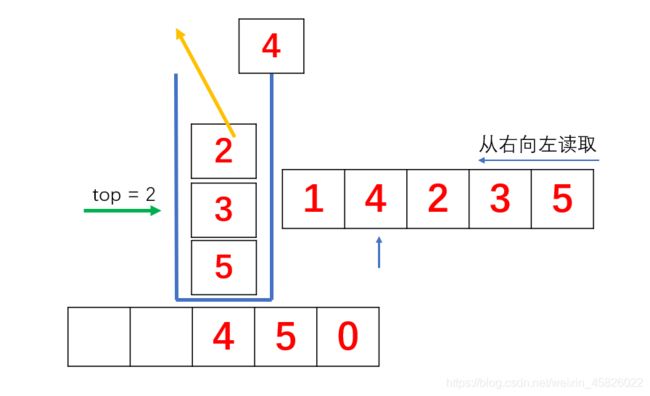
• 我们让2进栈，下一个元素4，4比栈顶的2大，我们让2出栈，栈顶变成3，依旧让3出栈，然后栈顶变成5，4比5小，而且4后面的第一大值就是当前栈顶5！
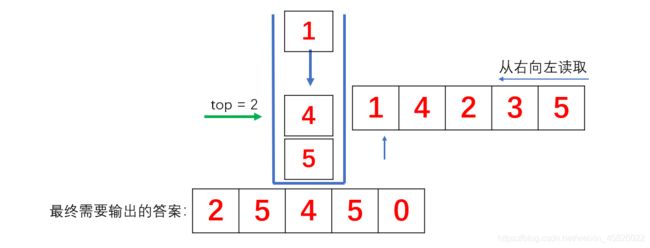
• 最后我们让4进栈，下一个元素1，显然1后面的第一大值就是当前栈顶4！！！

• 我们以图的形式再次形象的分析一遍上述过程，因为这个过程就是代码的实现步骤！

• 5是最后一个元素了诶，当前栈为空，那么我们直接记录栈顶元素0，5入栈。

• 下一个元素为3，3比栈顶元素5小，直接记录栈顶元素5的下标5，3入栈。

• 下一个元素为2，比栈顶元素3小，记录栈顶元素3的下标4 ， 2入栈。

• 下一个元素为4，4比栈顶元素2大，将栈顶元素2出栈

• 同理，栈顶元素2出栈后，3成为新栈顶，依旧比4小，继续出栈，下一个栈顶5比4大，记录栈顶元素5的下标5，4入栈。

• 最后新元素1，比当前栈顶元素4小，记录栈顶元素4的下标2，1入栈。

• 最后我们只需将记录的答案从左往右输出一遍即可。
• 再次注意我们每次记录的是元素对应的下标，不是记录的元素值！这里图里面写值的原因是我们方便去进行比较，只是为了方便我们肉眼去比较而已，在写算法的时候，栈里面存储的是元素下标！

例题代码

经过上面的分析，我相信代码的实现已经不是困难的事情

#include 
using namespace std;
#define int long long

int a[3000006],n;
int Stack[3000006],top;
int ans[3000006];//记录答案

signed main(){
     
    scanf("%lld",&n);
    for(int i=1;i<=n;++i)
        scanf("%lld",&a[i]);

    //从右往左看 从n到1
    for(int i=n;i>=1;--i){
     
        //如果新元素比栈顶元素大，弹出栈顶元素
        while(top && a[Stack[top]]<=a[i]) top--;
        //记录当前栈顶元素
        ans[i] = Stack[top];
        //新元素的下标入栈
        Stack[++top] = i;
    }

    for(int i=1;i<=n;++i)
        printf("%lld ",ans[i]);

    return 0;
}

我们其实可以发现，单调栈的代码非常非常非常短。。。然后就绿了这道题。

额外经验

P2947 [USACO09MAR]Look Up S

• 这题堪比模板题，我们只是将模板的空格输出换成换行输出就可以AC

#include 
using namespace std;
#define int long long

const int maxn = 1e5+9;

int a[maxn],n;
int Stack[maxn],top;
int ans[maxn];

signed main(){
     
    scanf("%lld",&n);
    for(int i=1;i<=n;++i)
        scanf("%lld",&a[i]);

    for(int i=n;i>=1;--i){
     
        while(top&&a[Stack[top]]<=a[i]) top--;
        ans[i] = Stack[top];
        Stack[++top] = i;
    }

    for(int i=1;i<=n;++i)
        printf("%lld\n",ans[i]);

    return 0;
}

P1901 发射站

• 这个题刚开始可能不太好想，但是画画图还是可以看出来的。

#include 
using namespace std;
#define int long long

const int maxn = 1e6+9;

int h[maxn],v[maxn],n;
int Stack[maxn],top;
int ans[maxn];

signed main(){
     
    scanf("%lld",&n);
    for(int i=1;i<=n;++i)
        scanf("%lld %lld",&h[i],&v[i]);
    //本题正着，倒着都可以
    for(int i=n;i>=1;--i){
     
        //如果新元素比栈顶元素大，说明这个信号塔把这个信号塔的信号接收了
        while(top && h[Stack[top]]<=h[i]) ans[i]+=v[Stack[top--]];
        //遇到了栈顶元素，此时栈顶元素要么比该信号塔高接受了该信号塔的信号
        //要么就是该元素为栈顶，它的信号没有被任何塔接受到，直接存放到0号位置，不影响结果，因为我们是从1开始的
        ans[Stack[top]] += v[i];
        Stack[++top] = i;
    }
    int res = 0;
    for(int i=1;i<=n;++i)
        res = max(ans[i],res);
    cout<<res;

    return 0;
}

P2866 [USACO06NOV]Bad Hair Day S

• 这道题必须从左往右扫，因为我们要用到栈内元素的个数，所以这题使用 stack 实现。
  如果看不懂，画画图就行。

#include 
using namespace std;
#define int long long

const int maxn = 1e5+9;

int a[maxn],n;
stack<int> s;
int ans[maxn];

signed main(){
     
    scanf("%lld",&n);
    for(int i=1;i<=n;++i)
        scanf("%lld",&a[i]);

    for(int i=1;i<=n;++i){
     
        while(!s.empty() && a[s.top()]<=a[i]) s.pop();
        if(!s.empty())  ans[s.top()] += s.size();
        s.push(i);
    }
    int res = 0;
    for(int i=1;i<=n;++i)
        res += ans[i];
    cout<<res;

    return 0;
}