python 实现马科维茨_财码Python量化选股(四)投资组合
哈里·马科维茨(Harry Markowitz)于1952年提出的“投资组合理论(Portfolio Selection)”包含两个重要内容:均值-方差分析方法和投资组合有效边界模型。
其中均值-方差优化法,将不同预期收益和波动率的资产组合在一起,决定一种数学上最优的分配方案,从而将目标收益的风险降至最低,此类最优投资组合的集合被称为有效边界。
本实验使用PyPortfolioOpt实现投资组合优化。PyPortfolioOpt是基于Markowitz和Black-Litterman等理论开发的金融投资组合优化技术的库,该项目提供了五个主要功能:
预期收益估算(平均历史收益)
风险模型(即资产收益的协方差)
有效边界优化
布莱克-利特曼分配
其他投资组合优化器
关于PyPortfolioOpt,更详细的资料见:https://pyportfolioopt.readthedocs.io/en/latest/
Python案例模拟
1. 安装PyPortfolioOpt。
import pandas as pdimport numpy as npfrom pypfopt import EfficientFrontierfrom pypfopt import risk_modelsfrom pypfopt import expected_returnsimport baostock as bs2. 获取上个实验中我们选出的股票
stock=pd.read_excel(r'选股初探.xlsx') stock['code']3. 获取股票相关数据
因为我们选股用的是2019年12月31日的数据,因此这里往前再分析3年
lg = bs.login()data_list = []for s in stock['code']: rs = bs.query_history_k_data_plus(s, 'date,code,close', start_date='2016-01-01', end_date='2019-12-31', adjustflag='2') while (rs.error_code == '0') & rs.next(): data_list.append(rs.get_row_data())df = pd.DataFrame(data_list, columns=rs.fields)df = df.apply(pd.to_numeric, errors='ignore')df['date']=pd.to_datetime(df['date'])bs.logout()df4. 处理数据
索引应包含日期或时间戳,每列应代表资产价格的历史值。
lg = bs.login()data_list = []for s in stock['code']: rs = bs.query_history_k_data_plus(s, 'date,code,close', start_date='2016-01-01', end_date='2019-12-31', adjustflag='2') while (rs.error_code == '0') & rs.next(): data_list.append(rs.get_row_data())df = pd.DataFrame(data_list, columns=rs.fields)df = df.apply(pd.to_numeric, errors='ignore')df['date']=pd.to_datetime(df['date'])bs.logout()df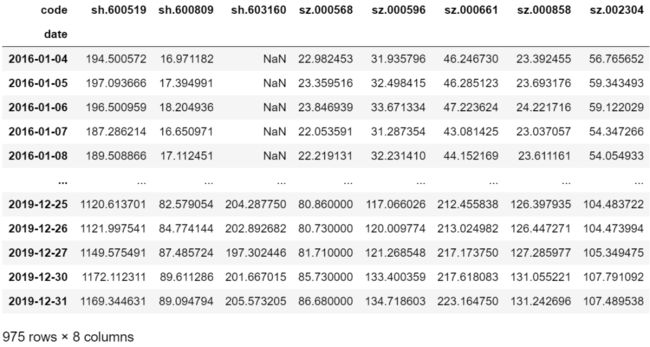
5.简单看一下股票历史价格图形
由于茅台实在过于一只独秀了,很难看出其他股票的涨幅和波动
df.plot(figsize=(15,10))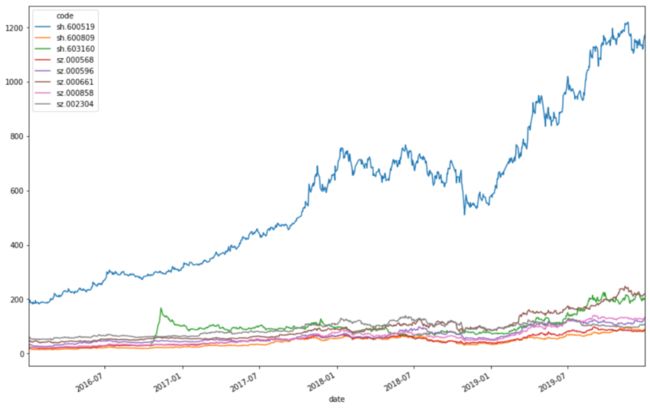
6. 把茅台剔除再看一下
df.drop('sh.600519', 1).plot(figsize=(15,10))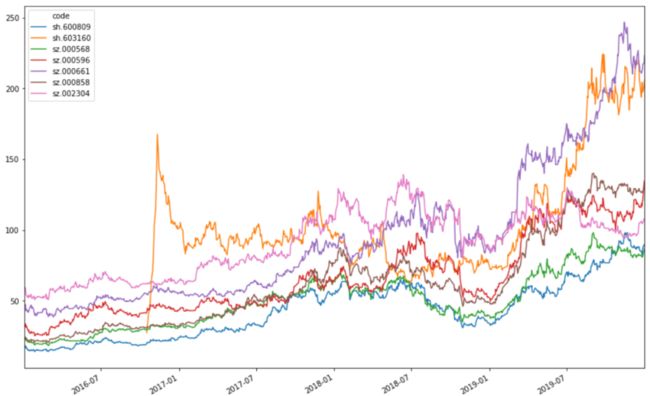
从这张图可以看出000661长春高新涨势和稳定性都很不错
那么假如我们有一定的资金,具体该怎么在这几只股票之间分配呢?
7. 计算最优股票组合
我们使用PyPortfolioOpt提供的模型,计算最优股票组合
# 1.计算期望报酬率和协方差mu = expected_returns.mean_historical_return(df)S = risk_models.sample_cov(df)# 2.夏普比率最大化的投资组合ef = EfficientFrontier(mu, S)weights = ef.max_sharpe()cleaded_weights = ef.clean_weights()ef.portfolio_performance(verbose=True)

模型返回的期望报酬率是58.6%,波动率27.2%,夏普比率2.08
建议的投资比例是600519茅台54.933%,603160汇顶科技28.82%,000661长春高新15.73%,000858五粮液0.51%。
验证投资组合模型
案例到上一步,已经给出了模型建议的投资组合。感兴趣的小伙伴可以继续验证一下PyPortfolioOpt的模型原理
1. 模型用股价变化代表每日收益率
returns = df.pct_change() # pct_change():当前元素与先前元素的相差百分比returns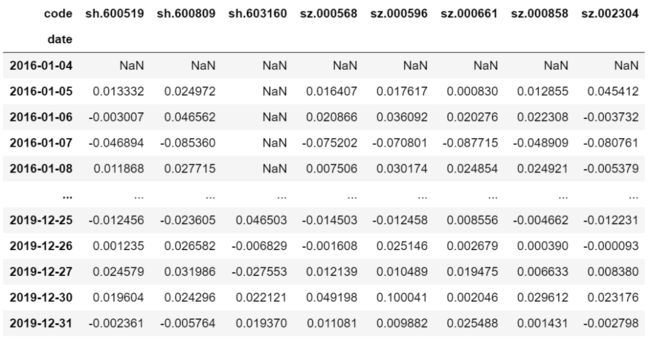
2. 计算期望收益
期望每日收益:Σ平均每日历史收益*股票权重
股票权重直接使用PyPortfolioOpt模型给出的最优股票组合权重进行验证
年化期望收益=期望每日收益*252(一年股市共252个交易日)
weights_value=np.array(list(weights.values())) #weights.values()的数据类型是OrderedDict:有序字典,操作可参考dictAnnualReturn = (returns.mean() * weights_value).sum()*252AnnualReturn0.5858831191150594
与上文比较第一个指标:(0.5858831191150594, 0.27212823050446977, 2.0794723063683196)
3. 模型用方差代表波动性
returns.cov()# cov():计算DataFrame系列之间的成对协方差。返回的数据是DataFrame的协方差矩阵。
4. 根据公式计算年化协方差和年化波动率
# 年化协方差AnnualVariance = np.dot(weights_value.T, np.dot(returns.cov()*252,weights_value))# 计算年化波动率:√协方差AnnualVolatility = np.sqrt(AnnualVariance)AnnualVolatility0.27212823050446977
与上文比较第二个指标:(0.5858831191150594, 0.27212823050446977, 2.0794723063683196)
5. 验证夏普比率
夏普比率是投资组合的收益减去每单位风险(波动率)的无风险利率。
![]()
下图:纵坐标是期望收益(AnnualisedReturns),横坐标是风险(AnnualiesdVolatility)

在模型中,我们设定了最优组合为max_sharpe(),也就是收益率最高的点。
SharpRatio=(AnnualReturn - 0.02)/AnnualVolatility #无风险报酬率模型默认2%SharpRatio2.0794723063683196
与上文比较第三个指标:(0.5858831191150594, 0.27212823050446977, 2.0794723063683196)
想了解更多课程,欢迎访问财码Python官网:www.fincode.com.cn
想进财码Python学习群的小伙伴可以添加财码小秘书~
往期课程推荐:
《财码Python量化选股(一)财经数据获取》
《财码Python量化选股(二)财经数据可视化》