LQBv22-Python：扩散

2020-/National_Java_B/B

小蓝在一张无限大的特殊画布上作画。
这张画布可以看成一个方格图，每个格子可以用一个二维的整数坐标表示。
小蓝在画布上首先点了一下几个点：(0, 0), (2020, 11), (11, 14), (2000, 2000)。
只有这几个格子上有黑色，其它位置都是白色的。
每过一分钟，黑色就会扩散一点。具体的，如果一个格子里面是黑色，它
就会扩散到上、下、左、右四个相邻的格子中，使得这四个格子也变成黑色
（如果原来就是黑色，则还是黑色）。
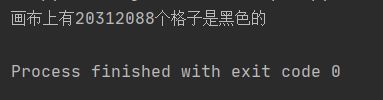
请问，经过 2020 分钟后，画布上有多少个格子是黑色的。

解题思路：
2020分钟也就是走了2020步，在这2020步内，如果平面上的某个点可以在2020步内走到已知的四个点的其中一个，那么这个点就是黑色的，也就是点与点之间的距离问题，根据曼哈顿距离公式，三层for循环，一层if判断，最后得到结果。
（但是超级慢…我运行了得有50s左右…hlja）
代码：

xy = [[0, 0], [2020, 11], [11, 14], [2000, 2000]]
count = 0
for i in range(-2020, 4041):
    for j in range(-2020, 4021):
        for k in range(0, 4):
            if (abs(i-xy[k][0]) + abs(j-xy[k][1])) <= 2020:
                count += 1
                break
print('画布上有{}个格子是黑色的'.format(count))

运行结果：