Dijkstra算法总结

Dijkstra算法总结

一、Dijkstra 算法的定义

老规矩先引用一下百度百科上关于 Dijkstra 算法的说明。

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

很显然，根据这段文字，我们可以了解到 Dijkstra 算法应用了贪心算法的思想，主要应用于有权图中最短路径问题。

二 、Dijkstra 算法的操作过程

因为这一算法的思路是从起始点开始，采用贪心算法的策略，每次遍历到离起始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。所以要实现这一想法，我们需要一个计算从起始点到各个顶点的最短路程的数组 dis [] 。

假设起始点为 start ，那么初始状态下，dis [ start ] = 0；

如果这个点的出度为零，将除起始点以外所有点的 dis [] 值赋为无穷大，这样便于在之后的遍历中如果找到路径，就能通过比较选取两者中较小的作为最短路程；

如果这个点的出度不为零，那么说明存在有向边由这个点指向其他点，假设终点为 end ，有向边为 （ start ，end ），边权（边的长度）为 w（ start ，end ），则 dis [ end ] = w（ start ，end ）；

重点！！！
若这个点的出度大于等于 2的时候，下次找离这个点最近的终点作为起始点，即寻找由这个点引出的边权最小的有向边来进行下一步操作。我们可以反推一下这样做的原因，假设这个点出度为二，由这个点引出的边权小的有向边为 A ，大的为 B ，如果我们选择了 B 的话，那么想要到 A ，最好的情况是只通过 B 这一个中转点，由 B 到 A，因为所有边的边权均为整数，到 B 的路程原本就大于 A，再加上由 B 到 A 的路程，就更不用说了。所以可以判断出从起始点直接到 A 一定是最短路径，所以将 A 作为下一次的起始点一定是正确的。

然后按照同样的思路重复上述操作，直到所有的点都被取完。

接下来我以下图为例，模拟一下整个过程。

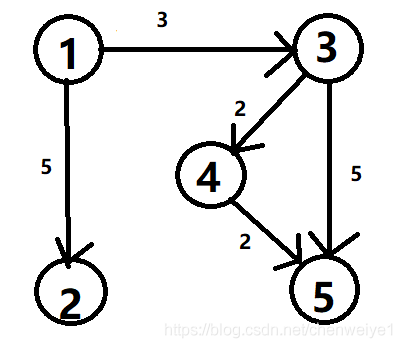
第一步：
一号可以通向二号和三号，所以把二号和三号赋上值。

第二步：
三号可以通向四号和五号，所以把四号和五号赋上值。

第三步：
因为 w（ 3 ，4 ）< w（ 3 ，5 ），所以选择四号，四号通向五号，1-3-4-5 这条路径上的权值之和为 7 ，7 < 8 ，所以用 7 来替换 8 。

总结一下，

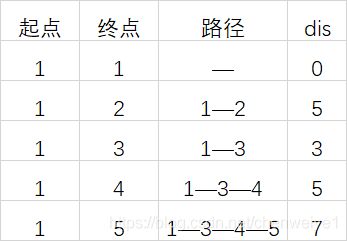
这就是最基本的 Dijkstra 算法的实现。

三、Dijkstra 算法例题应用

下面以单源最短路为例实际应用 Dijkstra 算法。

题目描述
给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入格式
第一行包含三个整数 n,m,s，n,m,s，分别表示点的个数、有向边的个数、出发点的编号。

接下来 m 行每行包含三个整数 u,v,w，u,v,w，表示一条 u→v 的，长度为 w 的边。

输出格式
输出一行 n 个整数，第 i 个表示 s 到第 i 个点的最短路径，若不能到达则输出 2^31-1。

输入输出样例
输入
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
输出
0 2 4 3

#include
using namespace std;
long long head[100005],to[200005],nxt[200005],len[200005],cnt,a[100005];
bool b[100005];
void cwy(int x,int y,int z){
     
	cnt++;
    to[cnt]=y;
    len[cnt]=z;
    nxt[cnt]=head[x];
    head[x]=cnt;
}//链式前向星；
priority_queue< pair<int,int> > q;//使用优先队列来维护 Dijkstra 算法；
int main(){
     
    int n,m,x,y,z,s;
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<=m;i++){
     
        scanf("%d%d%d",&x,&y,&z);
        cwy(x,y,z);
    }
    for(int i=1;i<=n;i++){
     
    	a[i]=0x7f;//正无穷大的赋值；
	}
    a[s]=0;//起始点本身赋零；
    q.push(make_pair(0,s));
    while(q.empty()==0){
     
        int x=q.top().second;
        q.pop(); 
        if(b[x]){
     
        	continue;
		}
        b[x]=1;
        for(int i=head[x];i;i=nxt[i]){
     
            int y=to[i],l=len[i];
            if(a[y]>a[x]+l){
     
                a[y]=a[x]+l;
                q.push(make_pair(-a[y],y));
            }
        }
    }
    for(int i=1;i<=n;i++){
     
    	printf("%d ",a[i]);
	}
    return 0;
} 

谢谢阅读！