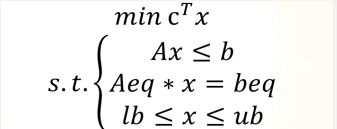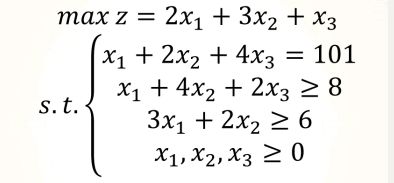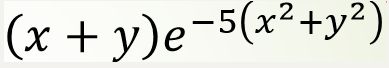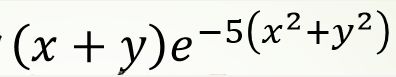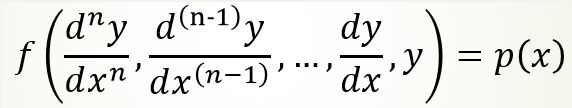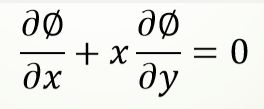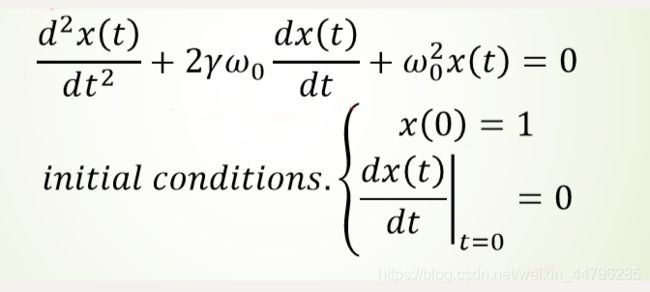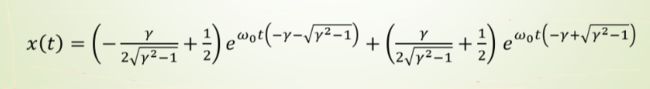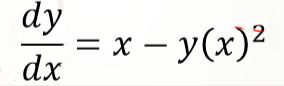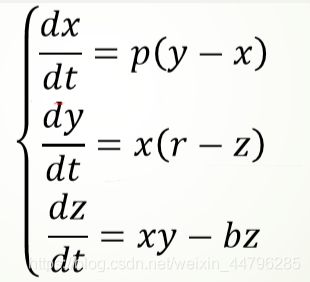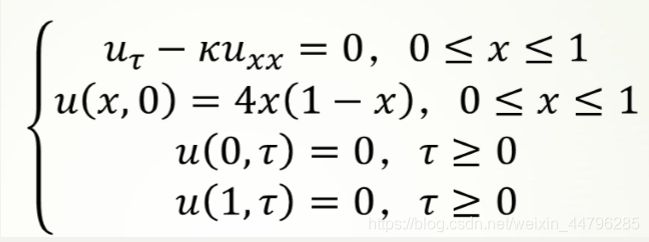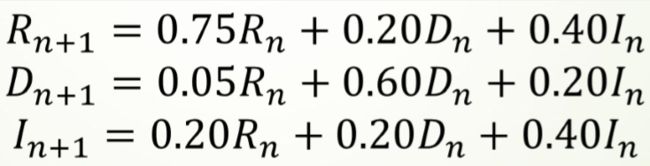数学建模问题的python相关代码
python之数模
本篇文章主要是python代码实例正文从线性规划开始
1. 环境搭建
数模中建议使用anaconda,自带相关库
1.1 使用anaconda
2. numpy库
3. pandas库
4. matplotlib库
5. 规划问题
5.1 线性规划
线性规划要求清晰两部分,目标函数和约束条件,求解前应转化为标准形式
from scipy import optimziae
import numpy as np
res = optimize.linprog(c,A,b,Aeq,beq,LB,UB,X0OPTIONS)
# 目标值函数最小值
res.fun
# 最优解
res.x
# 直接输出结果
res
以上是求最小值,如果求最大值则使c变为-c
- 易错
- 最大与最小的关系
- 不等式为小于等于,大于等于应转化为小于等于
- 注意A与Aeq的维度,一维为一列
import pulp as pp
# 目标函数的系数
z = [2,3,1]
# 约束
a = [[1,4,2],[3,2,0,]]
b = [8,6]
# 确定最大化/最小化问题 取决于sense的属性LpMaximize/LpMinimize
m = pp.LpProblem('问题描述(可选)',sense=pp.LpMinimize)
#定义三个变量放到列表中 lowBound为下边界
x = [pp.LpVariable(f'{i}', lowBound=0) for i in [1,2,3]]
# 定义目标函数,lpDot将两个列表位相乘再相加,添加到问题中
m += pp.lpDot(z,x)
# 问题添加约束条件
for i in range(len(a)):
m += (pp.lpDot(a[i],x) >= b[i])
# 求解
m.solve()
#输出结果
print(f'优化结果:{pp.value(m.objective)}')
print(f'参数取值:{pp.value(var) for var in x}')
代码
import pulp as pp
import numpy as np
from pprint import pprint
def transportation_problem(costs, x_max, y_max):
row = len(costs)
col = len(costs[0])
prob = pp.LpProblem('Transportation Problem', sense = pp.Lp
Maximixe)
var = [[pp.LpVariable(f'x{i}{j}',lowBound=0,cat=pp.LpInteger)for j in range (col) ] for i in range(row)]
# 将多维的数组变为1维的
flatten = lambda x:[y for li in x for y in flatten(li)] if type(x) is list else [x]
porb += pp.lpDot(flatten(var),costd.flatten())
for i in range(row):
prob += (pp.lpSum(var[i]) <= x_max[i])
for j in range(col):
prob += (pp.lpSum([var[i][j] for j in range(row)]) <= y_max[j])
prob.solve()
return {
'objective':pp.value(prob.objective),
'var':[[pp.value[i][j] for j in range(col)] for i in range(row)]
}
if __name__ == "__main__":
costs = np.array([[],[],[]])
x_max = []
y_max = []
res = transportation_problem(costs, x_max, y_max)
print(f'最大值为{res['objective']}')
print('各变量取值为:')
pprint(res['var'])
5.2 整数规划
与线性规划模型基本相同,额外的增加了部分变量为整数的的约束
分枝定界代码(最小值):
import math
from scipy.optimize import linprog
import sys
def integerPro(c, A, b, Aeq, beq, t=1.0E-12):
res = optimize.linprog(c, A_ub = A, b_ub=b, A_eq=Aeq, b_eq=beq)
if(type(res.x) if float):
bestX = [sys.maxsize]*len(c)
else:
bestX = res.x
baseVal = sum([x*y for x,y in zip(c,bestX)])
if all(( (x-math.floot(x))<t or (math.ceil(x)-x)<t )for x in bestX):
return (bestVal, bestX)
else:
ind = [i for i,x in enumerate(bestX) if (x-math,floor(x))>t and (math.ceil(x) - x)>t][0]
newCon1 = [0]*len(A[0])
newCon2 = [0]*len(A[0])
newCon1[ind] = -1
newCon2[ind] = 1
newA1 = A.copy()
newA2 = A.copy()
newA1.append(newCon1)
newA2.append(newCon2)
newB1 = b.copy()
newB2 = b.copy()
newB1.append(-math.ceil(best[ind]))
newB2.append(math.floor(best[ind]))
r1 = integerPro(c, newA1, newB1, Aeq, beq)
r2 = integerPro(c, newA2, newB2, Aeq, beq)
if r1[0] < r2[0]:
return r1
return r2
if __name__ == '__main__':
c = []
A = [[],[]]
b = []
Aeq = []
beq=[]
print(integerPro(c, A, b, Aeq, beq))
5.3 非线性规划
-
非线性规划可以分为两种
-
目标函数为凸函数
可以由很多常用库完成 -
目标函数为非凸函数
可以尝试以下方法
- 纯数学方法,求导数与极值
- 神经网络、深度学习(反向传播算法中链式求导过程)
- scipy.optimize.minimize()
-
程序样例:
计算1/x+x的最小值
from scipy.optimize import minimize
import numpy as np
# 定义非线性规划的函数,使用匿名函数的形式
def fun(args):
a = args
v = lambda x:a/x[0] +x[0]
return v
if __name__ == '__main__':
args = 1
x0 = np.asarray((2)) # 猜测初始值
res = minimize(fun(args),x0, method='SLSQP')
print(res.fun)
print(res.success)
print(res.x)
计算
( 2 + x 1 ) / ( 1 + x 2 ) − 3 x 1 + 4 x 3 (2 + x_1 )/ (1 + x_2) -3x_1 + 4x_3 (2+x1)/(1+x2)−3x1+4x3
的最小值,其中x1,x2,x3范围在0.1到0.9之间
from scipy.optimize import minimize
import numpy as np
def fun(args):
a,b,c,d = args
v = lambda x: (a+x[0])/(b+x[1]) - c*x[0] + d*x[2]
return v
# 定义约束条件
def con(args):
# 约束条件分为eq 和 ineq
# eq:函数结果等于0
# ineq:函数结果大于等于0
x1min,x1max,x2min,x2max,x3min,x3max = args
cons = ({
'type':'ineq','fun':lambda x:x[0]-x1min},
{
'type':'ineq','fun':lambda x:x[0]+x1max},
{
'type':'ineq','fun':lambda x:x[0]-x2min},
{
'type':'ineq','fun':lambda x:x[0]-x2max},
{
'type':'ineq','fun':lambda x:x[0]-x3min},
{
'type':'ineq','fun':lambda x:x[0]-x3max}
)
return cons
if __name__ == '__main__':
# 定义常量值
args = (2,1,3,4)
# 定义约束范围
args1 = (0.1,0.9,0.1,0.9,0.1,0.9)
cons = con(args1)
x0 = np.asarray((0.5,0.5,0.5))
res = minimize(fun(args),x0,method='SLSQP',constraints = cons)
print(res.fun)
print(res.success)
print(res.x)
- x0的设置影响最终结果:在初始值猜测值附近做局部最优解
6. 数值逼近问题
6.1 一维插值
插值函数经过样本点,拟合函数一般基于最小二乘法尽量靠近所有样本点穿过,常见插值方法:
- 拉格朗日插值法
- 分段插值法
- 样条插值法
程序样例1:
某电学元件的电压数据记录在0~2.25πA范围与电 流关系满足正弦函数,分别用线性插值和样条插值方法给 出经过数据点的数值逼近函数曲线。
import numpy as np
import pylab as pl
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 2*np.pi+np.pi/4, 10)
y = np.sin(x)
x_new = np.linspace(0, 2*np.pi+np.pi/4, 100)
f_linear = interpolate.interp1d(x, y)
tck = interpolate.splrep(x, y)
y_bspline = interpolate.splev(x_new, tck)
#可视化
plt.xlabel(u'安培/A')
plt.ylabel(u'伏特/V')
plt.plot(x, y, "o", label=u"原始数据")
plt.plot(x_new, f_linear(x_new), label=u"线性插值")
plt.plot(x_new, y_bspline, label=u"B-spline插值")
pl.legend()
pl.show()
高阶样条插值
样例2:
某电学元件的电压数据记录在0~10A范围与电流 关系满足正弦函数,分别用0-5阶样条插值方法给出经过 数据点的数值逼近函数曲线。
#创建数据点集
import numpy as np
x = np.linspace(0, 10, 11)
y = np.sin(x)
#绘制数据点集
import pylab as pl
pl.figure(figsize=(12,9))
pl.plot(x, y, 'ro')
#根据kind创建interp1d对象f、计算插值结果
xnew = np.linspace(0, 10, 101)
from scipy import interpolate
for kind in ['nearest', 'zero', 'linear', 'quadratic']:
f = interpolate.interp1d(x, y, kind = kind)
ynew = f(xnew)
pl.plot(xnew, ynew, label = str(kind))
pl.xticks(fontsize=20)
pl.yticks(fontsize=20)
pl.legend(loc='lower right’)
pl.show()
6.2 二维插值
样例3:
,完成图像 的二维插值使其变清晰。
import numpy as np
from scipy import interpolate
import pylab as pl
import matplotlib as mpl
def func(x, y):
return (x+y)*np.exp(-5.0*(x**2+y**2))
#X-Y轴分为15*15的网格
y, x = np.mgrid[-1:1:15j, -1:1:15j]
#计算每个网格点上函数值
fvals = func(x, y)
#三次样条二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')
#计算100*100网格上插值
xnew = np.linspace(-1,1,100)
ynew = np.linspace(-1,1,100)
fnew = newfunc(xnew, ynew)
#可视化
#让imshow的参数interpolation设置为’nearest’方便比较插值处理
pl.subplot(121)
im1 = pl.imshow(fvals, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im1)
pl.subplot(122)
im2 = pl.imshow(fnew, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im2)
pl.show()
二维插值的三维图
某图像表达式为
完成三维图像 的二维插值可视化。
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt
def func(x, y):
return (x+y)*np.exp(-5.0*(x**2+y**2))
#X-Y轴分为20*20的网格
x = np.linspace(-1,1,20)
y = np.linspace(-1,1,20)
x, y = np.meshgrid(x, y)
fvals = func(x, y)
#画分图1
fig = plt.figure(figsize=(9, 6))
ax = plt.subplot(1, 2, 1, projection = '3d')
surf = ax.plot_surface(x, y, fvals, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
plt.colorbar(surf, shrink=0.5, aspect=5)#添加颜色条标注
#二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')
#计算100*100网格上插值
xnew = np.linspace(-1,1,100)
ynew = np.linspace(-1,1,100)
fnew = newfunc(xnew, ynew)
xnew, ynew = np.meshgrid(xnew, ynew)
ax2 = plt.subplot(1, 2, 2, projection = '3d')
surf2 = ax.plot_surface(xnew, ynew, fnew, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('fnew(x,y)')
plt.colorbar(surf2, shrink=0.5, aspect=5)
#标注
plt.show()
6.3 OLS拟合
- 拟合指的是已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函 数中若干待定系数f(λ1, λ2,…,λn),使得该函数与已知点集的差别(最小 二乘意义)最小。
- 如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中), 否则叫作非线性拟合或者非线性回归。表达式也可以是分段函数,这 种情况下叫作样条拟合。
- 从几何意义上讲,拟合是给定了空间中的一些点,找到一个已知形式 未知参数的连续曲面来最大限度地逼近这些点;而插值是找到一个 ( 或几个分片光滑的)连续曲面来穿过这些点。
- 选择参数c使得拟合模型与实际观测值在曲线拟合各点的残差(或离 差)ek=yk-f(xk,c)的加权平方和达到最小,此时所求曲线称作在加权最 小二乘意义下对数据的拟合曲线,这种方法叫做最小二乘法。
对下列电学元件的电压电流记录结果进行最小二乘 拟合,绘制相应曲线。
电流(A)8.19 2.72 6.39 8.71 4.7 2.66 3.78
电压(V)7.01 2.78 6.47 6.71 4.1 4.23 4.05
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
plt.figure(figsize=(9,9))
X=np.array([8.19, 2.72, 6.39, 8.71, 4.7, 2.66, 3.78])
Y=np.array([7.01, 2.78, 6.47, 6.71, 4.1, 4.23, 4.05])
#计算以p为参数的直线与原始数据之间误差
def f(p):
k, b = p
return(Y-(k*X+b))
#leastsq使得f的输出数组的平方和最小,参数初始值为[1,0]
r = leastsq(f, [1,0])
k, b = r[0]
plt.scatter(X, Y, s=100, alpha=1.0, marker='o',label=u' 数据点')
x=np.linspace(0,10,1000)
y=k*x+b
ax = plt.gca()
ax.get_xlabel(…,fontsize=20)
ax.get_ylabel(…,fontsize=20)
plt.plot(x, y, color='r',linewidth=5, linestyle=":",markersize=20, label=u'拟合曲线')
plt.legend(loc=0, numpoints=1)
leg = plt.gca().get_legend()
ltext = leg.get_texts() plt.setp(ltext, fontsize='xx-large')
plt.xlabel(u'安培/A')
plt.ylabel(u'伏特/V')
plt.xlim(0, x.max() * 1.1)
plt.ylim(0, y.max() * 1.1)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(loc='upper left')
plt.show()
7. 微分方程问题
微分方程是用来描述某一类函数与其导数之间关系的方程, 其解是一个符合方程的函数。微分方程按自变量个数可分为 常微分方程 和 偏微分方程 ,前者表达通式
后者有两个以上的自变量,如:
7.1 微分方程的解析解
以求解阻尼谐振子的二阶ODE为例,其表达式为:
import numpy as np
from scipy import integrate
import sympy
def apply_ics(sol, ics, x, known_params):
free_params = sol.free_symbols – set(known_params)
eqs = [(sol.lhs.diff(x,n)sol.rhs.diff(x,n)).subs(x,0).subs(ics) for n in range(len(ics))]
sol_params = sympy.solve(eqs, free_params)
return sol.subs(sol_params)
sympy.init_printing()
#初始化打印环境
t, omega0, gamma = sympy.symbols(“t, omega_0, gamma”, positive=True)
#标记参数,且均为正
x = sympy.Function(‘x’)
# 标记x是微分函数,非变量
ode = x(t).diff(t,2)+2*gamma*omega0*x(t).diff(t)+omega0**2*x(t)
ode_sol = sympy.dsolve(ode)
# 用diff()和dsolve得到通解
ics = {
x(0): 1, x(t).diff(t).subs(t, 0): 0}
#将初始条件字典匹配
x_t_sol = apply_ics(ode_sol, ics, t, [omega0, gamma])
sympy.pprint(x_t_sol)
输出:
7.2 微分方程的数值解
场景图与数值解
当ODE无法求得解析解时,可以用scipy中的integrate.odeint求 数值解来探索其解的部分性质,并辅以可视化,能直观地展现 ODE解的函数表达。
以如下一阶非线性(因为函数y幂次为2)ODE为例:
现用odeint求其数值解:
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
import sympy
def plot_direction_field(x, y_x, f_xy, x_lim=(-5,5), ylim=(-5,5), ax=None):
f_np = sympy.lambdify((x, y_x), f_xy, ‘numpy’)
x_vec = np.linspace(x_lim[0], x_lim[1], 20)
y_vec = np.linspace(y_lim[0], y_lim[1], 20)
if ax is None:
_, ax = plt.subplots(figsize=(4,4))
dx = x_vec[1] – x_vec[0]
dy = y_vec[1] – y_vec[0]
for m, xx in enumerate(x_vec):
for n, yy in enumerate(y_vec):
Dy = f_np(xx, yy) * dx
Dx = 0.8*dx**2/np.sqrt(dx**2 + Dy**2)
Dy = 0.8*Dy*dy/np.sqrt(dx**2 + Dy**2)
ax.plot([xx-Dx/2, xx+Dx/2], [yy-Dy/2, yy+Dy/2], ‘b’, lw=0.5)
ax.axis(‘tight’)
ax.set_title(r”$%s$” %(sympy.latex(sympy.Eq(y_x.diff(x), f_xy))), fontsize=18)
return ax
x = sympy.symbols(‘x’)
y = sympy.Function(‘y’)
f = x-y(x)**2
f_np = sympy.lambdify((y(x),x),f)
#符号表达式转隐函数
y0 = 1 xp = np.linspace(0,5,100)
yp = integrate.odeint(f_np, y0, xp)
#初始y0解f_np,x范围xp
xn = np.linspace(0,-5,100)
yn = integrate.odeint(f_np, y0, xp)
fig, ax = plt.subplots(1,1,figsize=(4,4))
plot_direction_field(x, y(x), f, ax=ax)
#绘制f的场线图
ax.plot(xn, yn, ‘b’, lw=2)
ax.plot(xp, yp, ‘r’, lw=2)
plt.show()
洛伦兹曲线与数值解
以求解洛伦兹曲线为例,以下方程组代表曲线在xyz三个方向 上的速度,给定一个初始点,可以画出相应的洛伦兹曲线:
import numpy as np
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
def dmove(Point, t, sets):
p, r, b = sets
x, y, z = Point
return np.array([p*(y-x), x*(r-z), x*y-b*z])
t = np.arange(0, 30, 0.001)
P1 = odeint(dmove, (0., 1., 0.), t, args=([10., 28., 3.],))
P2 = odeint(dmove, (0., 1.01, 0.), t, args=([10., 28., 3.],))
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(P1[:,0], P1[:,1], P1[:,2])
ax.plot(P2[:,0], P2[:,1], P2[:,2])
plt.show()
7.3 传染病模型
SI、SIS、SIR、SIRS、SEIR、 SEIRS共六个模型
-
SI
import numpy as np import scipy.integrate as spi import matplotlib.pyplot as plt N = 10000 # N为人群总数 beta = 0.25 # β为传染率系数 gamma = 0 # gamma为恢复率系数 I_0 = 1 # I_0为感染者的初始人数 S_0 = N- I_0 # S_0为易感染者的初始人数 T = 150 # T为传播时间 INI = (S_0, I_0) # INI为初始状态下的数组 def funcSI(inivalue,_): Y = np.zeros(2) X = inivalue Y[0] = -(beta*X[0]*X[1])/N+gamma*X[1] # 易感个体变化 Y[1] = (beta*X[0]*X[1])/N-gamma*X[1] # 感染个体变化 return Y T_range = np.arrange(0, T+1) RES = spi.odeint(funcSI, INI, T_range) plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.') plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.') plt.title('SI Model') plt.legend() plt.xlabel('Day') plt.ylabel('Number') plt.show() -
SIS-Model
import numpy as np import scipy.integrate as spi import matplotlib.pyplot as plt N = 10000 # N为人群总数 beta = 0.25 # β为传染率系数 gamma = 0.05 # gamma为恢复率系数 I_0 = 1 # I_0为感染者的初始人数 S_0 = N- I_0 # S_0为易感染者的初始人数 T = 150 # T为传播时间 INI = (S_0, I_0) # INI为初始状态下的数组 def funcSIS(inivalue,_): Y = np.zeros(2) X = inivalue Y[0] = -(beta*X[0])/N*X[1]+gamma*X[1] # 易感个体变化 Y[1] = (beta*X[0]*X[1])/N-gamma*X[1] # 感染个体变化 return Y T_range = np.arrange(0, T+1) RES = spi.odeint(funcSIS, INI, T_range) plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.') plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.') plt.title('SIS Model') plt.legend() plt.xlabel('Day') plt.ylabel('Number') plt.show() -
SIR-Model
import numpy as np import scipy.integrate as spi import matplotlib.pyplot as plt N = 10000 # N为人群总数 beta = 0.25 # β为传染率系数 gamma = 0.05 # gamma为恢复率系数 I_0 = 1 # I_0为感染者的初始人数 R_0 = 0 # R_0为治愈者的初始人数 S_0 = N - I_0 – R_0 # S_0为易感染者的初始人数 T = 150 # T为传播时间 INI = (S_0, I_0, R_0) # INI为初始状态下的数组 def funcSIR(inivalue,_): Y = np.zeros(3) X = inivalue Y[0] = -(beta*X[0] *X[1])/N #易感个体变化 Y[1] = (beta*X[0]*X[1])/N-gamma*X[1]#感染个体变化 Y[2] = gamma*X[1] #治愈个体变化 return Y T_range = np.arrange(0, T+1) RES = spi.odeint(funcSIR, INI, T_range) plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.') plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.') plt.plot(RES[:,2],color = 'green',label = 'Recovery',marker = '.') plt.title('SIR Model') plt.legend() plt.xlabel('Day') plt.ylabel('Number') plt.show() -
SIRS-Model
import numpy as np import scipy.integrate as spi import matplotlib.pyplot as plt N = 10000 # N为人群总数 beta = 0.25 # β为传染率系数 gamma = 0.05 # gamma为恢复率系数 Ts = 7 # Ts为抗体持续时间 I_0 = 1 # I_0为感染者的初始人数 R_0 = 0 # R_0为治愈者的初始人数 S_0 = N - I_0 – R_0 # S_0为易感染者的初始人数 T = 150 # T为传播时间 INI = (S_0, I_0, R_0) # INI为初始状态下的数组 def funcSIRS(inivalue,_): Y = np.zeros(3) X = inivalue Y[0] = -(beta*X[0]*X[1])/N+X[2]/Ts #易感个体变化 Y[1] = (beta*X[0]*X[1])/N-gamma*X[1]#感染个体变化 Y[2] = gamma*X[1]-X[2]/Ts #治愈个体变化 return Y T_range = np.arrange(0, T+1) RES = spi.odeint(funcSIRS, INI, T_range) plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.') plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.') plt.plot(RES[:,2],color = 'green',label = 'Recovery',marker = '.') plt.title('SIRS Model') plt.legend() plt.xlabel('Day') plt.ylabel('Number') plt.show() -
SIER-Model
import numpy as np import scipy.integrate as spi import matplotlib.pyplot as plt N = 10000 # N为人群总数 beta = 0.25 # β为传染率系数 gamma = 0.05 # gamma为恢复率系数 Te = 14 # Te为疾病潜伏期 I_0 = 1 # I_0为感染者的初始人数 E_0 = 0 # E_0为潜伏者的初始人数 R_0 = 0 # R_0为治愈者的初始人数 S_0 = N - I_0 – R_0 – E_0 # S_0为易感染者的初始人数 T = 150 # T为传播时间 INI = (S_0, E_0, I_0, R_0) # INI为初始状态下的数组 def funcSEIR(inivalue,_): Y = np.zeros(4) X = inivalue Y[0] = -(beta*X[0]*X[2])/N #易感个体变化 Y[1] = (beta*X[0]*X[2]/N-X[1]/Te) # 潜伏个体变化 Y[2] = X[1]/Te-gamma*X[2]#感染个体变化 Y[3] = gamma*X[2] #治愈个体变化 return Y T_range = np.arrange(0, T+1) RES = spi.odeint(funcSEIR, INI, T_range) plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.') plt.plot(RES[:,1],color = 'orange',label = 'Exposed',marker = '.') plt.plot(RES[:,2],color = 'red',label = 'Infection',marker = '.') plt.plot(RES[:,3],color = 'green',label = 'Recovery',marker = '.') plt.title('SETR Model') plt.legend() plt.xlabel('Day') plt.ylabel('Number') plt.show() -
SIERS-Model
import numpy as np import scipy.integrate as spi import matplotlib.pyplot as plt N = 10000 # N为人群总数 beta = 0.25 # β为传染率系数 gamma = 0.05 # gamma为恢复率系数 Ts = 7 # Ts为抗体持续时间 Te = 14 # Te为疾病潜伏期 I_0 = 1 # I_0为感染者的初始人数 E_0 = 0 # E_0为潜伏者的初始人数 R_0 = 0 # R_0为治愈者的初始人数 S_0 = N - I_0 – R_0 – E_0 # S_0为易感染者的初始人数 T = 150 # T为传播时间 INI = (S_0, E_0, I_0, R_0) # INI为初始状态下的数组 def funcSEIRS(inivalue,_): Y = np.zeros(4) X = inivalue Y[0] = -(beta*X[0]*X[2])/N+X[3]/Ts #易感个体变化 Y[1] = (beta*X[0]*X[2]/N-X[1]/Te) # 潜伏个体变化 Y[2] = X[1]/Te-gamma*X[2]#感染个体变化 Y[3] = gamma*X[2]-X[3]/Ts #治愈个体变化 return Y T_range = np.arrange(0, T+1) RES = spi.odeint(funcSEIRS, INI, T_range) plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.') plt.plot(RES[:,1],color = 'orange',label = 'Exposed',marker = '.') plt.plot(RES[:,2],color = 'red',label = 'Infection',marker = '.') plt.plot(RES[:,3],color = 'green',label = 'Recovery',marker = '.') plt.title('SETRS Model') plt.legend() plt.xlabel('Day') plt.ylabel('Number') plt.show()
8. 图论
8.1 Dijkstra
Dijkstra算法能求一个顶点到另一顶点最短路径。
-
样例1
如下图所示,我们需要从①点走到⑨点,每条边的红色数 字代表这条边的长度,我们如何找到①到⑨的最短路径呢?

from collections import defaultdict from heapq import * inf = 99999 # 不连通值 mtx_graph = [[0, 1, inf, 3, inf, inf, inf, inf, inf], [1, 0, 5, inf, 2, inf, inf, inf, inf], [inf, inf, 0, 1, inf, 6, inf, inf, inf], [inf, inf, inf, 0, inf, 7, inf, 9, inf], [inf, 2, 3, inf, 0, 4, 2, inf, 8], [inf, inf, 6, 7, inf, 0, inf, 2, inf], [inf, inf, inf, inf, inf, 1, 0, inf, 3], [inf, inf, inf, inf, inf, inf, 1, 0, 2], [inf, inf, inf, inf, 8, inf, 3, 2, 0]] m_n = len(mtx_graph)#带权连接矩阵的阶数 edges = [] #保存连通的两个点之间的距离(点A、点B、距离) for i in range(m_n): for j in range(m_n): if i!=j and mtx_graph[i][j]!=inf: edges.append(i,j,mtx_graph[i][j]) def dijkstra(edges, from_node, to_node): go_path = [] to_node = to_node-1 g = defaultdict(list) for l,r,c in edges: g[l].append((c,r)) q, seen = [(0, from_node-1, ())], set() while q: (cost, v1, path) = heappop(q)#堆弹出当前路径最小成本 if v1 not in seen: seen.add(v1) path = (v1, path) if v1 == to_node: break for c, v2 in g.get(v1, ()): if v2 not in seen: heappush(q, (cost+c, v2, path)) if v1!=to_node: #无法到达 return float[‘inf’], [] if len(path)>0: left=path[0] go_path.append(left) right=path[1] while len(right)>0: left=right[0] go_path.append(left) right=right[1] go_path.reverse() #逆序变换 for i in range(len(go_path)): #标号加1 go_path[i]=go_path[i]+1 return cost, go_path leght, path = Dijkstra(edges, 1, 9) print(‘最短距离为:’+str(leght)) print(‘前进路径为:’+str(path))
8.2 Floyd
Floyd 通过动态规划解决任意两点间的最短路径(多源最短路径)的问题,可以正确处理负权的最短路径问题
同样例1:
from collections import defaultdict
from heapq import *
inf = 99999 # 不连通值
mtx_graph = [[0, 1, inf, 3, inf, inf, inf, inf, inf],
[1, 0, 5, inf, 2, inf, inf, inf, inf],
[inf, inf, 0, 1, inf, 6, inf, inf, inf],
[inf, inf, inf, 0, inf, 7, inf, 9, inf],
[inf, 2, 3, inf, 0, 4, 2, inf, 8],
[inf, inf, 6, 7, inf, 0, inf, 2, inf],
[inf, inf, inf, inf, inf, 1, 0, inf, 3],
[inf, inf, inf, inf, inf, inf, 1, 0, 2],
[inf, inf, inf, inf, 8, inf, 3, 2, 0]]
def Floyd(graph):
N=len(graph)
A=np.array(graph)
path=np.zeros((N,N))
for i in range(0,N):
for j in range(0,N):
if A[i][j]!=inf:
path[i][j]=j
for k in range(0,N):
for i range(0,N):
for j in range(0,N):
if A[i][j]+A[k][j]<A[i][j]:
A[i][j]=A[i][k]+A[k][j]
path[i][j]=path[i][k]
for i in range(0,N):
for j in range(0,N):
path[i][j]=path[i][j]+1
print(‘距离 = ’)
print(A)
print(‘路径 = ’)
print(path)
Floyd(mtx_graph)
8.3 机场航线设计
- 起始点和目的地可以作为节点,其他信息应当作为节点 或边属性;单条边可以被认为是一段旅程。这样的旅程 将有不同的时间,航班号,飞机尾号等相关信息。
- 注意到年,月,日和时间信息分散在许多列;想创建一 个包含所有这些信息的日期时间列,还需要将预计的 (scheduled)和实际的(actual)到达离开时间分开;最终 应该有4个日期时间列(预计到达时间、预计起飞时间、 实际到达时间和实际起飞时间)
- 时间格式问题
- 数据类型问题
- NaN值的麻烦
**数据导入、观察变量 **
import numpy as np
import pandas as pd
data = pd.read_csv(‘data/Airlines.csv’)
data.shape
>(100, 16)
data.dtypes
>year int64
>month int64
>day int64
>dep_time float64
>sched_dep_time int64
>dep_delay float64
>arr_time float64
>sched_arr_time int64
>arr_delay float64
**数据清洗 **
#将sched_dep_time转换为'std'—预定的出发时间
data['std'] = data.sched_dep_time.astype(str).str.replace('(\d{2}$)', '') + ':' + data.sched_dep_time.astype(str).str.extract('(\d{2}$)', expand=False) + ':00’
#将sched_arr_time转换为“sta”—预定到达时间
data['sta'] = data.sched_arr_time.astype(str).str.replace('(\d{2}$)', '') + ':' + data.sched_arr_time.astype(str).str.extract('(\d{2}$)', expand=False) + ':00’
#将dep_time转换为'atd' -实际出发时间
data['atd'] = data.dep_time.fillna(0).astype(np.int64).astype(str).str.replace('(\d{2}$)', '') + ':' + data.dep_time.fillna(0).astype(np.int64).astype(str).str.extract('(\d{2}$)', expand=False) + ':00’
#将arr_time转换为'ata' -实际到达时间
data['ata'] = data.arr_time.fillna(0).astype(np.int64).astype(str).str.replace('(\d{2}$)', '') + ':' + data.arr_time.fillna(0).astype(np.int64).astype(str).str.extract('(\d{2}$)',
时间信息合并
data['date'] = pd.to_datetime(data[['year', 'month', 'day']])
data = data.drop(columns = ['year', 'month', 'day'])
**创建图 **
import networkx as nx
FG = nx.from_pandas_edgelist(data, source='origin', target='dest', edge_attr=True,) FG.nodes()
# 查看所有节点
FG.edges()
# 查看所有边
nx.draw_networkx(FG, with_labels=True) #快速查看图表,发现3个十分繁忙的机场
nx.algorithms.degree_centrality(FG)#100条记录3机场
nx.density(FG) # 图的平均边密度 0.09047619047619047
nx.average_shortest_path_length(FG) #图中所有路径的平均最短路径长度2.36984126984127
nx.average_degree_connectivity(FG)
#对于一个度为k的节点-它的邻居度的平均值是多少? #{1: 19.307692307692307, 2: 19.0625, 3: 19.0, 17: 2.0588235294117645, 20: 1.95}
计算航线:
# 以JAX和DFW机场为例,先按照求取距离最短的路径
for path in nx.all_simple_paths(FG, source='JAX', target='DFW'):
print(path)
dijpath = nx.dijkstra_path(FG, source='JAX', target='DFW')
dijpath
# 输出: ['JAX', 'JFK', 'SEA', 'EWR', 'DFW’]
# 再按照求取飞行时间最短的路径
shortpath = nx.dijkstra_path(FG, source='JAX', target='DFW', weight='air_time')
shortpath
# 输出: ['JAX', 'JFK', 'BOS', 'EWR', 'DFW']
9. 回归模型
9.1 多元回归
-
选取数据
import pandas as pd import seaborn as sns import matplotlib.pyplot as plt import matplotlib as mpl #显示中文 def mul_lr(): pd_data=pd.read_excel('C:\\Users\\lenovo\\Desktop\\test.xlsx') mpl.rcParams['font.sans-serif'] = ['SimHei'] #配置显示中文,否则乱码 mpl.rcParams['axes.unicode_minus']=False #用来正常显示负号 sns.pairplot(pd_data, x_vars=['中证500','泸深300','上证50','上证180'], y_vars=' 上证指数',kind="reg", size=5, aspect=0.7) plt.show() -
构建训练集与测试集,并构建模型
from sklearn.model_selection import train_test_split #这里是引用了交叉验证 from sklearn.linear_model import LinearRegression #线性回归 from sklearn import metrics import numpy as np def mul_lr(): #剔除日期数据 X=pd_data.loc[:,('中证500','泸深300','上证50','上证180')] y=pd_data.loc[:,'上证指数'] X_train,X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=100) linreg = LinearRegression() model=linreg.fit(X_train, y_train) print (model) # 训练后模型截距 print (linreg.intercept_) # 训练后模型权重(特征个数无变化) print (linreg.coef_) -
模型预测
y_pred = linreg.predict(X_test) print (y_pred) #10个变量的预测结果 -
模型评估
sum_mean=0 for i in range(len(y_pred)): sum_mean+=(y_pred[i]-y_test.values[i])**2 sum_erro=np.sqrt(sum_mean/10) #这个10是你测试级的数量 # RMSE print ("RMSE:",sum_erro) #做预测对比曲线 plt.figure() plt.plot(range(len(y_pred)),y_pred,'b',label="predict") plt.plot(range(len(y_pred)),y_test,'r',label="test") plt.legend(loc="upper right") #显示图中的标签 plt.xlabel("the number of sales") plt.ylabel('value of sales') plt.show()
9.2 logistic回 归
鸢尾花数据集的logistic回 归
-
鸢尾花数据集
鸢尾花有三个亚属,分别是山鸢尾(Iris-setosa)、变色鸢尾(Irisversicolor)和维吉尼亚鸢尾(Iris-virginica)。该数据集一共包含4个特 征变量,1个类别变量。共有150个样本,iris是鸢尾植物,这里存储了其萼片 和花瓣的长宽,共4个属性,鸢尾植物分三类。
-
绘制散点图
import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import load_iris iris = load_iris() #获取花卉两列数据集 DD = iris.data X = [x[0] for x in DD] Y = [x[1] for x in DD] plt.scatter(X[:50], Y[:50], color='red', marker='o', label='setosa') plt.scatter(X[50:100], Y[50:100], color='blue', marker='x', label='versicolor') plt.scatter(X[100:], Y[100:],color='green', marker='+', label='Virginica') plt.legend(loc=2) #左上角 plt.show() -
逻辑回归分析
from sklearn.linear_model import LogisticRegression iris = load_iris() X = iris.data[:, :2] #获取花卉两列数据集 Y = iris.target lr = LogisticRegression(C=1e5) lr.fit(X,Y) #meshgrid函数生成两个网格矩阵 h = .02 x_min, x_max = X[:, 0].min()-.5, X[:, 0].max()+.5 y_min, y_max = X[:, 1].min()-.5, X[:, 1].max()+.5 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = lr.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.figure(1, figsize=(8,6)) plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired) plt.scatter(X[:50,0], X[:50,1], color='red',marker='o', label='setosa') plt.scatter(X[50:100,0], X[50:100,1], color='blue', marker='x', label='versicolor') plt.scatter(X[100:,0], X[100:,1], color='green', marker='s', label='Virginica') plt.xlabel('Sepal length') plt.ylabel('Sepal width') plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.xticks(()) plt.yticks(()) plt.legend(loc=2) plt.show()
10. 差分方程问题
10.1 递推关系
差分方程建模的关键在于如何得到第n组数据与第n+1组数据之间 的关系。
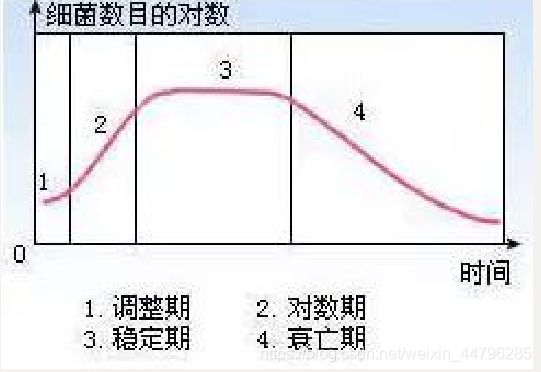
递推关系-酵母菌生长模型 :
如图所示我们用培养基培养细菌时, 其数量变化通常会经历这四个时期。 这个模型针对前三个时期 建一个大致的模型: 调整期、对数期、稳定期。
-
已有数据绘图
import matplotlib.pyplot as plt time = [i for i in range(0,19)] number = [9.6,18.3,29,47.2,71.1,119.1,174.6,257.3, 350.7,441.0,513.3,559.7,594.8,629.4,640.8, 651.1,655.9,659.6,661.8] plt.title('Relationship between time and number')#创建标题 plt.xlabel('time')#X轴标签 plt.ylabel('number')#Y轴标签 plt.plot(time,number)#画图 plt.show()#显示 -
分析:
酵母菌数量增长有一个这样的规律:当某些资源只能支撑某个最大限度的种群
数量,而不能支持种群数量的无限增长,当接近这个最大值时,种群数量的增
长速度就会慢下来。- 两个观测点的值差△p来表征增长速度‘
- △p与目前的种群数量有关,数量越大,增长速度越快
- △p还与剩余的未分配的资源量有关,资源越多,增长速度越快
- 然后以极限总群数量与现有种群数量的差值表征剩余资源量
模型:
△ p = P n + 1 一 P n = k ( 665 − P n ) P n △p=P_{n+1}一P_n=k(665 - P_n)P_n △p=Pn+1一Pn=k(665−Pn)Pn -
计算模型表达式
import numpy as np pn = [9.6,18.3,29,47.2, 71.1,119.1, 174.6, 257.3, 350.7, 441.0, 513.3, 559.7, 594.8, 629.4, 640.8, 651.1, 655.9, 659.6] deltap = [8.7, 10.7.18.2,23.9, 48,55.5, 82.7, 93.4, 90.3, 72.3, 46.4,35.1, 34.6, 11.4, 10.3,4.8,3.7,2.2] gn = np. array (pn) factor = pn* (665-pn) f = np.polyfit (factor, deltap, 1) print (f) -
绘制预测曲线
import matplotlib.pyplot as plt p0 = 9.6 p_list = [] for i in range(20): p_list.append(p0) p0 = 0.00081448*(665-p0)*p0+p0 plt.plot(p_list) plt.show()
10.2 显式差分
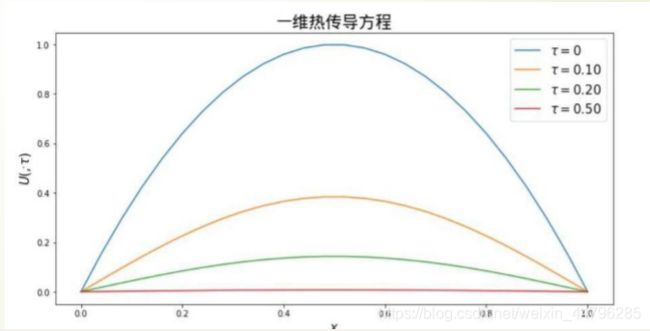
显式差分-热传导方程
k为热传导系数,第二式是初始条件低三四式是边值条件,热传导方程如下:
-
初始条件形状
from matplotlib import pylab import seaborn as sns import numpy as np from CAL.PyCAL import * font.set_size(20) def initialCondition(x): return 4.0*(1.0-x)*x xArray = np.linspace(0,1.0,50) yArray = map(initialCondition, xArray) pylab.figure(figsize=(12,6)) pylab.xlabel(‘$x$’,fontsize=15) pylab.ylabel(‘$f(x)$’,fontsize=15) pylab.title(u’一维热传导方程初值条 件’,fontproperties=font)
定义基本变量:
- N 空间方向的网格数
- M 时间方向的网格数
- T 最大时间期限
- X 最大空间范围
- U 用来存储差分网格点值的矩阵
N = 25
M = 2500
T = 1.0
X = 1.0
xArray = np.linspace(0,1.0,50)
yArray = map(initialCondition, xArray)
starValues = yArray
U = np.zeros((N+1,M+1))
U[:,0]=starValues
dx=X/N
dt=T/N
kappa=1.0
rho=kappa*dt/dx/dx
for k in range(0,N):
for j in range(1,N):
U[j][k+1]=rho*U[j-1][k]+ (1.-2*rho)*U[j][k]+ rho*U[j+1][k]
U[0][k+1]=0.
U[N][k+1]=0.
pylab.figure(figsize=(12,6))
pylab.plot(xArray, U[:,0])
pylab.plot(xArray, U[:,int(0.10/dt)])
pylab.plot(xArray, U[:,int(0.20/dt)])
pylab.plot(xArray, U[:,int(0.50/dt)])
pylab.xlabel(‘$x$’, fontsize=15)
pylab.ylabel(r‘$U(\dot,\tau)$’,fontsize=15)
pylab.title(u’一维热传导方程’,fontproperties=font)
pylab.legend([r’$\tau=0.$’, r’$\tau=0.10$’, r’$\tau=0.20$’, r’$\tau=0.50$’],fontsize=15)
输出:
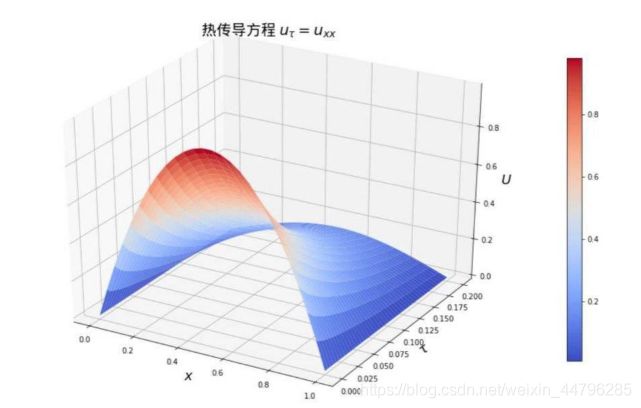
三维立体图查看整体热传导过程 :
tArray = np.linspace(0, 0.2, int(0.2/dt)+1)
xGride, tGride = np.meshgrid(xArray, tArray)
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = pylab.figure(figsize=(16,10))
ax = fig.add_subplot(1,1,1,projection=‘3d’)
surface = ax.plot_surface(xGride, tGride, U[:,:int(0.2/dt)+1].T, cmap=cm.coolwarm)
ax.set_xlabel(“$x$”, fontdict={
“size”:18})
ax.set_ylabel(r“$\tau$”, fontdict={
“size”:18})
ax.set_zlabel(r”$U$”, fontdict={
“size”:18})
ax.set_title(u”热传导方程 $u_\\tau = u_{
xx}$”, fontproperties=font)
fig.colorbar(surface, shrink=0.75)
输出:
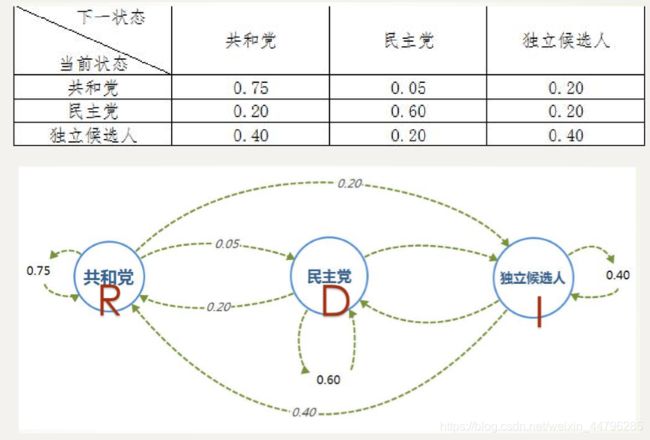
10.3 马尔科夫链
马尔科夫链是由具有以下性质的一系列事件构成的过程:
- 一个事件有有限多个结果,称为状态,该过程总是这些状态中的一个;
- 在过程的每个阶段或者时段,一个特定的结果可以从它现在的状态转移到任 何状态,或者保持原状;
- 每个阶段从一个状态转移到其他状态的概率用一个转移矩阵表示,矩阵每行 的各元素在0到1之间,每行的和为1。
实例:选举投票预测
以美国大选为例,首先取得过去十次选举的历史数据,然后根据历史数据得到 选民意向的转移矩阵。
构建差分方程组
通过求解差分方程组,推测出选民投票意向趋势
import matplotlib.pyplot as plt
RLIST = [0.33333]
DLIST = [0.33333]
ILIST = [0.33333]
for i in range(40):
R = RLIST[i]*0.75+DLIST[i]*0.20+ILIST[i]*0.40
RLIST.append(R)
D = RLIST[i]*0.05+DLIST[i]*0.60+ILIST[i]*0.20
DLIST.append(D)
I = RLIST[i]*0.20+DLIST[i]*0.20+ILIST[i]*0.40
ILIST.append(I)
plt.plot(RLIST)
plt.plot(DLIST)
plt.plot(ILIST)
plt.xlabel('Time')
plt.ylabel('Voting percent')
plt.annotate('DemocraticParty',xy = (5,0.2))
plt.annotate('RepublicanParty',xy = (5,0.5))
plt.annotate('IndependentCandidate',xy = (5,0.25))
plt.show()
print(RLIST,DLIST,ILIST)