《深度学习入门：基于Python的理论与实现》学习笔记 系列之一

笔记汇总

（此笔记是基于《深度学习入门》这本书的重点知识汇总。）
第一周任务主要了解了：

• 感知机/多层感知机MLP
• NumPy多维数组的运算
• 正向传播（正向传播算法，也叫前向传播算法）
• 激活函数
• 损失函数

1、感知机/多层感知机（MLP）

感知机是什么？

多个输入，一个输出。改变权重w可以实现与、与非和或门。(构造相同，只是权重参数不一样)

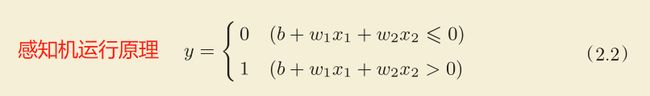
图1-1 感知机原理（用的激活函数是阶跃函数）

1、用感知机原理实现一个与门

def AND(x1,x2):  
    x = np.array([0,1])
    w = np.array([0.5,0.5])
    b = -0.7
    tmp = x*w + b
    if tmp > 0:
        return 1
    elif tmp <= 0:
        return 0

2、用 -b 代替 θ，用NumPy实现感知机

>>> import numpy as np
>>> x = np.array([0, 1])     # 输入
>>> w = np.array([0.5, 0.5]) # 权重
>>> b = -0.7                 # 偏置
>>> w*x
array([ 0. ,  0.5])
>>> np.sum(w*x)
0.5
>>> np.sum(w*x) + b
-0.19999999999999996   # 大约为-0.2（由浮点小数造成的运算误差）

单层感知机的缺点：

• 不能实现异或门（因为没有这样的w和b参数存在）
• 为什么不能实现 ？
  • 单层感知机只能表示由一条直线分割的空间，这种空间为线性空间；而异或是非线性的，空间不能由直线分割，不过可由曲线分割，这种空间为非线性空间

如何改进：叠加层。

• 引出多层感知机（MLP）

其实异或门可由 与、与非、或门 组合而成。所以异或是多层结构的神经网络（两层）。（一层不行，咱就叠加层）（一顿火锅解决不了，咱就再来一顿！）

而且两层感知机运作过程好比流水线作业，一层层传递

总结：单层感知机（线性）通过叠加层可进行非线性的表示

• 单层感知机——表示线性空间
• 多层感知机——表示非线性空间，理论上还可表示计算机

多层感知机 = 神经网络

感知机与神经网络的区别：激活函数不同！

• 单层感知机：激活函数为阶跃函数
• 神经网络：激活函数不是阶跃函数

2、NumPy多维数组的运算部分总结

np.ndim(A) ：获取数组的维数，维数由最小的行或者列来确定

A.shape ：获取数组的形状（几行几列），返回元组（tuple）

A.shape[0] 代表第一个维度，即行；
A.shape[1] 代表第二个维度，即列

二维数组 = 矩阵
比如：
A = [[1,2],
[3,4],
[5,6]]

行 = 第一个维度（第0维） = A.shape[0] = 有三个元素（有三行）
列 = 第二个维度（第1维） = A.shape[1] = 有两个元素（有两列）

np.dot()：矩阵乘法
接收两个NumPy数组作为参数，并返回数组的乘积。

3、前向传播（forward propagation）

前向传播的实现（即假设已经知道了参数的值，进行分类任务）
= 假设我们已经学习到了参数，进行推理任务，也就是对输入数据进行分类，这就是前向传播的过程。
即 前向传播 = 此处的推理处理

三层前向传播的神经网络的实现

# 三层前向传播的神经网络的实现
import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))   

# 初始化神经网络，给w,b具体值，用字典存储起来
def init_network():
    network = {
     }
    network['w1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
    network['b1'] = np.array([0.1,0.2,0.3])
    network['w2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
    network['b2'] = np.array([0.1,0.2])
    network['w3'] = np.array([[0.1,0.3],[0.2,0.4]])
    network['b3'] = np.array([0.1,0.2])
    return network

# 前向传播算法,输入x,w,b;加激活函数sigmoid,输出y
# 将输入信号转化为输出信号的处理过程
def forward(network,x):
    w1,w2,w3 = network['w1'], network['w2'], network['w3']
    b1,b2,b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x,w1) + b1
    z1 = sigmoid(a1)
    
    a2 = np.dot(z1,w2) + b2
    z2 = sigmoid(a2)
    
    a3 = np.dot(z2,w3) + b3
    y = a3
    
    return y

# 1、调用init_network()初始化神经网络的w,b; 
# 2、给x具体值; 
# 3、调用forward前向传播算法，输出y
network = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
print(y)

[ 0.31682708  0.69627909]

4、激活函数

《深度学习入门》：一般而言，回归问题用恒等函数，分类问题用softmax函数。

感知机就是用的阶跃函数去激活的，那么用其他激活函数的就是神经网络了！

（1）阶跃函数

1、Python实现阶跃函数

def step_function(x):
    if x > 0:
        return 1
    else:
        return 0

2、用NumPy实现阶跃函数(输入为正，输出1；输入为负，输出0)

def step_function(x):
    y = x > 0
    return y.astype(np.int) 
    # 把数组y的元素类型从布尔型转换为 int型


# 直接如下也对
def step_function(x):
    np.array(x > 0, dtype=np.int)

3、画出阶跃函数

import numpy as np
import matplotlib.pylab as plt

# 阶跃函数的实现
def step_function(x):
    return np.array(x > 0, dtype=np.int)

x = np.arange(-5.0,5.0,0.1) # 设置x轴范围、步进，创建创建array数组
y = step_function(x) # 给出x,y的关系
plt.plot(x,y) # 画图函数plot
plt.ylim(-0.1,1.1) # 设定y坐标轴的范围
plt.show() # 显示结果

（2）sigmoid(逻辑回归常用)

1、sigmoid函数的实现

# sigmoid函数的实现
def sigmoid(x): # x 可以是NumPy数组
    return 1/(1+np.exp(-x))

2、画出sigmoid函数

# 画出sigmoid函数
x = np.arange(-5.0,5.0,0.1)
y =sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

sigmoid函数的平滑性对神经网络的学习具有重要意义。

（3）ReLU函数（线性整流函数：最近使用的激活函数）（Rectified Linear Unit）

1、ReLU函数的实现

def ReLU(x):
    return np.maximum(0,x)

2、画出ReLU函数

x = np.arange(-5.0,5.0,0.1)
y =ReLU(x)
plt.plot(x,y)
plt.ylim(-1.0,5.0)
plt.show()

输出层使用的激活函数选择要根据求解问题的性质决定。
回归问题：用恒等函数，直接输出
分类问题：
二元分类问题：用sigmoid函数
多元分类问题：用softmax函数（下节讨论）

（4）softmax函数（一般用于多元分类问题）

softmax函数实现

softmax激活函数实现，一般用于多元分类

def softmax(a): # 传入数组a
    exp_a = np.exp(a)
    exp_sum = np.sum(exp_a)
    y = exp_a / exp_sum
    return y

遇到指数函数要当心

防止溢出，加个或减去个C，结果不变
softmax激活函数改善，防止溢出，加个或减去个C

def softmax(a): # 传入数组a
    c = np.max(a)
    exp_a = np.exp(a - c)
    exp_sum = np.sum(exp_a)
    y = exp_a / exp_sum
    return y

softmax函数的输出值的总和是1，所以可以把softmax函数的输出解释为“概率”。

# function.py
# 一般用于多分类任务的激活函数
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0) # 列方向
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))

axis = 1 行方向
axis = 0 列方向

注意：矩阵的第0维是列方向，第1维是行方向。

比如：
参数 axis=1。这指定了在100 × 10的数组中，沿着第1维方向（以第1维为轴）找到值最大的元素的索引（第0维对应第1个维度）

5、损失函数

定义

• 损失函数是表示神经网络性能的“有多坏（恶劣程度）”的指标，即当前的神经网络对监督数据（训练数据）在多大程度上不拟合，在多大程度上不一致。恶劣程度越小，越好。

• 神经网络以某个指标作为线索寻找最优权重参数，这个指标就是 损失函数（loss function）

• 损失函数一般用均方误差和交叉熵误差等。

• 当使用sigmoid作为激活函数的时候，常用交叉熵损失函数而不用均方误差损失函数。

（1）均方误差

python实现均方误差

def mean_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)

（2）交叉熵误差

python实现交叉熵误差

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

（3）mini-batch版交叉熵误差的实现

• 用随机选择的小批量数据（mini-batch）作为全体训练数据的近似值。（就像抽样、采样进行人口普查一样）

# 可以同时处理单个数据和批量数据（数据作为batch集中输入）两种情况的函数
def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    return -np.sum(t * np.log(y + 1e-7)) / batch_size

• 当监督数据 t 是标签形式（非one-hot表示，而是像“2”“7”这样的标签）时，交叉熵误差可通过如下代码实现

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

为何要设定损失函数？

• 我们的目标是获得使识别精度尽可能高的神经网络，那可以用识别精度作为指标吗？
  • 为了找到使损失函数的值尽可能小的地方，需要计算参数的导数（梯度），以这个导数为指引，逐步更新参数的值。
  • 如果导数的值为负，通过使该权重参数向正方向改变，减小损失函数的值；
  • 如果导数的值为正，则通过使该权重参数向负方向改变，减小损失函数的值。
  • 当导数的值为0时，无论权重参数向哪个方向变化，损失函数的值都不会改变，此时该权重参数的更新会停在此处。
  • 那么如果以识别精度为指标，则参数的导数在绝大多数地方都会变为0。则无法更新参数。
  • 综上，需要设定损失函数来描述神经网络的好坏。