单调栈算法笔记

单调栈

目录

名词解释

实现

功能

例题

 

---

名词解释

---

要了解什么是单调栈，我们可以分开来理解一下什么叫“单调”，什么叫“栈”。

栈

先引入百度百科中栈的定义

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

用自己的话来说，栈是一种数据结构，其主要特点就是先进后出。

栈的具体操作这里就不细讲。

单调

小学五年级的学生都知道单调是什么意思。

一个递增的函数，被称为是单调递增函数；一个递减的函数，被称为是单调递减函数。而两者统称为单调函数。

而在这里，单调指的就是递增或递减。

单调栈

那么合起来，单调栈则是指这个栈内的元素单调，从底部到顶部要么单调递增，要么单调递减。

 

实现

---

要实现一个单调栈其实特别简单，以单调递增的栈为例子：

假设现在有7个元素，分别为6 9 7 9 10 4 8。

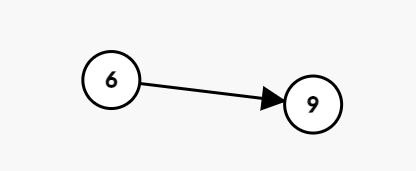
那么首先进入栈里的是元素6，先入栈。

然后是元素9,9>6，因为建立的是一个单调递增的栈，所以9也入栈。

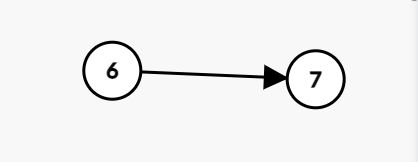
然后进来了一个7，由于7比9小，为了形成一个单调递增的栈，则需要把9去掉。

然后栈内还有6，7比6大，为了形成一个单调递增栈，所以直接让7入栈 。

那么现在已经栈内的情况为：

后面的元素9比7大，所以直接入栈。

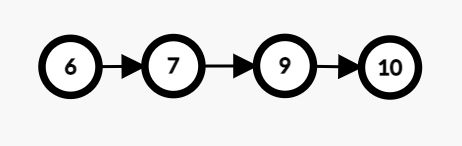
然后的元素10比9大，所以也直接入栈。

然后栈内的情况就如下图所示：

下一个元素是4,4先和栈顶的元素10比较，10比4大，所以10出栈。

然后再比较10出栈后的栈顶元素9，9仍然比4大，所以9出栈。

在比较此时的栈顶元素7，7还是比4大，所以7出栈。

随后比较此时栈顶元素6，6比4大，所以也出栈。但此时栈已经为空，所以将4入栈。

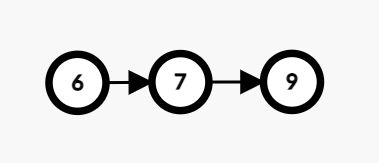
然后再来一个元素8，8比栈顶元素4要大，所以8入栈，最后栈内情况如下图所示

 

所以实现一个单调栈，其实无非就三步：判断，出栈，入栈。

 

功能

---

那么知道如何实现一个单调栈以后，我们能用单调栈来做什么呢？

大家先思考一个问题，实现单调栈的时候，最重要的部分是哪？ 判断是否能够入栈使得栈内元素单调。

对的，我们需要操作的部分就是判断。

当一个新的元素准备入栈时，我们与栈顶元素进行判断，如果该元素入栈后使得单调性破坏，则我们的步骤则是不断地让栈顶元素出栈，直到新的元素入栈后继续保持栈内元素的单调性。

而与栈顶元素破坏栈内元素单调性的这个矛盾，我认为便是单调栈功能的所在点。

这样子的话，使用单调栈，就可以找到一段连续数列中破坏单调性的点。

例如在一组数据8 3 5 1 9中，需要你找到每个数左边第一个比它大的数。

我们可以用最笨的方法，两个for循环，这样子需要O（）的时间复杂度。

for(int i=1;ia[i])
        {
            cout<

很容易理解，用单调栈来实现的话，可以做到O（n）的时间复杂度。

我们建立一个单调递减的栈，一直维护着单调递减。当来了一个破坏单调性的元素时，也就是比栈顶元素大的元素，则开始比较。如栈顶的元素比新元素小，则这个新元素就是这个栈顶元素左边的第一个比它大的数。然后这个栈顶元素就找到答案了，就出栈，然后再比较下一个栈顶元素。

用样例8 3 5 1 9，一开始栈内维护着“8 3”，5比3大，则5是3左边第一个比它大的元素，出栈。然后比较5和8，因为比5大的有可能比8大，并且要维持一个单调递减的栈，则5入栈。1也类似，则此时栈内元素为“8 5 1”。当9要来时，9比此时的栈顶元素1大，9就是第一个比它大的数，然后1出栈。随后比较5，最后比较8，都和元素1一样的结果，所以最后就解决了问题。

这个问题也是洛谷里单调栈的模板题。

 

例题

---

 

洛谷P5788模板题

这题就是一个单调栈的模板题，找每个元素左边第一个比它大的元素的下标。

#include
#include
using namespace std;
const int oo=3000005;
int n,a[oo],f[oo];
stack s;
void read_in()
{
	ios::sync_with_stdio(false),cin.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
	  cin>>a[i];
	for(int i=1;i<=n;i++)
	  f[i]=i;
}
void work()
{
	for(int i=1;i<=n;i++)
	{
		if(s.empty() || a[s.top()]>a[i])
		  s.push(i);
		else
		{
			while(!s.empty() && a[s.top()]

 

洛谷P2947

这题也是找左边第一个比它高的牛，也是一样的。 

#include
#include
#include
using namespace std;
const int oo=100005;
int n,a[oo],ans[oo];
stack s;
void read_in()
{
	ios::sync_with_stdio(false),cin.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
	  cin>>a[i];
}
void work()
{
	for(int i=1;i<=n;i++)
	{
		if(s.empty() || a[s.top()]>=a[i])
		  s.push(i);
		else
		{
			while(!s.empty() && a[s.top()]

 

SP1805

经典的矩阵面积覆盖问题。

这道题我们可以理解为，找以目前这个数为最小值，左边第一个比它小的数的位置和右边第一个比它小的数的位置。以这个数为最小值能组成的最大矩阵面积就是这两者之间的距离为底，目前的数值为高的矩形的面积。然后再比较所有答案的最大值。

#include
#include
#include
using namespace std;
stack s;
const int oo=100005;
int n;
long long l[oo],r[oo],a[oo],ans,A;
void read_in()
{
	ans=-1;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		l[i]=r[i]=i;
	}
}
void work()
{
	for(int i=1;i<=n;i++)
	{
		
		if(s.empty() || a[s.top()]a[i])
			{
				l[i]=l[s.top()];
				r[s.top()]=i-1;
				s.pop();
			}
			s.push(i); 
		}
		
	}
	while(!s.empty())
	{
		r[s.top()]=n;
		s.pop();
	}
	for(int i=1;i<=n;i++)
	  ans=max(ans,(r[i]-l[i]+1)*a[i]);
	
}
int main()
{
	while(cin>>n)
	{
		if(n==0)
		  break;
		read_in();
		work();
		if(A!=0)
		  cout<<'\n';
		cout<

 

洛谷P1823

这题很让我头疼，因为这个涉及了新元素与栈顶元素相同时的处理问题。具体是什么问题大家可以做做看。我用STL的stack做超时最后几个点了，然后找到了4年前自己还不会STL时用数组模拟栈的程序，A掉了。下面贴超时的程序供大家思考和改进。（其实是我改不出2333希望有大佬捞我一把）

#include
#include
#include
using namespace std;
const int oo=500005;
stack s;
int n;
long long a[oo],ans,same;
void read_in()
{
	ios::sync_with_stdio(false),cin.tie(0); 
	cin>>n;
	for(int i=1;i<=n;i++)
	  cin>>a[i];
}
void work()
{
	for(int i=1;i<=n;i++)
	{
		if(s.empty())
		{
			s.push(i); 
			continue;
		}
		if(a[s.top()]>a[i])
		{
			ans++;
			s.push(i); 
		}
		else
		{
			while(!s.empty() && a[s.top()]

 

---

本人不才，单调栈只能稍微总结到这，如果有什么问题不懂，可以问问我，我会尽力回答。如果文章有什么问题或者我有表达错的地方，也希望能够指出。

谢谢大家，共同努力进步。