python用keras实现线性回归模型

Keras是一个用于构建和训练深度学习模型的高阶API。为了实现猫狗大战，对keras进行学习，今天用keras实现一个简单的线性回归模型。

首先导入库

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential #导入keras中的Sequential API。
from tensorflow.keras.layers import Dense      #导入keras中的全连接层

这就是等下要用到的库了，这里用到的是基于TensorFlow2.x的keras。

然后要做的就是导入训练集了。在这里先给定一个线性关系 y = 2.001x + 10.112 。 根据这一线性关系来创建训练集和测试集，代码如下。

X_data = np.random.rand(2000) #创建一个大小2000的随机数据集
Y_data = 2.001*X_data + 10.112   #给定线性关系
X_train, Y_train = X_data[:1800], Y_data[:1800]     # 前1800组数据为训练数据集
X_test, Y_test = X_data[1800:], Y_data[1800:]       # 后1800组数据为测试数据集

本来只创建了大小250的数据集，但经学长提醒，训练集越大模型精确度越高，这也点醒了自己。

接下来我们用到keras模型中的Sequential模型。

Sequential模型的用法：

首先是add(layer) 添加层：在层堆栈的顶部添加层实例，我们使用调用出的Dense（全连接层）。

而后是compile 模型配置，先列出以下参数，其他参数不涉及暂不说明

compile(
    optimizer='sgd',  			    # 优化器的名称或优化器实例，这里表示优化器为sgd即随机梯度下降
    loss='mse',						# 表示损失函数，mse代表的损失函数下文讲述
    								# 使用不同的损失，模型最小化的损失值将是所有独立损失的总和。
    metrics=None                    # 在训练和测试期间的模型评估标准。								
)

还有evaluate 评价：顾名思义对模型进行评价

evaluate(
    x=None,								# 输入值
    y=None,								# 目标值
    batch_size=None,					# 每次梯度更新的样本数
)

暂时用到的就这些，接下来用代码实现。

model = Sequential()   #使用keras中的Sequential模型
model.add(Dense(units=1, input_dim=1))   #增加一个dense全连接层
model.compile(optimizer='sgd', loss='mse')   #optimizer表示优化器为sgd即随机梯度下降，损失函数选择mse即方差

这里梯度下降法和损失函数之前博客中有讲过，在此不多加赘述，只是提一点，在这里损失函数表示如下
$$L(p^{(i)},y^{(i)})=(p^{(i)}-y^{(i)}{)}^2$$
成本函数就是
$$J(w,b)=\frac{1}{m}\sum _{i=1}^m(p^{(i)}-y^{(i)}{)}^2$$
使用keras我们可以直接完成一次梯度下降，接下来就是通过迭代进行训练了，代码如下

for step in range(3000):   #3000表示进行3000次训练，过小拟合效果不会很好，当然也不能太大，否则会过度拟合
   train_cost = model.train_on_batch(X_train, Y_train)
   if step % 100 == 0:    #每100次打印一次训练集的损失函数值
       print('训练集真值差:', train_cost)

这里的训练集真值差即损失函数值，每100次进行打印我们可以观察随着训练模型的准确度变化。根据损失函数的定义我们可以知道当这个值越小，模型与我们期望的就越接近。

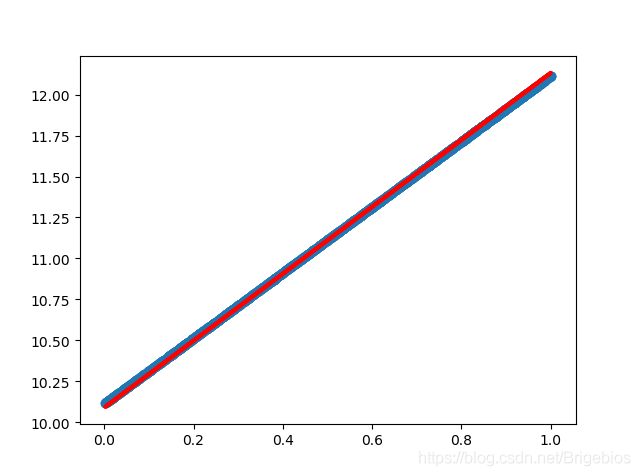
接着我们打印出拟合图像

y_pre = model.predict(X_train)
plt.scatter(X_train, Y_train)
plt.plot(X_train, y_pre, 'r-', lw=3)
plt.show()   #显示图像拟合情况

这里用到predict函数为输入样本生成输出预测。

结果如下：

可以看到拟合效果还不错（蓝点是训练集根据线性关系生成的，红线是根据模型得到的预测线性关系）。

最后我们打印出模型的线性关系进行对比，再把测试集的损失值打印出来，评价模型好坏，代码如下。

w, b = model.layers[0].get_weights()    #同样利用keras得到加权值，分配到w和b中
print('线性关系为:','y =', w[0][0],'x +', b[0]) #打印出模型训练出的线性关系，来和我们定义的线性关系对比

test_cost = model.evaluate(X_test, Y_test, batch_size=200)     #在测试集上进行模型评价
print('测试集真值差:', test_cost)

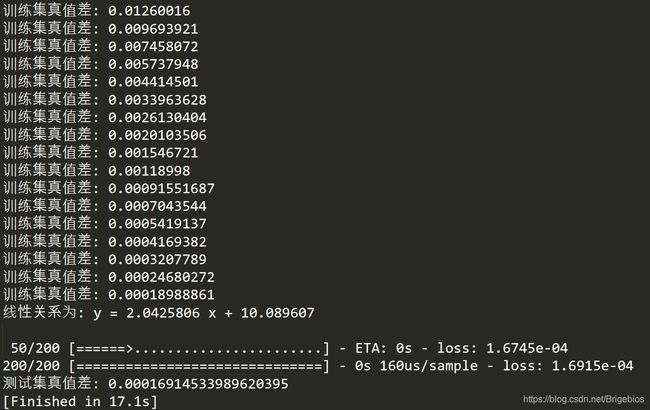
最后的代码运行结果如下：

最后的线性关系打印出来是 y = 2.0425806 x + 10.089607 ，与我们定义的y = 2.001x + 10.112 有些微差距，但可以通过增加训练集或者加大迭代次数提高模型精确度，在此就不多加展示了。

今天对keras进行了一个简单的应用，下步会一步步实现猫狗大战。