AI学习笔记(六)三维计算机视觉与点云模型
AI学习笔记之三维计算机视觉与点云模型
- 立体视觉
-
- 立体视觉的概念
- 立体视觉的原理
- 单目系统
- 双目系统和视差
- 对极几何约束
- SIFT
-
- sift特征的特点
- sift算法总体介绍
- sift特征提取和匹配具体步骤
-
- 1、生成高斯差分金字塔(DOG金字塔),尺度空间构建
-
- sift尺度空间
- sift图像金字塔
-
- 高斯金字塔
- 构建尺度空间
-
- DOG金字塔
- 2、空间极值点检测(关键点的初步查探)
-
- 尺度空间极值检测
- 高斯金字塔的k值
- 3、确定关键点的精确定位
- 4、稳定关键点方向信息分配
- 5、关键点描述
- 6、特征点匹配
- 点云模型与三维重建
-
- 点云模型
-
- 点云与三维图像
- 点云的概念
- 点云的内容
- 点云处理的三个层次
-
- 1、低层次处理方法
- 2、中层次处理方法
- 3、高层次处理方法
- Spin image
-
- 生成spin image的步骤
- 点云滤波
- 三维重建
-
- SfM与三维重建
-
- 增量式SfM
- 全局式SfM
- 混合式SfM
- SfM的劣势
- OpenMVG
立体视觉
立体视觉的概念
立体视觉是一种计算机视觉技术,其目的是从两幅图或两幅以上的图像中推理处图像中每个像素点的深度信息。其可应用于机器人、辅助驾驶/无人驾驶、无人机等等。
立体视觉的原理
立体视觉借鉴了人类双眼的“视差”原理,即左、右眼对于真实世界某一物体的观测是存在差异的,我们的大脑正式利用了左、右眼的差异,使得我们能够辨识物体的远近。(视差)
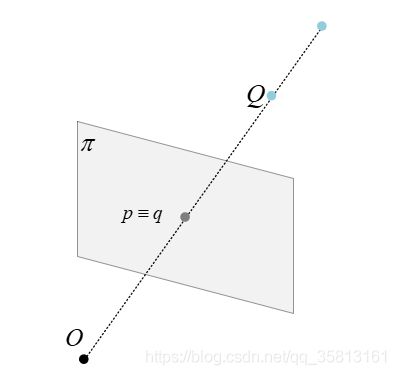
单目系统
双目系统和视差

给定一幅图像上的一个特征,他在另一幅图像上的匹配师徒一定在对应的极线上
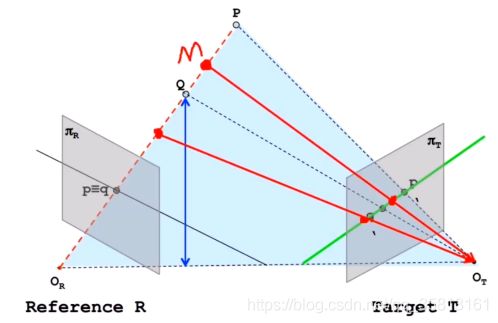

根据三角形相似定理:( △ P p p ′ ∼ △ P O R O T \bigtriangleup Ppp'\sim\bigtriangleup PO_RO_T △Ppp′∼△POROT)
B Z = p p ′ Z − f = B − ( X R − W 2 ) − ( W 2 − X T ) Z − f = B + X T − X R Z − f \frac BZ=\frac{pp'}{Z-f}=\frac{B-(X_R-\frac W2)-(\frac W2-X_T)}{Z-f}=\frac{B+X_T-X_R}{Z-f} ZB=Z−fpp′=Z−fB−(XR−2W)−(2W−XT)=Z−fB+XT−XR
Z = B ∗ f X T − X R = B ∗ f d Z=\frac{B\ast f}{X_T-X_R}=\frac{B\ast f}d Z=XT−XRB∗f=dB∗f
Z = B ⋅ f x R − x T = B ⋅ f D Z=\frac{B\cdot f}{x_R-x_T}=\frac{B\cdot f}D Z=xR−xTB⋅f=DB⋅f
D也就是我们通常所说的视差(disparity)

对极几何约束
- 极平面: O 1 , O 2 , P O_1,O_2,P O1,O2,P三个点确定的平面;
- 极点: O 1 , O 2 O_1,O_2 O1,O2连线与像平面 l 1 , l 2 l_1,l_2 l1,l2的交点 e 1 , e 2 e_1,e_2 e1,e2
- 基线(baseline): O 1 O 2 O_1O_2 O1O2
- 极线: 极平面与两个像平面之间的交线 l 1 , l 2 l_1,l_2 l1,l2

SIFT
Sift(尺度不变特征变换:Scale Invariant Feature Transform),其提取图像的局部特征,在尺度空间寻找极值点,并提取处其位置、尺度、方向信息。Sift的应用范围包括物体识别、机器人地图感知与导航、影像凭借、3D模型建立、手势识别、影像追踪等。
sift特征的特点
1、对旋转、尺度缩放、亮度变化保持不变,对视角变化、噪声等也存在一定程度的稳定性;
2、对特性,信息量丰富,使用与在海量特征数据中进行快速,精准的匹配;
3、多量性,即使少数几个物体也可以产生大量的Shift特征向量;
4、可扩展性,可以很方便的与其他形式的特征向量进行联合。
sift算法总体介绍
sift算法的实质是在不同的尺度空间上查找关键点(特征点),计算关键点的大小、方向、尺度信息,利用这些信息组成关键点对特征点进行描述的问题。sift所查找的关键点都是一些十分突出,不会因光照,仿射变换和噪声等因素而变换的“稳定特征点,如角点、边缘点、暗区的亮点以及亮区的暗点等。匹配的过程就是对比这些特征点的过程。
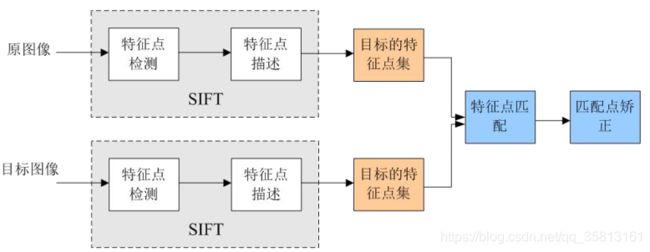
sift特征提取和匹配具体步骤
1、生成高斯差分金字塔(DOG金字塔),尺度空间构建
sift尺度空间
尺度空间,在摄像头中,计算机无法分辨一个景物的尺度信息。而人眼不同,除了大脑里已经对物体有了基本的概念(例如正常人在十几米之外看到苹果,和在近距离看到苹果,都能认出是苹果)以外,人眼在距离物体近是,能够获得物体足够多的特性,在距离物体远时,能够忽略细节,例如,近距离看一个人脸能看到毛孔,距离远了看不到毛孔等等。
在图片信息当中,分辨率都是固定的,要想得到类似人演的效果,就要把图片弄成不同的分辨率,制作成图像金字塔来模拟人眼的功能,从而在其他图片中进行特征识别时,能够像人眼睛一样,即便要识别物体尺寸大小或者变小,也能够识别出来。
尺度空间即试图在图像领域中模拟人眼观察物体的概念和方法。例如,观察一棵树,关键在于我们想要观察室树叶子还是整棵树;如果是一整棵树(相当于大尺度情况下观察),那么就应该去除图像的细节部分。如果是树叶(小尺度情况下观察),那么就该观察局部细节特征。
sift图像金字塔
通俗地说,尺度空间就详单与一个图片需要获得多少分辨率的量级。如果把一个图片从原始分辨率不停地对其分辨率进行减少,然后讲这些图片摞在一起,可以看出一个四棱锥的样式。这个东西就叫做图像金字塔。
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行尺度像素采样的方式,进行N各不同分辨率的图像,把具有高级别分辨率图像放在底部,以金字塔形状排列,往上是一些类像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔。

获得图像金字塔一般包括两个步骤:
1、利用低筒滤波器平滑啊图像(高斯滤波)
2、对平滑图像进行抽样(采样)
有两种采样方式(分辨率逐渐升高)和下采样(分辨率逐渐降低)。
主要思想是通过对原始图像进行尺度变换,获得图像多尺度下的尺度空间表示序列,对这些序列进行尺度空间主轮廓的提取,并以该主轮廓作为一种特征向量,实现边缘、角点检测不同分辨率上的关键点提取等。
各尺度图像的模糊度逐渐变大,能够模拟人在距离目标由近到远时目标物体在视网膜上的香橙过程。
尺度空间构建的基础识DOG金字塔,DOG金字塔构建的基础就是高斯金字塔。
高斯金字塔
高斯金字塔在sift算子中提出来的概念,首先高斯金字塔并不是一个金字塔,而是有很多组(Octave)金字塔构成,并且每组金字塔都包含若干层(Interval)
高斯金字塔构建过程:
1、先将图像扩大一倍之后作为高斯金字塔的第1组第1层,经第1组第1成层图像经高斯卷纸机(其实就是高斯平滑或称高斯滤波)之后作为第1组金字塔的第二层;
2、将 σ \sigma σ乘以一个比例系数 k k k,得到一个新的平滑因子 σ = k ∗ σ \sigma=k*\sigma σ=k∗σ,用它来平滑第1组第2层图像,结果图像作为第3层;
3、如此这般重复,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样。他们对应的平滑系数分别为: 0 , σ , k σ , k 2 σ , k 3 σ ⋯ k L − 2 σ 0,\sigma,k\sigma,k^2\sigma,k^3\sigma\cdots k^{L-2}\sigma 0,σ,kσ,k2σ,k3σ⋯kL−2σ;
4、将第一组倒数第三层图像做比率因子为2的降采样,得到的图像作为第2组的第一层,然后对第2组的第1层退昂做平滑因子为 σ \sigma σ的高斯平滑,得到第2组的第2层,就像步骤2一样,如此得到第2组的L层图像,通组内它们的尺寸是一样的,对应的平滑系数分别为: 0 , σ , k σ , k 2 σ , k 3 σ ⋯ k L − 2 σ 0,\sigma,k\sigma,k^2\sigma,k^3\sigma\cdots k^{L-2}\sigma 0,σ,kσ,k2σ,k3σ⋯kL−2σ。但是在尺寸方面第2组是第1组图像的一半。
G ( x , y ) = 1 2 π σ 2 e x p { − ( x − x 0 ) 2 + ( y − y 0 ) 2 2 σ 2 } G(x,y)=\frac1{2\pi\sigma^2}exp\{-\frac{ {(x-x_0)}^2+{(y-y_0)}^2}{2\sigma^2}\} G(x,y)=2πσ21exp{ −2σ2(x−x0)2+(y−y0)2}
反复执行,就可以得到一共O组,每层L层,共计O*L个图像,这些图像就构成了图像金字塔。
- 在同一组内,不同层图像的尺寸是一样的,后一层推向的高斯平滑因子 σ \sigma σ是前一层图像平滑因子的 k k k倍;
- 在不同组内,后一组第一个图像是前一组倒数第三个图像二分子一采样,图像大小是前一组的一半;
构建尺度空间
在高斯金字塔中一共生成O组L层不同尺度的图像,这两个量合起来(O,L)就构成了高斯金字塔的尺度空间,也就是说一高斯金字塔的组O作为二维空间坐标系的一个坐标,不同层L作为另一个坐标,则给定的一组坐标(O,L)就可以唯一确定高斯金字塔中的一幅图像。
尺度空间的形象表述:
- 图像尺度空间中k前的稀疏n表示第一组推向尺寸是当前组推向尺寸的n倍。
 sift算法在构建尺度空间时候采取高斯核函数进行滤波,使原始图像保存最多的细节特征,经过高斯滤波后细节特征逐渐减少来模拟大尺度情况下的特征表示。
sift算法在构建尺度空间时候采取高斯核函数进行滤波,使原始图像保存最多的细节特征,经过高斯滤波后细节特征逐渐减少来模拟大尺度情况下的特征表示。
利用高斯核函数进行滤波的主要原因有两个:
(1)高斯核函数是唯一的尺度不变核函数;
(2)Dog核函数可以近似为Log函数,这样可以使特征提取更加简单。
其实尺度空间图像生成就是当前图像与不同尺度核函数 σ \sigma σ进行卷积运算后产生的图像。
L ( x , y , σ ) L(x,y,\sigma) L(x,y,σ),定义为原始图像(x,y)与一个可变尺度的2维高斯核函数 G ( x , y , σ ) G(x,y,\sigma) G(x,y,σ)卷积运算。
G ( x i , y i , σ ) = 1 2 π σ 2 e x p { − ( x − x 0 ) 2 + ( y − y 0 ) 2 2 σ 2 } L ( x , y , σ ) = G ( x , y , σ ) ∗ I ( x , y ) G(x_i,y_i,\sigma)=\frac1{2\pi\sigma^2}exp\{-\frac{ {(x-x_0)}^2+{(y-y_0)}^2}{2\sigma^2}\}\\L(x,y,\sigma)=G(x,y,\sigma)\ast I(x,y) G(xi,yi,σ)=2πσ21exp{ −2σ2(x−x0)2+(y−y0)2}L(x,y,σ)=G(x,y,σ)∗I(x,y)
DOG金字塔
尺度空间构建的基础是DOG金字塔,DOG金字塔构建的基础是高斯金字塔。
差分金字塔,DOG(Difference of Gaussian)金字塔是在高斯金字塔的基础上构建起来的,其实生成高斯金字塔的目的就是为了构建DOG金字塔。
DOG金字塔的第1组第1层是由高斯金字塔的第1组第2层间第1组第1层得到的,以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。概括为DOG金字塔的第o组第I层图像是由高斯金字塔的第o组第l+1层减第o组第l层得到的。
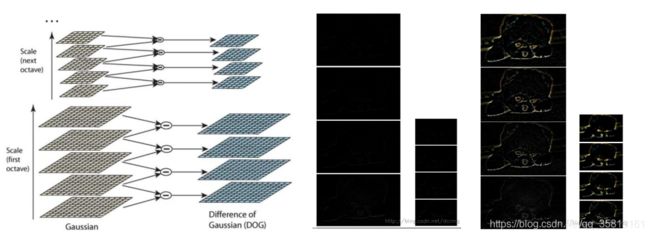
2、空间极值点检测(关键点的初步查探)
尺度空间极值检测
特征点是由DOG空间的局部极值点组成的,为了寻找DOG函数极值点,每一个像素点要和它所有的相邻点比较,看其是否比它的图像域和尺度域的相邻点大或者小。
如下图,中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9x2个共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点。
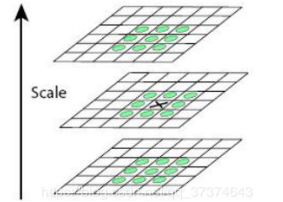
注意,局部极值点都是在同一个组当中进行的,所以肯定有这样的问题,某一组当中的第一个图和最后一个图层没有前一张图和下一张图,那该怎么计算?解决办法用高斯模糊,在高斯金字塔多“模糊”出三张来凑数,所以在DOG中多出两张。
高斯金字塔的k值
k = 2 1 s k=2^\frac1s k=2s1s:魅族图像中检测s个尺度的极值点。(实际计算时,s通常在3到5之间)
sift算法中生成高斯金字塔的规则(M,N为原始图像的行数和列数)
设高斯金字塔共包含O组图像,魅族图像有s+3层,则 O = log 2 ( m i n { M , N } ) − 3 O=\log_2(min\{M,N\})-3 O=log2(min{ M,N})−3
3、确定关键点的精确定位
DOG值对噪声和边缘比较敏感,所以在第2步的尺度空间中检测到的局部极值点还要经过进一步的筛选,去除不稳定和错误检测出的极值点。
利用阈值的方法来限制,在opencv中为contrastTreshold。
4、稳定关键点方向信息分配
稳定的极值点是在不同尺度空间下提取的,这保证了关键点的尺度不变性。
为关键点分配方向信息所需要的解决的问题是使得关键点对图像角度和旋转具有不变性。
方法:获取关键点所在尺度空间的邻域,然后计算该区域的梯度和方向,根据计算得到的结果创建方向直方图,直方图的峰值为主方向的参数,其他高于主方向百分之80的方向被判定为辅助方向,这样设定对稳定性有很大帮助。

对于任一关键点,其梯度负值表述为:
m ( x , y ) = ( L ( x + 1 , y ) − L ( x − 1 , y ) ) 2 + ( L ( x , y + 1 ) − L ( x , y − 1 ) ) 2 m(x,y)=\sqrt{(L(x+1,y)-L{(x-1,y))}^2+(L(x,y+1)-L{(x,y-1))}^2} m(x,y)=(L(x+1,y)−L(x−1,y))2+(L(x,y+1)−L(x,y−1))2
梯度方向为:
θ ( x , y ) = tan − 1 [ L ( x , y + 1 ) − L ( x , y − 1 ) L ( x + 1 , y ) − L ( x − 1 , y ) ] \theta(x,y)=\tan^{-1}\left[\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)}\right] θ(x,y)=tan−1[L(x+1,y)−L(x−1,y)L(x,y+1)−L(x,y−1)]
5、关键点描述
对于每一个关键点,都拥有位置、尺度以及方向三个信息。所以具备平移、缩放和旋转不变性。为每个关键点建立一个描述符,用一组向量将这个关键点描述出来,使其不随各种变化而变化,比如光照变化、视角变化等等描述不但包含关键点,也包干关键点周围对其有贡献的邻域点。
描述的思路是:对关键点周围像素区域分块,计算块内梯度直方图,生成具有独特性的向量,这个向量是该区域图像信息的一种抽象表达。
如下图:对于22块,二米快的所有像素点的灰度做高斯加权,每块最终取8个方向,即可以生成228维度的向量,以这22*8维向量作为中心关键点的数学描述。
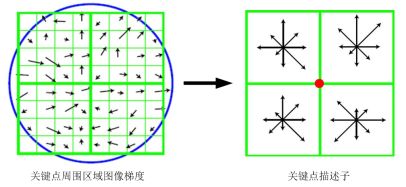
Lowe实验结果表明,对于每个关键点采用 4 × 4 × 8 = 128 4\times4\times8=128 4×4×8=128维向量表征,综合效果最优(不变性与独特性)。

6、特征点匹配
特征点的匹配是通过计算两组特征点的128维的关键点的欧氏距离实现的。
欧式距离越小,则相似度越高,当欧式距离小于设定的阈值时,可以判定为匹配成功。
具体步骤:
1、分别对模板图(参考图,reference image)和实时图(观测图,observation image)建立关键点描述自己和。目标的识别时通过两点集内关键点描述子的对比来完成。具有128维的关键点描述子的相似性度量采用欧式距离。
2、匹配可采取穷举法完成。
注意:
Python中的sift函数注册了专利,在商业用途上是收费的。将在opencv>3.4.3中不再提供。
较低版本安装:
pip install opencv-python == 3.4.2.16
pip install opencv-contrib-python== 3.4.2.16
sift关键点检测代码如下:
import cv2
import numpy as np
img = cv2.imread("lena.png")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
sift = cv2.xfeatures2d.SIFT_create()
keypoints, descriptor = sift.detectAndCompute(gray, None)
# cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS对图像的每个关键点都绘制了圆圈和方向。
img = cv2.drawKeypoints(image=img, outImage=img, keypoints=keypoints,
flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS,
color=(51, 163, 236))
# img=cv2.drawKeypoints(gray,keypoints,img)
cv2.imshow('sift_keypoints', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
import cv2
import numpy as np
def drawMatchesKnn_cv2(img1_gray, kp1, img2_gray, kp2, goodMatch):
h1, w1 = img1_gray.shape[:2]
h2, w2 = img2_gray.shape[:2]
vis = np.zeros((max(h1, h2), w1 + w2, 3), np.uint8)
vis[:h1, :w1] = img1_gray
vis[:h2, w1:w1 + w2] = img2_gray
p1 = [kpp.queryIdx for kpp in goodMatch]
p2 = [kpp.trainIdx for kpp in goodMatch]
post1 = np.int32([kp1[pp].pt for pp in p1])
post2 = np.int32([kp2[pp].pt for pp in p2]) + (w1, 0)
for (x1, y1), (x2, y2) in zip(post1, post2):
cv2.line(vis, (x1, y1), (x2, y2), (0, 0, 255))
cv2.namedWindow("match", cv2.WINDOW_NORMAL)
cv2.imshow("match", vis)
img1_gray = cv2.imread("iphone1.png")
img2_gray = cv2.imread("iphone2.png")
#sift = cv2.SIFT()
sift = cv2.xfeatures2d.SIFT_create()
#sift = cv2.SURF()
kp1, des1 = sift.detectAndCompute(img1_gray, None)
kp2, des2 = sift.detectAndCompute(img2_gray, None)
# BFmatcher with default parms
bf = cv2.BFMatcher(cv2.NORM_L2)
matches = bf.knnMatch(des1, des2, k=2)
goodMatch = []
for m, n in matches:
if m.distance < 0.50 * n.distance:
goodMatch.append(m)
drawMatchesKnn_cv2(img1_gray, kp1, img2_gray, kp2, goodMatch[:20])
cv2.waitKey(0)
cv2.destroyAllWindows()
点云模型与三维重建
点云模型
点云与三维图像
三维图像是一种特殊的信息表达形式,其特征是表达的空间中三个维度的数据。和二维图像相比,三维图像借助第三个维度的信息,可以实现天然的物体和背景解耦。
对于视觉出测量来说,物体的二维信息往往随射影方式而变化,但其三维特征对不同测量方式具有更好的统一性。
与相片不同,三维图像是对一类信息的同城,信息还需要有具体的表现形式,其表现形式包括:深度图(一灰度表达物体与相机的距离),几何模型(由CAD软件建立),点云模型(所有逆性工程设备都将物体采样成点云)。
点云数据是最常见也是最基础的三维模型。
点云:扫描资料以点的形式,每一个点包含有三维坐标,有些可能含有颜色信息(RGB)或反射强度信息(Intensity)。
点云的概念
点云是在同一空间参考系下表达目标空间分布和目标表面特性的海量点集合,自获取物体表面每个采样点的空间坐标后,得到的是点的集合,称之为“点云”(Point Cloud)。
点云的内容
根据激光测量原理得到的点云,包含三维坐标(XYZ)和激光反射强度。强度信息与目标的表面材质、粗糙度、入射方向、以及仪器的放射能量,激光波长有关。根据摄影测量原理得到的点云,包括三维坐标(XYZ)和颜色信息(RGB)。
结合激光测量和摄影测量原理得到点云,包括三维坐标(XYZ)、激光反射强度(Itensity)和颜色信息(RGB)。
点云处理的三个层次
1、低层次处理方法
1、滤波方法:双边滤波、高斯滤波、条件滤波、直通滤波、随机采样一致性滤波。
2、关键点:ISS3D、Harris3D、NARF、SIFT3D
2、中层次处理方法
1、特征描述:法线和曲率的计算、特征值分析、SHOT、FPFH、3D Shape Contex、Spin Image
2、分割与分类
分割:区域生长、Ransac线面提取、全局优化平面提取、K-Means、Normalize Cut(Context based)、3D Hough Transform(线、面提取)、连通分析
分类:基于点的分类、基于分割的分类、基于深度学习的分类(PointNet、OctNet)
3、高层次处理方法
1、配准:点云配准分为粗配准(Coarse Registration)和精配准(Fine Registration)两个阶段。
精配准的目的是在粗配准的基础上让点云之间的空间位置差别化最小
粗配准是指在电鱼相对位置完全未知的情况下对点云进行配准,可以为精准配准提供良好的初始值。
基于穷举搜索的配准方法:遍历整个变换空间可以选取是误差函数最小化的变换关系或者雷剧处使最多点对满足的变换关系。如RANSAC配准方法、四点一致集配准方法(4-Point Congruent Set,4PCS)、Super4PCS算法等。
基于特征匹配的配准方法:通过被测物体本身所具备的形态特性构建点云间的匹配对应、然后采用相关算法对变换关系进行估计。如基于点FPFH特征的SAC-IA、FGR等算法、基于点SHOT特征的AO算法以及基于线特征的ICL等
2、SLAM图优化
Ceres(Google的最小二乘优化库),g2o、LUM、ELCH、Toro、SPA
SLAM方法:ICP、BMICP、IDC、likehood Field、NDT
3、三维重建
泊松重建、Delaunay triangulations、表面重建,人体重建,建筑物重建,树木重建。
实时重建:重建植被或者农作物的4D(3D+时间)生长态势;人体姿势识别;表情识别
4、点云数据管理:点云压缩、点云索引(KD、Octree),点云LOD(金字塔),海量点云的渲染
Spin image
Spin image是基于点云空间分布最经典的特征描述方法。
Spin image的思想是将一定区域的点云分布转换成二维的spin image,然后对场景和模型的spin image进行相似性度量
生成spin image的步骤
1、定义一个Oriented point
2、以Oriented point为轴生成一个圆柱坐标系
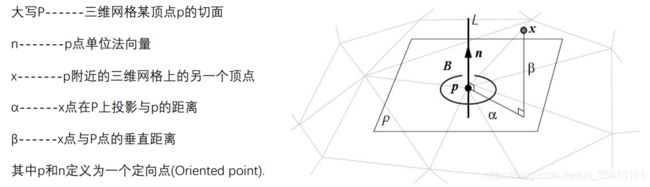
3、定义spin image的参数,spin image是一个具有一定大小(行数列数)、分辨率(二维网格大小)的二维图像(或者说网格)。
spin image的三个关键参数
a、分辨率,即二维网格的也就是像素的实际尺寸,使用和三维网格相近的尺寸比较合适,因此通常取三维网格所有边的平均值来做为spin image的每个网格尺寸,通常会把网格的长和宽定义成相等,即边长。边长的计算公式(e为三维网格模型中的一条边,N为三维网格模型中的边的总数。): r = 1 N ∑ i = 1 N ∣ e i ∣ r=\frac1N\sum_{i=1}^N\left|e_i\right| r=N1i=1∑N∣ei∣b、大小,即spin image的行数和列数,两者一般也相等。可以参考的大小为10x10或20x20等。
c、suppot angle,即法向量夹角的大小限制。空间中顶点的法向量与常见圆柱坐标系所选点法向量之间的夹角。

可以看出,对角度限制以后,那些相当于切面的“凹点(大于90°)”被剔除,保留了主要信息,降低了后续的计算量。一般角度限制范围为60°~90°之间。
4、将圆柱体内的三维坐标投影到二维Spin image,这一过程可以理解为一个spin image绕着法向量n旋转360度,spin image扫到的三维空间的点会落到spin image的网格汇总。
从三维空间投影到spin image坐标:

5、根据spin image中的每个落入的点不同,计算每个网格的强度I.
显示spin image时以每个网格(也就是像素)I不同为依据。最直接的方法是直接计算每个网格中落入的点,然而为了降低对位置的敏感度减低噪音影响增加稳定性,Johnson论文中用双线性插值的方法降一个点分布到4个像素中。
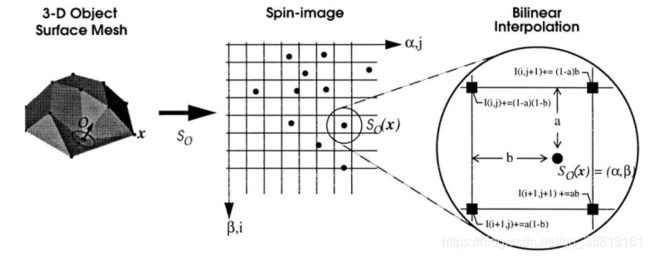
当一个点落入网格 ( i , j ) (i,j) (i,j)中时会被双线性插值分散到 ( i , j ) (i,j) (i,j)、 ( i , j + 1 ) (i,j+1) (i,j+1)、 ( i + 1 , j ) (i+1,j) (i+1,j)、 ( i + 1 , j + 1 ) (i+1,j+1) (i+1,j+1)四个网格中。
binsize b,图像尺寸W

这样就获得了spin image

点云滤波
点云滤波是点云处理的基本步骤,也是进行high level三维图像处理之前必须要进行的预处理。其作用类似于信号处理中的滤波,但实现手段却和信号处理不一样,原因有以下几个方面:
1、点云不是函数,对于复杂三维外形其x,y,z之间并非以某种规律或某种数值关系定义。所以点云无法建立横纵坐标之间的关系。
2、点云在空间中是离散的。和图像,信号不一样,并不定义在某个区域上,无法以某种模板的形式对其进行滤波。换言之,点云没有图像与信号那么明显的定义域。
3、点云在空间中分布很广泛。遍历整个点云中的每个点,并建立点与点之间相互位置关系成了最大难点。不像图像与信号,可以有迹可循。
4、点云滤波依赖于几何信息,而不是数值关系。
5、综上所述,点云滤波只在抽象意义上与信号、图像滤波方式类似。因为滤波的功能都是突出需要的信息。
三维重建
三维重建包括三个房间,基于SFM的运动恢复结构,基于Deep Learning的深度估计和结构重建,以及基于RGB-D深度摄像头的三维重建。
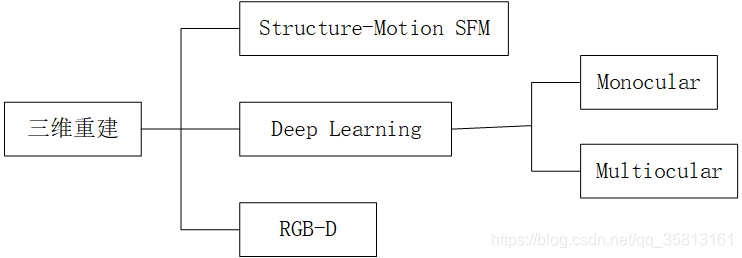
SFM(stucture from Motion),主要基于多视觉几何原理,用于从运动中实现3D重建,也就是从无时间序列的2D图像中推算三维信息,是计算机视觉学科的重要分支。广泛应用于AR/VR,自动驾驶等领域。虽然SFM主要基于多视觉几何原理,随着CNN的在二维图像的积累,很多基于CNN的2D深度估计取得一定效果,用CNN探索三维重建也是不断深入的话题。
深度学习方法呈现上升趋势,但是传统基于多视几何方法热情不减,实际应用以多视几何为主,深度学习的方法离使用还有一段距离。

SfM与三维重建
从二维图像中恢复三维场景结构是计算机视觉的基本任务,广泛应用于3D导航、3D打印、虚拟游戏等。
Structure from Motion(SFM)是一个估计相机参数及三维点位置的问题。
一个基本的SfM pipeline可以描述为:
1、对每张2为图片检测特征点(feature point),对每对图片中的特征点进行匹配,值保留满足几何约束的匹配。
2、执行一个迭代式的、鲁棒的SfM方法来恢复摄像机的内参(intrinisc parameter)和外参(extrinsic parameter)。
3、并由三角化得到三维点坐标。

根据SfM过程中图像添加顺序的拓扑结构,SfM方法可以分为:
- 增量式(incremental/sequential SfM)
- 全局式(Global SfM)
- 混合式(hybrid SfM)
- 层次式(hierarchica SfM)
- 基于语义的SfM(Semantic SfM)
- 基于Deep Learning的SfM
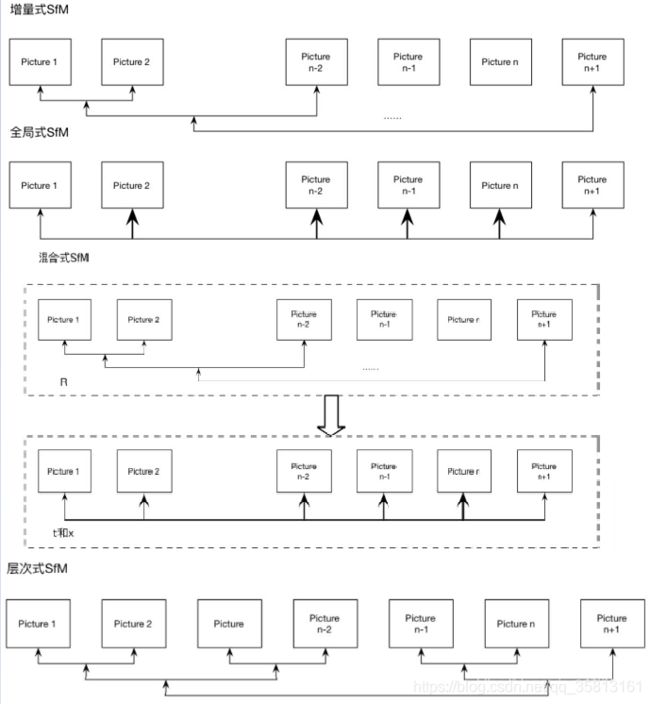
增量式SfM
增量式SfM首先使用SIFT热证检测器提取特征点并计算特征点对应的描述子(descriptor),然后使用ANN(approximate neare neighbor)方法进行匹配,低于某个匹配数阈值的匹配对将会被移除。对于保留下来的匹配对,使用RANSAC(Random Sample Consensus)来估计基本矩阵(fundamental matrix),在估计基本矩阵是被判定为外电(outlier)的匹配被看做是错误的匹配而被移除。对于满足以上几何约束的匹配点,江北合并为tracks。然后通过incremental方式的SfM方法来恢复场景结构。首先需要选择一对好的初始匹配对,一堆好的初始匹配对应该满足:
1、足够多的匹配点
2、宽基线。之后增量式地增加摄像机,估计摄像机的内外参数并由三角化得到三维坐标,然后使用Bundle Adjustment进行优化。
增量式SfM从无序图形几何计算三维重建的常用方法。增量式SfM可分为几个阶段:图像特征提取、特征匹配、几何约束、重建初始化、图像注册、三角化、outlier过滤、Bundle adjustment等步骤。

增量式SfM优势:
1、系统对于特征匹配以及外极几何关系的外点比较鲁棒,重建场景进度高;
2、标定过程通过RANSAC不断过滤外电;
3、捆绑调整地优化场景结构
增量式SfM缺点
1、对初始图像的选择及摄像机的添加顺序敏感;
2、场景漂移,大场景重建的累计误差
3、效率不足,反复的捆绑调整需要大量的计算时间。
全局式SfM
全局式:估计所有摄像机的旋转矩阵和位置并三角化初始场景点。
优势:
1、将误差均匀分布在外极几何图上,没有累计误差。
2、不需要考虑初始图像和图像添加顺序的问题
3、仅执行一次捆绑调整,重建效率高
缺点:
1、鲁棒性不足,旋转矩阵求解时L1范数对外点相对鲁棒,而摄像机位置求解时相对于平移关系对匹配外点比较敏感。
2、场景完整性,过滤外极几何边,可能丢失部分图像。
混合式SfM
混合式SfM在一定出镀上综合了增量式和全局式SfM各自的优点。
混合式SfM的整个pipline可以概括为:
全局估计摄像机旋转矩阵,增量估计摄像机位置,三角化初始场景。

SfM的劣势
1、尽管SfM在计算机视觉取得显著成果并应用,但是大多数SfM基于周围环境是静止这一假设,即相机是运动的,但目标是静止的。当面对移动物体时,整个系统重建效果显著降低。
2、传统SfM基于目标位刚体的假设。
OpenMVG
OpenMVG(Open Multiple View Geometry):开源多视角立体几何库,这是一个cv界处理多视角立体几何的著名开源库,信奉简单、可维护,提供了一套强大的借口,每个模块都被测试过,尽力提供一致可靠的体验。
OpenMVG实现以下典型应用:
1、解决多视角立体几何的精准匹配问题
2、提供一系列SfM需要用到的特征提取和匹配方法;
3、完整的SfM工具链(矫正、参估、重建,表面处理等);
4、openMVG提供可读性强的代码,方便开发者二次开发,核心功能比较精简,所以可以利用它来完善自己的系统。
github地址:http://github.com/openMVG/openMVG
- 从git克隆openMVG到本地(支持windows、linux、mac环境),安装必要的依赖库(缺少依赖库时cmake或make会报错,根据提示安装)。
$ git clone – recursive http://github.com/openMVG/openMVG.git
$ mkdir openMVG_Build
$ cd openMVG Build
$ cmake -DCMAKE_BUILD_TYPE=RELEASE -DOpenMVG_BUILD_TESTS=ON -DOpenMVG_BUILD_EXAMPLES=ON. …/openMVG/src/
$ make
$ make test - CMVS-PMVS(amodified version):将运动结构(SfM)软件的输出作为输入,然后将输入图像分解成一组可管理大小的图像簇。MVS软件可以用来独立和并行地处理每个簇,起哄来自所有簇的重建不错过任何细节。
- Github地址:http://github.com/pmoulon/CMVS-PMVS
- 编译时,切换到克隆远吗目录(build/main文件夹中生成cmvs、genOption、pmvs2三个可执行文件。):
$ mkdir build && cd build
$ cmake …
$ make - 切换到openMVG_Build/software/SfM文件夹中,在终端运行$ python tutorial_demo.py
- 切换到tutorial_out/reconstruction_gloabal目录:$ pmvs2 ./PMVS/ pmvs_options.txt
PMVS/moodels文件夹中生成一个大小为15.2MB的pmvs_options_txt.ply点云文件,用meshlab打开即可看到重建出来的彩色稠密点云: