leetcode 33. 搜索旋转排序数组【图示法解释】

看到logn，想都不用想，肯定二分法。但是“无序数组”二分法怎么用了？

自己想了好久没想出来，看了别人的解释大概懂了：【个人比较喜欢画图，用图解释比较形象】

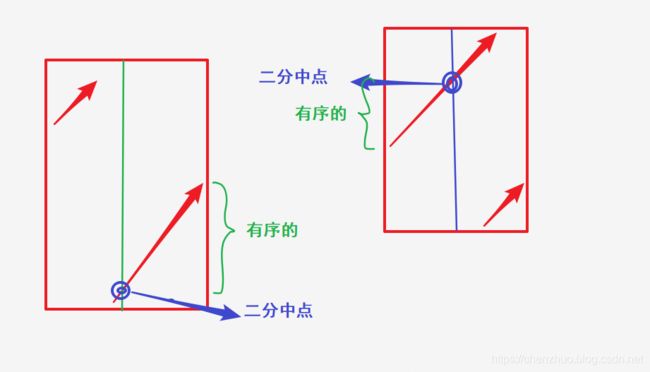
可以看到，尽管是“无序”，但二分的时候左右两边必定有一边是有序的（五五开的情况我没有画进来，那种情况必定有序）。

每次进行二分之后也是如此。

同时，哪一边有序可以通过收尾的大小比较判断 ：

中点小于最右端，则右端有序；

中点大于最右端，则左端有序；

所以根据查找值与有序一方端点值的比较，可知查找值属于哪一边。依次类推。

 

执行用时 : 12 ms, 在Search in Rotated Sorted Array的C++提交中击败了67.22% 的用户

内存消耗 : 9.1 MB, 在Search in Rotated Sorted Array的C++提交中击败了71.47% 的用户

class Solution {
public:
    int search(vector& nums, int target) {
        return bs(nums,0,nums.size()-1,target);
    }
    int bs(vector& nums,int i,int j,int &target)
    {
        if(i>j) return -1;
        int k=(i+j)/2;
        if(nums[k]==target) return k;
        if(nums[k]nums[j]) return bs(nums,i,k-1,target);//不在有序的范围内
            else return bs(nums,k+1,j,target);
        }
        else//左端增序
        {
            if(target>nums[k]||target

细节注意一下：

能用且的地方不用或。因为且有短路操作！！！！！可以加速判断

执行用时 : 4 ms, 在Search in Rotated Sorted Array的C++提交中击败了98.32% 的用户

内存消耗 : 9 MB, 在Search in Rotated Sorted Array的C++提交中击败了71.54% 的用户

class Solution {
public:
    int search(vector& nums, int target) {
        return bs(nums,0,nums.size()-1,target);
    }
    int bs(vector& nums,int i,int j,int &target)
    {
        if(i>j) return -1;
        int k=(i+j)/2;
        if(nums[k]==target) return k;
        if(nums[k]<=nums[j])//右端增序
        {
            if(target>nums[k]&&target<=nums[j]) return bs(nums,k+1,j,target);//在有序的范围内
            else return bs(nums,i,k-1,target);
        }
        else//左端增序
        {
            if(target=nums[i]) return bs(nums,i,k-1,target) ;
            else return bs(nums,k+1,j,target);
        }
    }
};