Python（22）：用SciPy做优化

基本优化问题Demo

和所有的计算机处理问题一样，scipy的optimize其输入也必须规范化。没有规矩，不成方圆。

约束条件

等式类型 g(x) = 0

不等式类型 h(x) >= 0

import numpy as np
import scipy.optimize as sco

def fun_linear(x,flag):
    return (x[0] + 2*x[1])*flag

cons = ({'type':'ineq', 'fun':lambda x: -x[0]+2},
        {'type':'ineq', 'fun':lambda x: -x[1]+2},
        {'type':'ineq', 'fun':lambda x:  x[0]+x[1]-2}
       )
flags = [-1,1]
for flag in flags:
    opt = sco.minimize(fun=fun_linear,x0=[1,1],args=(flag,),constraints=cons)
    print(opt['fun']*flag)

6.0

1.99999999999992

都出这个结果了，那我不得不选A了。

求f的最大值相当于求-f的最小值

房子应该租在哪里

百度经验上有这么一道题。

我找到了一份实习，于是想租一个房子，最好离工作近点，但是还没毕业，学校时不时有事，还不能离学校远了；而且有时候还要去女朋友那里，她希望我就住在她附近，于是，我怎么选择房子的地址？
假定公司、学校、女盆友的在地图上的坐标分别是（x1,y1），（x2,y2），（x3,y3）。
求我的房子的坐标。

## 如果预算有限？
约束条件：只能在五环附近租房
1. 五环是个“环”。半径大概10。
2. 五环是个“方”。点到线段的距离大概是8。

先引入scipy的optimize

import scipy.optimize as sco

最朴实的距离之和最小

# 生成坐标点
p1 = np.array([-1,-2])
p2 = np.array([2,2])
p3 = np.array([-3,2])

cordinates = [p1,p2,p3]

画图的函数

def plot_result(opt, bonds=None):
    
    fig = plt.figure(1,figsize=(6,6))
    
    if bonds == None:
        pass
    else:
        xs,ys = bonds[0],bonds[1]
        plt.plot(xs,ys)
        
    offset = 1.01
    x,y = (opt['x'][0],opt['x'][1])
    plt.scatter(x,y)
    plt.text(x*offset,y*offset,'家')
    labels = ['公司','学校','女友']
    for i in range(len(cordinates)):
        c = cordinates[i]
        plt.scatter(c[0],c[1])
        plt.arrow(x,y, c[0]-x, c[1]-y) # 四个参数分别代表 x,y,dx,dy
        plt.text(c[0]*offset,c[1]*offset,labels[i])
        plt.text((x+c[0])/2*offset,(y+c[1])/2*offset,'距离：%.2f'%(np.sqrt(sum((opt['x']-c)**2))))
    plt.scatter(0,0)
    plt.text(0,0,'市中心')
    plt.title('我的家应该在(%.2f,%.2f)，总距离：%.2f'%(x,y,opt['fun']))
    plt.show()

目标函数

# 等权重的距离之和
# 可以考虑在概率意义下的距离之和最短
def calc_total_dist(x, cordinates):
    total_dist = 0
    for c in cordinates:
        tmp = x - c
        total_dist += np.sqrt(tmp.dot(tmp))
    return total_dist

求最优解

# 求最优解
opt = sco.minimize(fun=calc_total_dist,x0=np.array([0,0]),args=(cordinates))
print(opt)
plot_result(opt)

关于后面几个有约束的问题

添加约束条件就OK

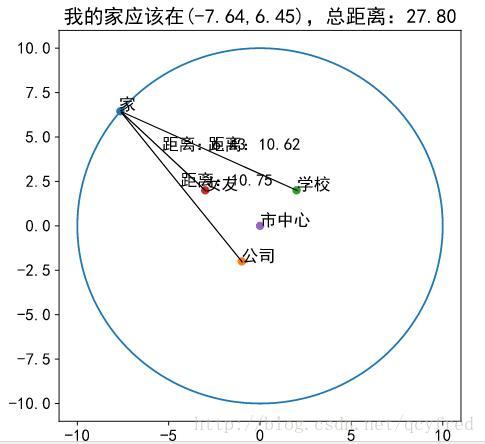
# 求最优解
cons = ({'type':'eq', 'fun': lambda x: x[0]**2 + x[1]**2 - 100})
opt = sco.minimize(fun=calc_total_dist,x0=np.array([10,10]),args=(cordinates),constraints=cons)
print(opt)

# 画出一个环
# 参数方程
t = np.arange(-math.pi, math.pi, 1e-4)
R = 10
xs = 10 * np.cos(t)
ys = 10 * np.sin(t)
bonds = [xs, ys]

plot_result(opt,bonds)

其中，生成边界的时候，用到了曲线的参数方程。

当“五环”不是一个环，而是一个方

这个问题困扰了我一会儿。原因是，一个正方形的曲线的约束方程不好写！

把复杂问题拆成一些简单的问题。4条边不好写，那就在每条边上找一个局部最优解，再在4个局部最优解中找出一个全局最优解。

R = 8

param1 = [0,  1]
param2 = [R, -R]

opt_ress = {}

for k1 in param1:
    for k2 in param2:
        
        # 求每条边上的最优解
        cons = ({'type':'eq', 'fun': lambda x: x[k1] - k2}#,
        #{'type':'eq', 'fun': lambda x: x[1] - R},
        #{'type':'eq', 'fun': lambda x: x[0] + R},
        #{'type':'eq', 'fun': lambda x: x[1] + R}
       )
        opt = sco.minimize(fun=calc_total_dist,x0=np.array([0,0]),args=(cordinates),constraints=cons)
#         print(opt)
        item = {}
        item['fun'] = opt['fun']
        item['opt'] = opt
        opt_ress[(k1,k2)] = item

# print(opt_ress)

min_fun = 1e6
for k,v in opt_ress.items():
    opt['fun'] = opt_ress[k]['fun']
    if min_fun > opt['fun']:
        min_fun = opt['fun']
        min_key = k
        
opt_res = opt_ress[min_key]
home_cord = opt_res['opt']

x1s = np.array([-8,-8,-8,8,8,8,8,-8])
y1s = np.array([-8,8,-8,-8,-8,8,8,8])

bonds = [x1s, y1s]

plot_result(home_cord,bonds)

# min([每条边上的最小的距离])
# 分解复杂问题！！！


# 对numpy.append()和numpy.concatenate()两个函数的运行时间进行比较
# 拼接 np.array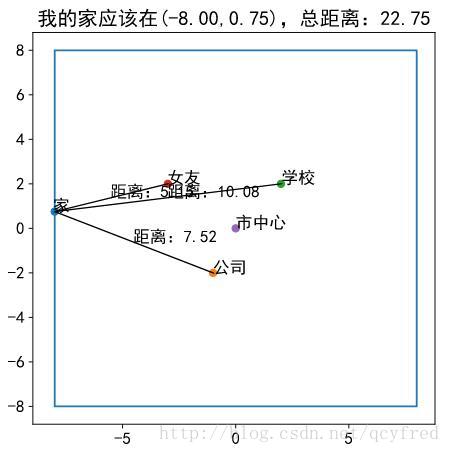

关于绘图，画这个四方形，一条边一条边地画，绕一圈画出来，不然可能会出问题。可能对角线都会被连起来……