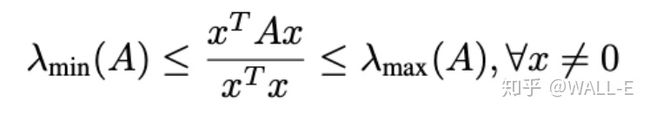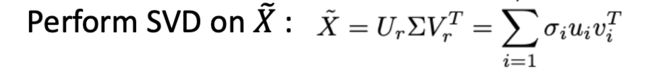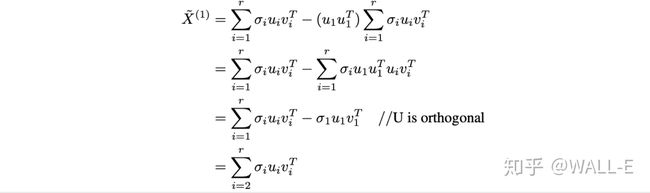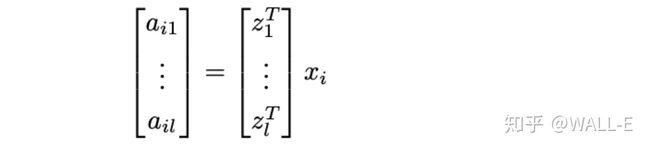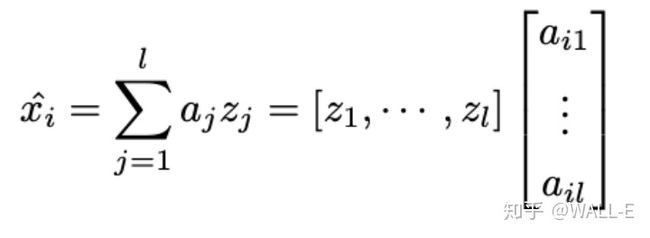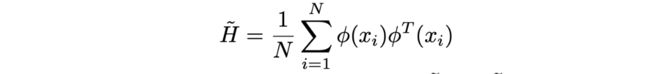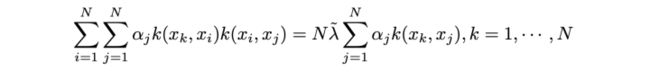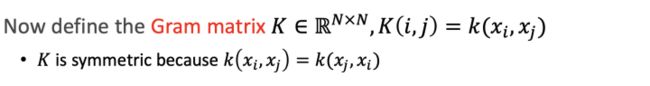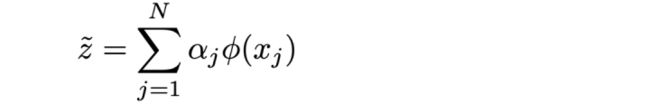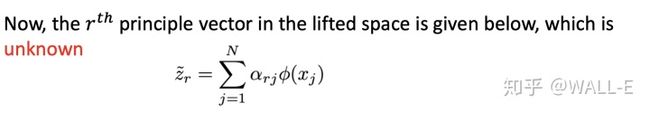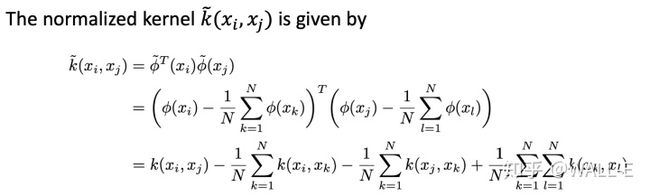三维叉乘怎么算_《三维点云处理》学习笔记（1）：平面法向量估计

一、前言

《三维点云处理》学习笔记系列文章是我在学习深蓝学院的这门课时做的笔记，其中很多截图都来自于老师的ppt。主要目的是记录和备忘，以及分享和交流。

code:https://github.com/QinZiwen/analyze_pointcloud

---

二、什么是三维点云

2.1 定义

三维点云（point cloud）就是很多点的统称（^_^），当然这里点可以是普通意义上的点，即三维向量，表示点在三维坐标系中的位置；也可以是广义上的点，可能是一个N纬的向量，其中包含点的三维位置，颜色，语义信息等等，笼统的可以认为是三维位置加其他属性。这些其他属性有的可以从传感器中直接获取，有的则需要点云数据分析后得到。为了简单起见，我们从最简单的三维点云开始（后面简称点云），即每个点由他的三维位置表示。那么很多点就可以用3 * N矩阵表示，或者N * 3的矩阵表示，如下图左边所示，右边就是广义的情况。

2.2 点云的来源

点云的来源有很多：激光雷达，深度摄像头，CAD模型，SLAM/SFM

2.3 点云的应用

在机器人和自动驾驶领域：定位（包括3DoF，6DoF的定位），场景描述等

在消费电子领域：Face ID，hololens的hand pose， human pose等

2.4 点云的优缺点

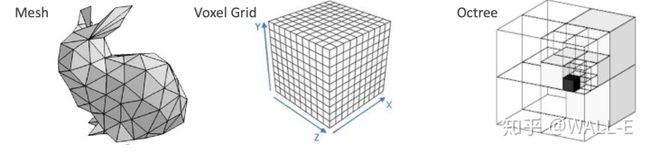
点云可以看做是空间的一种表达，除此之外，空间还可以使用mesh，voxel grid，octree表示。

点云相比于其他表达而言，优点是简单，不仅理解起来简单，而且数学表示上也非常简单。缺点也很明显，具有稀疏性，平移和旋转不变性，无序性等。

---

三、PCA（Principle Component Analysis）

PCA在点云预处理，平面检测，法向量求解等中都有应用，我之前还有见过用PCA对点云中的点分类，地面点，墙面点，物体上的点等，然后再做其他处理。所以我们就从PCA的推导开始，在开始之前，我们先介绍两个定理，会在PCA的证明中用到。

第一个是谱定理，大致意思是对于一个对称矩阵，我们可以用他的特征值特征向量的线性组合表示，严格说明如下：

第二个是瑞利熵（瑞利熵和广义瑞利熵_人工智能_wyl1813240346的博客-CSDN博客）

下面介绍PCA，他的输入输出是：

和线性代数中一样，我们默认是列向量。

PCA叫主成分分析，那么什么是主成分（或主方向）？数据在该方向上的方差最大。从主方向的定义上就可以看出PCA和方差有千丝万缕的联系，在下面的证明过程中，我们可以留意一下。

首先，对输入数据去均值：

屏蔽向量中的具体数字对计算的影响，去除均值之后，留下可以理解为数据的分布特征，只不过他依然蕴含在所有的向量中。

PCA希望寻找一个方向（主方向），使得数据在该方向上的方差最大，我们假设一个主方向

，然后投影到该方向上，即内积：

由于数据已经减去了均值，那么根据方差的定义，平方求和就是方差了：

我们的目标是方差最大，所以：

注意：这个式子求解的变量是

。

在这里，

是对称阵，还记得瑞利熵吗？

他告诉了我们对称阵两边乘上向量后的上下界，由于

是单位向量，上式和我们的目标函数一毛一样。即，当

取

的最大特征值对应的特征向量时，我们的目标函数取到最大值。

怎么得到特征值特征向量呢？当然是SVD喽（SVD（奇异值分解）小结 - EndlessCoding - 博客园），对

进行SVD分解：

那么：

如果特征值由大到小排列，那么

的第一列就是最大特征值对应的特征向量。至此，我们找到了一个主方向，数据在这个方向上投影后，方差最大。那么我们想知道投影后方差次大的方向（

），该怎么求解？

大致思路是：从原数据中减掉原数据在主防线上的投影向量后，在按照上面方法求特征向量。

在这里

，即最大特征值对应的特征向量。

表示

在主方向上的投影长度，然后在左乘

表示

投影到主方向上的向量，我们将这个向量从

中减掉，得到

。

上式相当于得到了

的SVD分解，即，我们从原数据上减掉了主方向上的分量，那么，新的得到的数据的SVD分解中刚好是之前SVD分解不包含最大特征值和特征向量的样子。

当我们再去求方差最大时对应的向量时，可以发现，正式原始数据的第二大特征向量，至此我们得到了

。以此类推，我们可求

等等。

总结一下PCA算法：

1）去中心：

2）求协方差矩阵：

3）对

进行SVD分解，并且特征向量按照由大小排列。

4）主要方向就是

中的列向量。

---

四、PCA的应用之一

注意：

将原始数据进行压缩（降维）：

解压（升维），就是等式两边同时乘上特征向量组成举证的转置（因为是正交阵，所以逆和转置相等）：

---

五、核PCA（Kernel PCA）

5.1 核PCA推导

传统PCA本质上是线性的，我们可以回想不管是PCA推到过程还是PCA的应用例子，其中基本应用的都是矩阵乘法，矩阵乘法本质上是一只中线性变换。

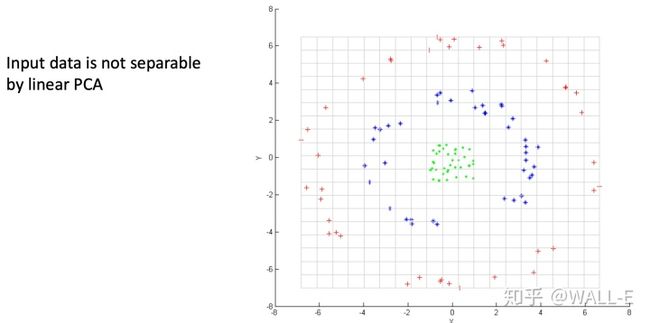
如下图所示，绿色和红色各表示一类数据，我们想找到一个主方向，将数据投影后，可以用直线将两类点分开。但是在二维空间上我们很难找到这一个主方向。

假设上图中的数据为：

我们设计一个函数：

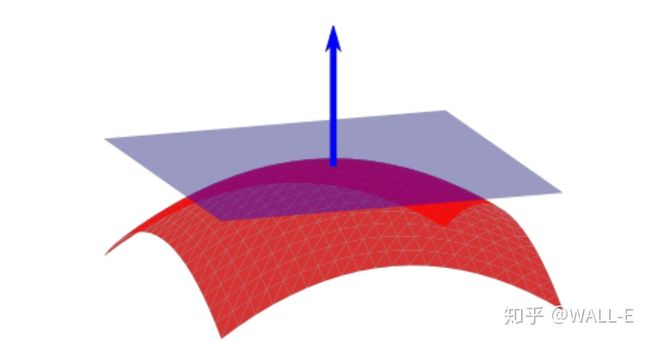
可以将原来二维数据升到三维数据，如下图所示，当然这个函数，你可以设计成各种各样：

此时，我们发现绿色和红色点线性可分了。

我们套用前面介绍的PCA算法：

1）使用

函数将原始数据升维，并且假设均值为零，即：

2）计算协方差矩阵：

3）求

的特征值特征向量。

不知道你有没有注意到，

会是一个高纬矩阵，有时候维度可能非常高，比如将一帧1280*720的图像向量化后，再使用

升维，可想而知，维度会非常高，处理起来比较麻烦。

下面我们来推到核PCA，看看他是怎么解决这个问题。

根据特征值特征向量的定义：

其中：

是特征向量，

是特征值。

将

带入到上述定义中：

发现等式左边除了

是向量外，其他都是标量，那我们就可以把他们合并到一起：

这个式子在说，特征向量是输入数据的线性组合。其实这个也可以直观理解，原来的PCA也就是把数据旋转平移缩放后，找到了一些主方向。

在这里我们定义一个核函数

带入上式

等式两边同乘

定义一个gram矩阵（Gram矩阵_人工智能_wangyang20170901的博客-CSDN博客）：

整理上式，得：

我们稍微回头看一下，上面这一堆做了什么工作。因为

可以表示成输入数据的线性组合，这里求得的

正是组合系数。

好事往往多磨，组合后我们还得保证

是单位向量，很简单，我们就单位化一下呗。

用

替换掉等式右边的

，得：

。

也就说为了单位化

，我们需要

为什么说上式，依然没有办法求解，因为

函数我们还没有定义。但是怎么定义呢？不知道呀，这是个玄学问题，看看数学家是怎么解决的。

我们想一下，这里求主方向的目的是什么？其中一个很重要的原因是为了把数据投影到主方向上。那我们就先把数据投影到

，然后看看会发生什么：

哎，核函数又出现，也就说说如果我们可以求出这个核函数，那么问题就得解了，因为不用管

的定义，我就可以计算出投影后的向量了。那么怎么求这个核函数的值呢？当然是按照他的定义展开了，但是：

那就去中心化喽：

接着：

对于所有数据我们可以写一个核矩阵：

所有的矛头都指向了核函数，下面介绍几种常用的核函数。

5.2 核函数

5.3 核PCA算法

5.4 核PCA的例子

5.5 核PCA的讨论

1）核函数是得我们避免显式计算高纬向量。

2）核PCA是得我们突破了输入数据空间的限制。

---

六、PCA在点云中的应用

6.1 平面法向量估计

思想：找一堆点最小特征值对应的特征向量。

6.2 平面发向量算法

6.3 如何处理噪声

---

参考：

[1] 常用数学符号的 LaTeX 表示方法: http://www.mohu.org/info/symbols/symbols.htm