蚁狮优化算法( Ant Lion Optimizer,ALO)-Matlab源码
![]()
获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 蚁狮优化器Ant Lion Optimizer (ALO)
-
- 启发
- ALO算子
-
- 随机游走
- 困于蚁狮坑
- 构造陷阱
- 蚂蚁滑向蚁狮
- 捕捉猎物和重建坑
- 精英
- ALO算法
蚁狮优化器Ant Lion Optimizer (ALO)
2015年,Seyedali Mirjalili提出了一种新型的受自然启发的算法——蚁狮优化算法(Ant Lion Optimizer ,ALO),该算法模模仿了自然界中蚁狮在捕猎蚂蚁时的智能行为。关注公众号后发送“蚁狮”或“ALO”获取Matlab源码下载链接!
启发
蚁狮属于蚁蛉科,为脉翅目类昆虫。蚁狮的生命周期包括两个主要阶段:幼虫和成虫,自然总寿命可达3年,主要发生在幼虫(成年期为3-5周)。
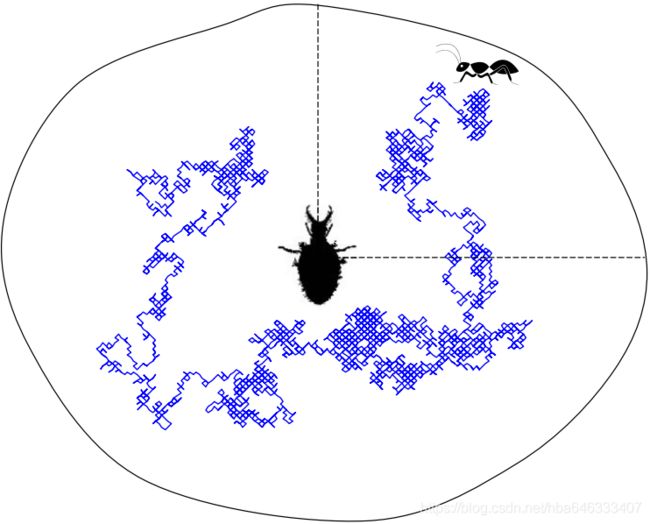
它们的名字源于它们独特的捕猎行为和它们最喜爱的猎物。一只蚁狮幼虫沿着一条圆形的路径在沙子里挖出一个圆锥形的坑,并用它巨大的下颚把沙子扔出去。图1(a)显示了几个不同大小的锥状坑。挖好陷阱后,幼虫藏在圆锥体的底部(作为一个坐等捕食者),等待昆虫(最好是蚂蚁)被困在坑里,如拖1(b)所示。锥的边缘很急剧,昆虫可以很容易地掉到陷阱的底部。一旦蚁狮意识到猎物在陷阱里,它就会试图抓住它。然而,昆虫通常不会立即被捕捉,它们会试图逃离陷阱。在这种情况下,蚁群会聪明地将沙子扔向洞穴边缘,将猎物滑入洞穴底部。当猎物被抓住时,它会被拉到土壤下面被吃掉。吃掉猎物后,蚁狮会把剩下的猎物扔到坑外,并修复坑为下次捕猎做准备。
另一个观察到的关于蚁狮生活方式的有趣行为是陷阱的大小和两件事的相关性:饥饿程度和月亮形状。当蚁狮感到饥饿或者月圆时,往往会挖出更大的陷阱。它们已经进化并适应了这种方式来提高它们的生存机会。人们还发现,安狮子不会直接通过观察月亮的形状来决定陷阱的大小,但它有一个内部的月球时钟来做出这样的决定。
ALO算子
ALO算法模拟了蚁狮和陷阱中的蚂蚁之间的交互,为了模拟这种交互作用,蚂蚁需要在搜索空间中移动,而蚁狮则可以捕猎它们。由于蚂蚁在自然界中寻找食物时是随机移动的,因此通过选择一个随机行走来模拟蚂蚁的运动:
X ( t ) = [ 0 , cumsum ( 2 r ( t 1 ) − 1 ) , cumsum ( 2 r ( t 2 ) − 1 ) , … , cumsum ( 2 r ( t n ) − 1 ) ] (1) X(t)=\left[0, \text { cumsum }\left(2 r\left(t_{1}\right)-1\right), \text { cumsum }\left(2 r\left(t_{2}\right)-1\right), \ldots, \text { cumsum }\left(2 r\left(t_{n}\right)-1\right)\right]\tag{1} X(t)=[0, cumsum (2r(t1)−1), cumsum (2r(t2)−1),…, cumsum (2r(tn)−1)](1)
其中 cumsum \text {cumsum} cumsum计算了累积和, n n n为最大迭代次数, t t t表示随机游走的步数(即迭代), r ( t ) r(t) r(t)通过以下定义的随机函数:
r ( t ) = { 1 if rand > 0.5 0 if rand ⩽ 0.5 (2) r(t)=\left\{\begin{array}{ll} 1 & \text { if rand }>0.5 \\ 0 & \text { if rand } \leqslant 0.5 \end{array}\right.\tag{2} r(t)={ 10 if rand >0.5 if rand ⩽0.5(2)
其中 r a n d rand rand为[0,1]内服从均匀分布的随机数。
在优化过程中将蚂蚁的位置保存至以下矩阵中:
M A n t = [ A 1 , 1 A 1 , 2 … … A 1 , d A 2 , 1 A 2 , 2 … … A 2 , d : : : : ⋮ : ⋮ : : ⋮ A n , 1 A n , 2 … … A n , d ] (3) M_{A n t}=\left[\begin{array}{ccccc} A_{1,1} & A_{1,2} & \ldots & \ldots & A_{1, d} \\ A_{2,1} & A_{2,2} & \ldots & \ldots & A_{2, d} \\ : & : & : & : & \vdots \\ : & \vdots & : & : & \vdots \\ A_{n, 1} & A_{n, 2} & \ldots & \ldots & A_{n, d} \end{array}\right]\tag{3} MAnt=⎣⎢⎢⎢⎢⎢⎢⎡A1,1A2,1::An,1A1,2A2,2:⋮An,2……::………::…A1,dA2,d⋮⋮An,d⎦⎥⎥⎥⎥⎥⎥⎤(3)
其中 M A n t M_{A n t} MAnt为用于存储每只蚂蚁位置的矩阵, A i , j A_{i,j} Ai,j为第 i i i只蚂蚁的第 j j j个变量(维度)的值, n n n为蚂蚁数量, d d d为变量个数。这里的蚂蚁有点类似于PSO中的粒子,矩阵 M A n t M_{A n t} MAnt中保存了所有蚂蚁的位置(所有解的变量)。
采用如下的适应度函数评估每只蚂蚁的目标值:
M O A = [ f ( [ A 1 , 1 , A 1 , 2 , … , A 1 , d ] ) f ( [ A 2 , 1 , A 2 , 2 , … , A 2 , d ] ) ⋮ ⋮ f ( [ A n , 1 , A n , 2 , … , A n , d ] ) ] (4) M_{O A}=\left[\begin{array}{c} f\left(\left[A_{1,1}, A_{1,2}, \ldots, A_{1, d}\right]\right) \\ f\left(\left[A_{2,1}, A_{2,2}, \ldots, A_{2, d}\right]\right) \\ \vdots \\ \vdots \\ f\left(\left[A_{n, 1}, A_{n, 2}, \ldots, A_{n, d}\right]\right) \end{array}\right]\tag{4} MOA=⎣⎢⎢⎢⎢⎢⎢⎡f([A1,1,A1,2,…,A1,d])f([A2,1,A2,2,…,A2,d])⋮⋮f([An,1,An,2,…,An,d])⎦⎥⎥⎥⎥⎥⎥⎤(4)
其中 M O A M_{O A} MOA中保存了每只蚂蚁的适应度值, f f f为目标函数。
除了蚂蚁,我们认为蚁狮也隐藏在搜索空间的某个地方,同样它也有对应的位置矩阵和适应度值矩阵:
M Antlion = [ A L 1 , 1 A L 1 , 2 … … A L 1 , d A L 2 , 1 A L 2 , 2 … … A L 2 , d : : ⋮ : : ⋮ ⋮ ⋮ : ⋮ A L n , 1 A L n , 2 … … A L n , d ] (5) M_{\text {Antlion}}=\left[\begin{array}{ccccc} A L_{1,1} & A L_{1,2} & \ldots & \ldots & A L_{1, d} \\ A L_{2,1} & A L_{2,2} & \ldots & \ldots & A L_{2, d} \\ : & : & \vdots & : & : \\ \vdots & \vdots & \vdots & : & \vdots \\ A L_{n, 1} & A L_{n, 2} & \ldots & \ldots & A L_{n, d} \end{array}\right]\tag{5} MAntlion=⎣⎢⎢⎢⎢⎢⎢⎡AL1,1AL2,1:⋮ALn,1AL1,2AL2,2:⋮ALn,2……⋮⋮………::…AL1,dAL2,d:⋮ALn,d⎦⎥⎥⎥⎥⎥⎥⎤(5)
其中 M Antlion M_{\text {Antlion}} MAntlion为每只蚁狮的位置矩阵, A L i , j A L_{i,j} ALi,j为第 i i i只蚁狮的第 j j j个维度的值, n n n为蚁狮数量, d d d为变量个数(维度)。
M 0 A L = [ f ( [ A L 1 , 1 , A L 1 , 2 , … , A L 1 , d ] ) f ( [ A L 2 , 1 , A L 2 , 2 , … , A L 2 , d ] ) ⋮ ⋮ f ( [ A L n , 1 , A L n , 2 , … , A L n , d ] ) ] (6) M_{0 A L}=\left[\begin{array}{c} f\left(\left[A L_{1,1}, A L_{1,2}, \ldots, A L_{1, d}\right]\right) \\ f\left(\left[A L_{2,1}, A L_{2,2}, \ldots, A L_{2, d}\right]\right) \\ \vdots \\ \vdots \\ f\left(\left[A L_{n, 1}, A L_{n, 2}, \ldots, A L_{n, d}\right]\right) \end{array}\right]\tag{6} M0AL=⎣⎢⎢⎢⎢⎢⎢⎡f([AL1,1,AL1,2,…,AL1,d])f([AL2,1,AL2,2,…,AL2,d])⋮⋮f([ALn,1,ALn,2,…,ALn,d])⎦⎥⎥⎥⎥⎥⎥⎤(6)
M 0 A L M_{0 A L} M0AL为保存每只蚁狮适应度值的矩阵, f f f为目标函数。
优化时需要满足以下条件:
- 蚂蚁使用不同的随机游走在搜索空间中移动。
- 随机游走应用于蚂蚁的所有维数。
- 随机游走受到蚁狮陷阱的影响。
- 蚁狮可以建立与适合度成比例的坑(适合度越高,坑越大)。
- 坑大的蚁狮更容易捉到蚂蚁。
- 每只蚂蚁都可以在每次迭代中被一只蚁狮和精英(最优的蚁狮)捕获。
- 自适应地减小随机游走范围来模拟蚂蚁滑向蚁狮。
- 如果蚂蚁优于蚁狮,这意味着它会被蚁狮抓住并拖到沙子下面。
- 蚁狮会根据最近捕获的猎物重新定位,并筑起一个坑来改善每次捕猎后捕获另一个猎物的变化。
随机游走
随机游走均基于式(1)。蚂蚁在每一步的优化中都通过随机游走来更新它们的位置。但是,由于每个搜索空间都有一个边界(变量范围),式(1)不能直接用于蚂蚁位置的更新。为了使随机游走保持在搜索空间内,使用下式对其进行归一化(最小-最大归一化):
X i t = ( X i t − a i ) × ( d i − c i t ) ( d i t − a i ) + c i (7) X_{i}^{t}=\frac{\left(X_{i}^{t}-a_{i}\right) \times\left(d_{i}-c_{i}^{t}\right)}{\left(d_{i}^{t}-a_{i}\right)}+c_{i}\tag{7} Xit=(dit−ai)(Xit−ai)×(di−cit)+ci(7)
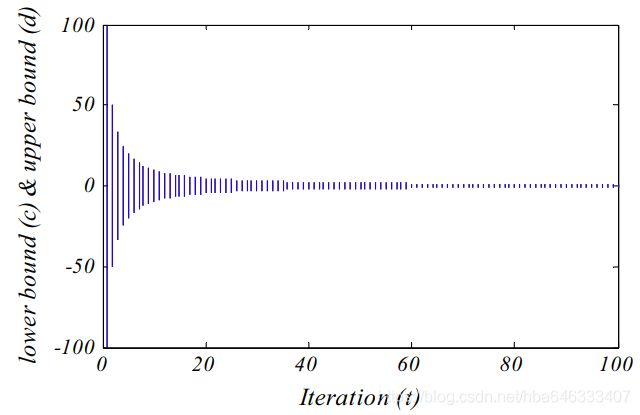
其中 a i a_{i} ai为第 i i i个变量随机游走的最小值, d i d_i di是最大值。 c i t c_{i}^{t} cit是第 t t t次迭代中第 i i i个变量的最小值, d i t d_{i}^{t} dit是第 t t t次迭代中第 i i i个变量的最大值。
在每次迭代中都需要使用式(7),以保证搜索空间内出现随机游走。
困于蚁狮坑
如上所述,蚂蚁的随机游走会受到蚁狮陷阱的影响。为了对这一假设进行数学建模,提出以下方程:
c i t = Antlion j t + c t (8) c_{i}^{t}=\text {Antlion}_{j}^{t}+c^{t}\tag{8} cit=Antlionjt+ct(8)
d i t = Antlion j t + d t (9) d_{i}^{t}=\text {Antlion}_{j}^{t}+d^{t}\tag{9} dit=Antlionjt+dt(9)
其中 c t c^{t} ct为第 t t t次迭代中所有变量的最小值, d t d^{t} dt为第 t t t次迭代中所有变量的最大值, c i t c_{i}^{t} cit为第 i i i只蚂蚁所有变量的最小值, d i t d_{i}^{t} dit为第 i i i只蚂蚁所有变量的最大值, Antlion j t \text {Antlion}_{j}^{t} Antlionjt表示第 t t t次迭代中选择的第 j j j只蚁狮的位置。
式(8)和(9)表达了由向量 c c c和 d d d所定义的超球面中所选择的蚁狮附近的蚂蚁随机游走,如图3所示。
构造陷阱
为了模拟蚁狮的狩猎能力,使用了轮盘赌。如图3所示,假设蚂蚁只被困在一个选定的蚁狮中。ALO算法需要利用轮盘赌算子在优化过程中根据蚁狮的适应度选择蚁狮。这种机制为更适应的蚁狮捕捉蚂蚁提供了很大的机会。
蚂蚁滑向蚁狮
根据目前提出的机制,蚁狮可以根据自身的适合度设置陷阱,而且蚂蚁需要随机移动。然而,一旦蚁狮意识到有一只蚂蚁被困在陷阱里,它们就会把沙子从洞中央往外喷。这种行为可以将试图逃跑的被困蚂蚁滑选。通过自适应地减小蚁群随机游走超球面半径,建立了蚁群随机游走超球面的数学模型:
c t = c t I (10) c^{t}=\frac{c^{t}}{I}\tag{10} ct=Ict(10)
d t = d t I (11) d^{t}=\frac{d^{t}}{I}\tag{11} dt=Idt(11)
其中 I I I为比率,其中 c t c^{t} ct为第 t t t次迭代中所有变量的最小值, d t d^{t} dt为第 t t t次迭代中所有变量的最大值。
在式(10)和(11)中, I = 1 0 w t T I=10^{w} \frac{t}{T} I=10wTt,其中 t t t为当前迭代, T T T为最大迭代次数, w w w是根据当前迭代定义的常量( t > 0.1 T t>0.1T t>0.1T时 w = 2 w=2 w=2, t > 0.5 T t>0.5T t>0.5T时 w = 3 w=3 w=3, t > 0.75 T t>0.75T t>0.75T时 w = 4 w=4 w=4, t > 0.9 T t>0.9T t>0.9T时 w = 5 w=5 w=5, t > 0.95 T t>0.95T t>0.95T时 w = 6 w=6 w=6)。 w w w可以调整利用的精度水平,如图4所示。该方程缩小了蚂蚁位置的更新半径,模拟了蚂蚁在坑内的滑动过程,从而保证了在搜索空间内进行利用。
捕捉猎物和重建坑
捕猎的最后阶段是当一只蚂蚁到达洞穴底部时被蚁狮的下巴夹住。过了这个阶段,蚁狮就把蚂蚁拉进沙子里并吃掉它的身体。为了模拟这个过程,假设当蚂蚁比对应的蚁狮更适应(进入沙子里)时,捕获猎物就会出现。然后,蚁狮需要将自己的位置更新到被猎杀蚂蚁的最新位置,以增加它捕捉新猎物的机会。对此有如下公式:
Antlion j t = A n t i t if f ( A n t i t ) > f ( Antlion j t ) (12) \text { Antlion }_{j}^{t}=A n t_{i}^{t} \quad \text { if } f\left(A n t_{i}^{t}\right)>f\left(\text {Antlion}_{j}^{t}\right)\tag{12} Antlion jt=Antit if f(Antit)>f(Antlionjt)(12)
Antlion j t \text { Antlion }_{j}^{t} Antlion jt表示第 t t t次迭代中第 j j j只蚁狮的位置, Ant i t \text { Ant }_{i}^{t} Ant it表示第 t t t次迭代中第 i i i只蚂蚁的位置
精英
精英主义是进化算法的一个重要特征,它使进化算法能够在优化过程的任何阶段保持获得的最佳解。在本研究中,保存到目前为止在每个迭代中获得的最佳蚁狮,并将其视为一个精英。因为精英是最适合的蚁狮,它应该能够在迭代过程中影响所有蚂蚁的运动。因此,假设每只蚂蚁同时围绕通过轮盘赌随机选择的蚁狮和精英进行随机游走,有如下:
A n t i t = R A t + R E t 2 (13) A n t_{i}^{t}=\frac{R_{A}^{t}+R_{E}^{t}}{2}\tag{13} Antit=2RAt+REt(13)
其中 R A t R_{A}^{t} RAt为在第 t t t次迭代中围绕根据轮盘赌选择的蚁狮的随机游走, R E t R_{E}^{t} REt为在第 t t t次迭代中围绕精英的随机游走, A n t i t A n t_{i}^{t} Antit表示第 t t t次迭代中第 i i i只蚂蚁的位置。
ALO算法
根据上述提出的算子,现在可以定义ALO优化算法。该算法被定义为一个三元组函数,用于逼近优化问题的全局最优,如下所示:
A L O ( A , B , C ) (14) ALO(A,B,C)\tag{14} ALO(A,B,C)(14)
其中 A A A用于生成随机初始解, B B B用于对初始解进行操作,当满足终止条件时 C C C返回true。函数 A , B , C A,B,C A,B,C的定义如下:
∅ ⟶ A { M A n t , M O A , M A n t l i o n , M O A L } (15) \emptyset \stackrel{A}{\longrightarrow}\left\{M_{A n t}, M_{O A}, M_{A n t l i o n}, M_{O A L}\right\}\tag{15} ∅⟶A{ MAnt,MOA,MAntlion,MOAL}(15)
{ M A n t , M A n t l i o n } → B { M A n t , M A n t l i o n } (16) \left\{M_{A n t}, M_{A n t l i o n}\right\} \stackrel{B}{\rightarrow}\left\{M_{A n t}, M_{A n t l i o n}\right\}\tag{16} { MAnt,MAntlion}→B{ MAnt,MAntlion}(16)
{ M A n t , M Antlion } → C { true, false } (17) \left\{M_{A n t}, M_{\text {Antlion}}\right\} \stackrel{C}{\rightarrow}\{\text {true, false}\}\tag{17} { MAnt,MAntlion}→C{ true, false}(17)
ALO算法的伪代码定义如下: