机器学习算法——「Logistic回归」
一、前言
首先,我们要知道,什么是Logistic回归?查阅度娘得到:
Logistic回归又称Logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘、疾病自动诊断和经济预测等领域。
参考:百度百科-Logistic回归
看了上面的定义,有人可能要问了,那什么是广义线性?什么是回归分析呢?
首先,这里的线性是广义的,不是我们通常所说的“狭义线性”。
狭义线性模型(Linear Model): 通常指自变量和因变量之间按比例,成直线的关系。
广义线性模型(Generalized Linear Model,GLM): 线性模型的扩展,主要通过联结函数使预测值落在响应变量的变幅内,如逻辑回归:

什么是回归呢?简单来讲,研究两个变量X与Y之间的统计分析方法的过程就是回归。
其中,我们令X为自变量,Y为因变量。
假设现在有一些数据点,我们利用一条直线对这些点进行拟合(也叫最佳直线拟合),这个拟合的过程就称为回归,如下图所示,当然这只是二维回归,还有多维回归,这里就不详细展开了。

回归的基本思想:根据训练数据和分类边界线方程(方程参数未知),得到最佳拟合参数集,从而实现数据的分类。
通常,Logistic回归适用于二值型输出分类,即二分类,也就是分类结果只有两种情况:是与否,发生与不发生等。
那么,如何得到Logistic回归分类器的最佳拟合参数呢?咱们接着往下看。
二、Sigmod函数
既然,Logistic回归的输出只有两种情况,那么我们有必要引入一种函数,该函数只有两种输出,0或者1。
有人可能会想到单位阶跃函数,没错,确实可以,但是考虑到单位阶跃函数是分段函数,其在x=0处的跳变不方便用代码处理。
故此,我们介绍另外一种函数——Sigmod函数。
其实,从数学的角度上讲,这也是一种阶跃函数。
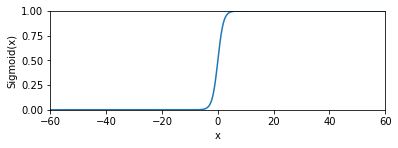
Sigmoid函数也叫Logistic函数,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。
当x=0时,Sigmod(0)的值为0.5。
为了实现分类器,我们将每个样本的每个特征值乘以相应的回归系数,然后求和,并带入Sigmod函数。
当结果大于0.5时,该样本被归为1类;当结果小于0.5时,该样本归为0类。这样我们就实现了Logistic的二分类。
所以,Logistic分类,也是一种概率估计,即样本有多大的概率被划分为某一类。
直观一点,看下图。
这也是最简单的深度神经网络模型。
其中,x可以视为样本的特征值,w是各特征值的回归系数(也是我们要求的最佳拟合系数),f()函数可视为Sigmod函数,阈值就是0.5。

三、梯度下降算法
通过上面介绍的Sigmod函数,我们知道其输入是:
z = w 0 x 0 + w 1 x 1 + w 2 x 2 = w T x z=w_0x_0+w_1x_1+w_2x_2=w^Tx z=w0x0+w1x1+w2x2=wTx
其中,w向量就是我们需要找到的最佳拟合系数,x是样本特征值。
那么,如何找到这组最佳拟合系数呢?换言之,已知一些数据,如何求里面的未知参数,给出一个最优解呢?
线性回归模型中,假设自变量和因变量满足如下形式:
y = h θ ( x ) = θ T x y=h_θ(x)=θ^Tx y=hθ(x)=θTx
通常,我们将参数的求解问题转化为求最小误差问题。 一般采用模型预测结果与真实结果的差的平方和作为损失函数(Loss Function):
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(θ)=\frac{1}{2m} \sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
因此,我们需要找到使损失函数取得最小值时的参数θ。
接下来,怎么找损失函数的最小值呢?这也是求最优解的一个过程,为此我们引入一个最优化算法——梯度下降算法。
梯度下降(Gradient descent )是利用一阶的梯度信息找到函数局部最优解的一种方法,也是机器学习里面常用的一种优化方法。
其基本思想:由于梯度方向是某一个函数值域变化最快的方向,所以要找函数的最值,最好的办法就是沿该函数的梯度方向寻找。
∇ f ( θ ) = ∂ J ( θ ) ∂ θ \nabla f(θ) = \frac{\partial J(θ)}{\partial θ} ∇f(θ)=∂θ∂J(θ)
要找到损失函数的最小值,只需要每一步都往下走,也就是每一步都可以让误差损失函数小一点,无限逼近最小值。
梯度下降算法的迭代公式:
θ j ′ = θ j − α ∂ J ( θ ) ∂ θ j = θ j − 1 m α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) θ_{j}^{'}=\theta_j-\alpha\frac{\partial J(θ)}{\partial θ_j} = \theta_j-\frac{1}{m}\alpha\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj′=θj−α∂θj∂J(θ)=θj−m1αi=1∑m(hθ(x(i))−y(i))xj(i)
其中,α是步长,y(i)是真实值,h(x)是预测值,j表示第j个回归系数,i表示第i个样本。
到这里,我们便得到了梯度下降算法的参数迭代公式。接下来,便是具体的算法编程了。
四、算法编程
Logistic回归的算法编程主要分为以下几个步骤:
1.收集样本数据,并转化成我们需要的格式。
2.建立sigmod函数与最优化函数模型。
3.训练Logistic分类器,得到最优解,并画出最佳拟合曲线(也叫决策边界)。
1.样本数据
这里,我们直接采用《机器学习实战》中给的样本数据集,该数据集的基本格式如下:

其中,第一列和第二列是样本的两个特征值X1和X2,第三列是样本的类别标签。
我们需要将该样本处理成分类器能够识别的格式,同时为了方便矩阵运算(因为有三个回归系数),我们额外引入一个特征值X0,并设置其值为1。
代码如下:
'''
Created on Oct 27, 2010
Logistic Regression Working Module
@author : Peter
@modified by Robert Nie on July 15,2020
'''
def loadDataSet():
dataMat = []; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
# 处理成列表,共100个元素;每个元素也是包含三个特征值的列表
lineArr = line.strip().split()
# 额外加入X0=1这个特征值
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
上面这个函数是数据集加载函数,它将数据集分成了两部分:特征值列表和类别标签列表。处理完以后的部分数据集如下:
[[1.0, -0.017612, 14.053064], [1.0, -1.395634, 4.662541], [1.0, -0.752157, 6.53862], [1.0, -1.322371, 7.152853],...... [1.0, -0.679797, 1.22053], [1.0, 0.677983, 2.556666], [1.0, 0.761349, 10.693862], [1.0, -2.168791, 0.143632], [1.0, 1.38861, 9.341997], [1.0, 0.317029, 14.739025]]
[0, 1, 0, 0,...... , 1, 1, 0, 1, 0, 0]
2. Sigmod函数和梯度下降算法
由前面的分析可知,代码如下:
'''
Created on Oct 27, 2010
Logistic Regression Working Module
@author: Peter
@modified by Robert Nie on July 15,2020
'''
import numpy as np
def sigmoid(inX):
return 1.0/(1+np.exp(-inX))
def gradDecline(dataMatIn, classLabels):
"""
实现梯度下降算法
"""
dataMatrix = np.mat(dataMatIn) #转换成numpy矩阵
labelMat = np.mat(classLabels).transpose() # 转置,方便矩阵相乘
m,n = np.shape(dataMatrix) # 获得矩阵维数
alpha = 0.001 # 步长
maxCycles = 500 # 最大迭代次数
weights = np.ones((n,1)) # 初始化回归系数(权重)为1
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights) # 特征值*回归系数
# 计算误差 预测结果-真实值
error = (h-labelMat))
# 根据上面的迭代公式
weights = weights - alpha * dataMatrix.transpose()* error
return weights
# 主程序
dataArr,labelMat = loadDataSet()
weights = gradDecline(dataArr,labelMat)
print(weights)
运行结果如下:
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
上面的代码主要定义了两个函数:
第一个函数是sigmod函数,很简单,直接按照函数来,需要注意的是输入可以是一个向量。
第二函数是梯度下降算法的实现。
这里主要是理解numpy矩阵运算,dataMatrix是100x3矩阵,weights是3x1矩阵,相乘并sigmod得到的h是100x1矩阵;labelMat也是100x1矩阵(已经转置了),所以error也是100x1矩阵;dataMatrix的转置乘以error得到3x1的矩阵,进而weights为3x1的矩阵,实现迭代更新。
根据运行结果可知,500次迭代后,得到了一组回归系数。
3.最佳拟合曲线
得到了最佳拟合参数(回归参数)后,如何更加直观的体现出来呢?这就需要我们通过matplotlib画出决策边界线(最佳拟合曲线)。具体代码如下:
'''
Created on Oct 27, 2010
Logistic Regression Working Module
@author: Peter
@modified by Robert Nie on July 15,2020
'''
import numpy as np
def plotBestFit(weights):
"""
画出最佳拟合曲线
"""
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
# 将dataMat转换成数组形式
dataArr = np.array(dataMat)
# 取行数
n = np.shape(dataArr)[0]
# 定义两类数据坐标
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
# 划分数据
for i in range(n):
if int(labelMat[i])== 1:
#数组索引, 按类别标签,将X1,X2的值分别传给x和y
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
# 画图
fig = plt.figure()
ax = fig.add_subplot(111)
# c表示颜色,maker='s'表示正方形,默认圆形
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
# 坐标尺寸
x = np.arange(-3.0, 3.0, 0.1)
# X2与X1的关系式
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()
dataArr,labelMat = loadDataSet()
weights = gradDecline(dataArr,labelMat)
plotBestFit(weights.getA())
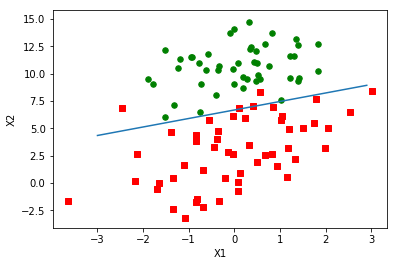
上面这个程序没啥好说的,都是matplot画散点图的格式化步骤,其中getA是array的子函数,功能是将matrix类型转化为array类型。另外,需要注意的地方就是画最佳拟合曲线时,如何确定X2和X1的关系式?
根据sigmod函数,当x=0时,是两类(0类和1类)的分隔点,所以设定:
0 = w 0 x 0 + w 1 x 1 + w 2 x 2 0=w_0x_0+w_1x_1+w_2x_2 0=w0x0+w1x1+w2x2
由于w0=1,所以可以反解出X2和X1的关系式。
根据图像可知,排除个别干扰数据,该拟合曲线的精确度还是蛮高的。
五、总结
这篇文章对logistic回归分类器进行了简要介绍,主要内容包括以下几点:
- Logistic回归的基本概念和应用。
- Sigmod函数的基本概念和性质。
- 梯度下降算法原理。
- python编程,包括数据处理、算法实现和散点图绘制。
参考资料:
- 《机器学习实战》, [美] ,Peter Harriington,人民邮电出版社.
- MOOC-深度学习基础-哈尔滨工业大学-刘远超.
- 百度百科.
- https://cuijiahua.com/blog/2017/11/ml_6_logistic_1.html
基于Python3的Logistic回归源代码下载地址
提取码:z3xu