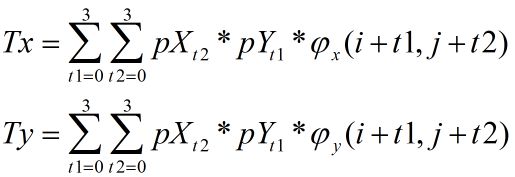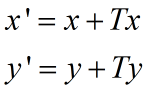图像配准系列之基于B样条的FFD自由变换原理与C++实现
基于B样条的FFD变换属于一种网格型的非刚性形变模型,它按照一定的间距在图像上分布一系列的网格点,使用网格点的位置来计算每个像素点的坐标偏移,最后根据坐标偏移对图像进行像素重采样,实现其非刚性形变。
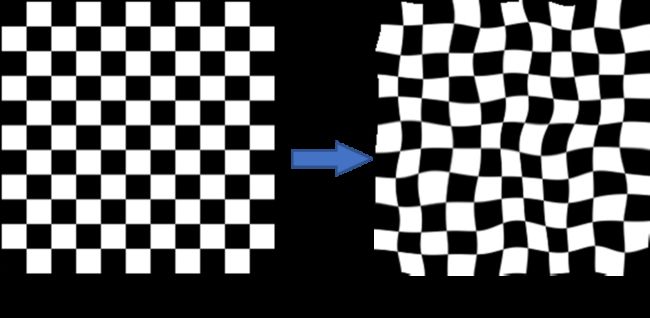
在图像配准中,通常需要根据图像的形变特性选择一种合适的形变模型,如果图像整体运动比较大,则选择整体平移、仿射变换等整体变换模型,如果图像局部形变比较大,则选择薄板样条变换、FFD变换等具有局部特性的变换模型。如下图所示,FFD变换模型具有局部扭曲的特性:
1. FFD计算原理
假设有一张m行n列的图像,如下图中的紫色区域,使用一张r+3行c+3列的网格来覆盖在这张图像上面,其中网格节点称为控制点,每个控制点对应2个控制参数φx和φy,分别为x方向和y方向的控制参数,因此总共有(r+3)*(c+3)*2个控制参数。FFD变换的核心思想是使用每个像素点周围4*4个控制点的控制参数来计算它的位置偏移。之所以网格的行与列都加3,是为了确保图像的边缘点(如下图中的红点)也可以取到其周围4*4的网格节点。
对于m*n的FFD形变图像的任意像素点(x, y),现在我们来计算它相对于原图像的坐标变偏移量。
(1) 计算该像素点的浮点型网格坐标(x_block, y_block)、整型网格坐标(j, i),以及浮点型网格坐标的小数部分(u, v)。
如下式所示,其中的floor表示对浮点数向下取整,也即把其小数部分截断掉,只取整数部分,比如floor(1.25)的结果为1。
(2) 计算形变的权重系数。
权重系数分为x方向与y方向,各4个系数:pX0~pX3与pY0~pY3。
上式中的BsplineBase函数为B样条的基函数:
(3) 计算坐标偏移并插值。
假设点(x, y)的坐标偏移量为(Tx, Ty),那么(Tx, Ty)按以下公式计算:
得到坐标偏移量之后,就得到形变之后的对应坐标(x', y'):
(x, y)为形变图像的坐标,(x', y')为对应的原图像上的坐标。由于(x', y')为浮点坐标,因此需要插值计算其像素值,然后再把插值计算得到的像素值赋值给形变图像的点(x, y)。考虑到最邻近插值容易出现边缘锯齿,因此我们使用双线性插值:
上式中,I为原图像,I'为形变图像。
2. 代码实现
核心代码如下:
void Bspline_Ffd(Mat srcimg, Mat &dstimg, int row_block_num, int col_block_num, Mat grid_points)
{
dstimg.create(srcimg.size(), srcimg.type());
float delta_x = srcimg.cols*1.0/col_block_num;
float delta_y = srcimg.rows*1.0/row_block_num;
int grid_rows = row_block_num + BPLINE_BOARD_SIZE;
int grid_cols = col_block_num + BPLINE_BOARD_SIZE;
int grid_size = grid_rows*grid_cols;
float pX[4], pY[4];
for (int y = 0; y < srcimg.rows; y++) //B_spline 变形
{
for (int x = 0; x < srcimg.cols; x++)
{
float y_block = y / delta_y;
float x_block = x / delta_x;
int i = floor(y_block);
int j = floor(x_block);
float u = x_block - j;
float v = y_block - i;
//使用基函数计算权重系数
pX[0] = (1 - u*u*u + 3*u*u - 3*u) / 6.0;
pX[1] = (4 + 3*u*u*u - 6*u*u) / 6.0;
pX[2] = (1 - 3*u*u*u + 3*u*u + 3*u) / 6.0;
pX[3] = u*u*u / 6.0;
pY[0] = (1 - v*v*v + 3*v*v - 3*v) / 6.0;
pY[1] = (4 + 3*v*v*v - 6*v*v) / 6.0;
pY[2] = (1 - 3*v*v*v + 3*v*v + 3*v) / 6.0;
pY[3] = v*v*v / 6.0;
float Tx = 0;
float Ty = 0;
for (int m = 0; m < 4; m++)
{
for (int n = 0; n < 4; n++)
{
int control_point_x = j + n;
int control_point_y = i + m;
float temp = pY[m] * pX[n];
Tx += temp*grid_points.at(0, control_point_y*grid_cols+control_point_x); //x
Ty += temp*grid_points.at(0, control_point_y*grid_cols+control_point_x+grid_size); //y
}
}
float src_x = x + Tx;
float src_y = y + Ty;
int x1 = cvFloor(src_x);
int y1 = cvFloor(src_y);
if (x1 < 1 || x1 >= srcimg.cols-1 || y1 < 1 || y1 >= srcimg.rows-1)//越界
{
dstimg.at(y, x) = 0;
}
else
{
//dstimg.at(y, x) = srcimg.at(y1, x1); //最邻近插值
int x2 = x1 + 1;
int y2 = y1 + 1;
uchar pointa = srcimg.at(y1, x1);
uchar pointb = srcimg.at(y1, x2);
uchar pointc = srcimg.at(y2, x1);
uchar pointd = srcimg.at(y2, x2);
uchar gray = (uchar)((x2 - src_x)*(y2 - src_y)*pointa - (x1 - src_x)*(y2 - src_y)*pointb - (x2 - src_x)*(y1 - src_y)*pointc + (x1 - src_x)*(y1 - src_y)*pointd);
dstimg.at(y, x) = gray;
}
}
}
}
以上代码中,row_block_num为网格中每行的控制点数,col_block_num为网格中每列的控制点数,grid_points为控制参数,它是一个2行(row_block_num+3)*(col_block_num+3)列的矩阵,第一行是x方向的控制参数,第2行是y方向的控制参数。为了测试以上实现的FFD形变,我们再来写一个初始化控制参数的函数,其功能是随机生成2*(row_block_num+3)*(col_block_num+3)个范围在min~max之间的随机数作为控制参数:
#define randf(a, b) (((rand()%10000+rand()%10000*10000)/100000000.0)*((b)-(a))+(a))
void init_bpline_para(Mat src, int row_block_num, int col_block_num, Mat &grid_points, float min, float max)
{
int grid_rows = row_block_num + BPLINE_BOARD_SIZE;
int grid_cols = col_block_num + BPLINE_BOARD_SIZE;
int grid_size = grid_rows*grid_cols;
grid_points.create(Size(2*grid_size, 1), CV_32FC1);
float *grid_points_data = grid_points.ptr(0);
srand((unsigned int)time(NULL));
for (int i = 0; i < grid_size; i++)
{
grid_points_data[i] = randf(min, max); //x
int cnt = 100000000;
while(cnt--);
grid_points_data[i+grid_size] = randf(min, max); //y
cnt = 100000000;
while(cnt--);
}
}
测试代码如下:
void ffd_test(void)
{
Mat img = imread("lena.jpg", CV_LOAD_IMAGE_GRAYSCALE);
int row_block_num = 30;
int col_block_num = 30;
Mat grid_points;
init_bpline_para(img, row_block_num, col_block_num, grid_points, -10, 10);
Mat out;
Bspline_Ffd(img, out, row_block_num, col_block_num, grid_points);
imshow("img", img);
imshow("out", out);
waitKey();
}
运行以上代码,对496*472的Lena图像进行FFD形变,得到结果如下。可以看到,图像被扭曲了,这是因为我们把控制参数在一定范围内随机化了。
原图像
FFD形变图像
以上实现的代码对496*472的Lena图像进行FFD形变,耗时约52毫秒,在图像配准中需要频繁计算FFD形变,因此总体会非常耗时,故我们使用CUDA来并行优化以上代码:
__global__ void Bspline_Ffd_kernel(uchar *srcimg, uchar *dstimg, int row_block_num, int col_block_num, float *grid_points, int row, int col)
{
int x = threadIdx.x + blockDim.x * blockIdx.x; //col
int y = threadIdx.y + blockDim.y * blockIdx.y; //row
if(x < col && y < row)
{
int grid_rows = row_block_num + BPLINE_BOARD_SIZE;
int grid_cols = col_block_num + BPLINE_BOARD_SIZE;
int grid_size = grid_rows*grid_cols;
float delta_x = col*1.0/col_block_num;
float delta_y = row*1.0/row_block_num;
float x_block = x / delta_x;
float y_block = y / delta_y;
int j = floor(x_block);
int i = floor(y_block);
float u = x_block - j;
float v = y_block - i;
float pX[4], pY[4];
pX[0] = (1 - u*u*u + 3*u*u - 3*u) / 6.0;
pX[1] = (4 + 3*u*u*u - 6*u*u) / 6.0;
pX[2] = (1 - 3*u*u*u + 3*u*u + 3*u) / 6.0;
pX[3] = u*u*u / 6.0;
pY[0] = (1 - v*v*v + 3*v*v - 3*v) / 6.0;
pY[1] = (4 + 3*v*v*v - 6*v*v) / 6.0;
pY[2] = (1 - 3*v*v*v + 3*v*v + 3*v) / 6.0;
pY[3] = v*v*v / 6.0;
float Tx = 0;
float Ty = 0;
for (int m = 0; m < 4; m++) //行
{
for (int n = 0; n < 4; n++) //列
{
int control_point_x = j + n;
int control_point_y = i + m;
float temp = pY[m] * pX[n];
Tx += temp*grid_points[control_point_y*grid_cols+control_point_x]; //x
Ty += temp*grid_points[control_point_y*grid_cols+control_point_x+grid_size]; //y
}
}
float src_x = x + Tx;
float src_y = y + Ty;
int x1 = floor(src_x);
int y1 = floor(src_y);
if (x1 < 1 || x1 >= col-1 || y1 < 1 || y1 >= row-1)//越界
{
dstimg[y*col+x] = 0;
}
else
{
//dstimg[y*col+x] = srcimg[y1*col+x1]; //最邻近插值
int x2 = x1 + 1; //双线性插值
int y2 = y1 + 1;
uchar pointa = srcimg[y1*col+x1];
uchar pointb = srcimg[y1*col+x2];
uchar pointc = srcimg[y2*col+x1];
uchar pointd = srcimg[y2*col+x2];
uchar gray = (uchar)((x2 - src_x)*(y2 - src_y)*pointa - (x1 - src_x)*(y2 - src_y)*pointb - (x2 - src_x)*(y1 - src_y)*pointc + (x1 - src_x)*(y1 - src_y)*pointd);
dstimg[y*col+x] = gray;
}
}
}
void Bspline_Ffd_cuda(Mat srcimg, Mat &dstimg, int row_block_num, int col_block_num, Mat grid_points)
{
dim3 Bpline_Block(16, 16); //每个线程块有16*16个线程
int M = (srcimg.cols+Bpline_Block.x-1)/Bpline_Block.x;
int N = (srcimg.rows+Bpline_Block.y-1)/Bpline_Block.y;
dim3 Bpline_Grid(M, N);
int grid_rows = row_block_num + BPLINE_BOARD_SIZE;
int grid_cols = col_block_num + BPLINE_BOARD_SIZE;
int grid_size = grid_rows*grid_cols;
int img_size = srcimg.cols*srcimg.rows;
uchar *srcimg_cuda;
uchar *dstimg_cuda;
float *grid_points_cuda;
cudaMalloc((void**)&srcimg_cuda, img_size);
cudaMalloc((void**)&dstimg_cuda, img_size);
cudaMalloc((void**)&grid_points_cuda, 2*grid_size*sizeof(float));
cudaMemcpy(srcimg_cuda, srcimg.data, img_size, cudaMemcpyHostToDevice);
cudaMemcpy(grid_points_cuda, grid_points.data, 2*grid_size*sizeof(float), cudaMemcpyHostToDevice);
Bspline_Ffd_kernel<< > >(srcimg_cuda, dstimg_cuda, row_block_num, col_block_num, grid_points_cuda, srcimg.rows, srcimg.cols);
Mat tmp(srcimg.size(), CV_8UC1);
cudaMemcpy(tmp.data, dstimg_cuda, img_size, cudaMemcpyDeviceToHost);
tmp.copyTo(dstimg);
cudaFree(srcimg_cuda);
cudaFree(dstimg_cuda);
cudaFree(grid_points_cuda);
}
cuda加速之后,对同样的Lena图像进行形变,耗时减少到约3.6毫秒,因此加速效果还是相当显著的。
微信公众号如下,欢迎扫码关注,欢迎私信技术交流: