ccf csp 201412-2Z字形扫描（python）

历年题解 CCF CSP历年题解（python）

样例输入：

4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

题目链接：201412-2Z字形扫描

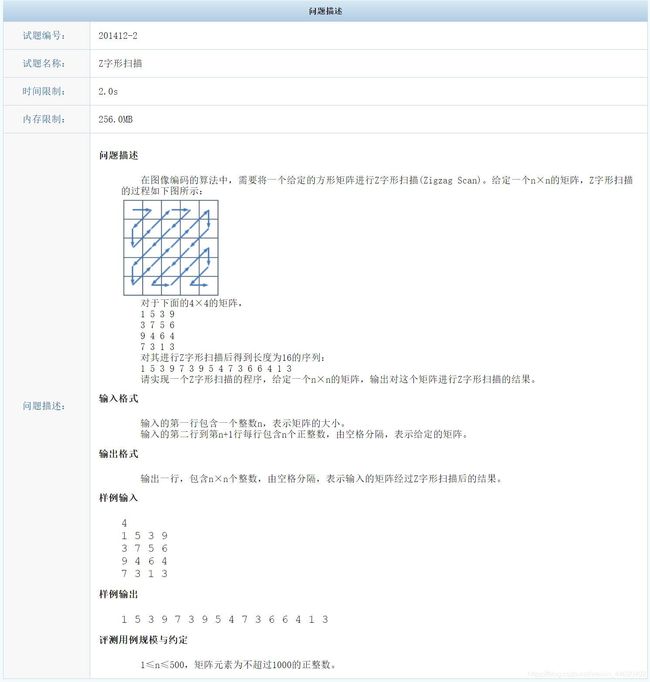
问题分析： 初始点为[0，0]，之后将纵/横向移动与之后紧跟的斜向看作一组，即右移一位，左下方移一位看作一组；再将向下移一位，右上方移两位看作一组，则一共是4+3=7组，最后再加上[n-1,n-1]最后一个点

满分例程：

n=int(input())
s=[]
for i in range(n):
    s+=[list(map(int,input().split()))]
bl=1
l=[s[0][0]]
x=0;y=0#x是行y是列
def Z(x,y,number,bl):#斜向移动函数
    for i in range(number):
        x=x+bl
        y=y-bl
        l.append(s[x][y])
    bl=-bl
    return x,y,bl

for i in range(n-1):#循环结束移动到[0，n-1]
    if bl==1:
        y+=1
    else:
        x+=1
    l.append(s[x][y])
    x,y,bl=Z(x,y,i+1,bl)

for i in range(n-2):#剩下移动
    if bl==-1:
        y+=1
    else:
        x+=1
    l.append(s[x][y])
    x,y,bl=Z(x,y,n-i-2,bl)


l.append(s[n-1][n-1])#加上最后一点
print(l[0],end='')
for i in range(1,n*n):
    print('',l[i],end='')

第二种做法（之前写的）：未构造函数，斜向和纵向分别利用两个坐标增量计算，且里面未用类数组方式存储，而用的列表，索引相对于是坐标的[x*n+y]

n=int(input())
s=[]
for i in range(n):
    s+=list(map(int,input().split()))
l=[s[0]]
a=0
b=1#a,b横向移位
c=1
d=-1#c,d斜向移位
x=0
y=0
count=1#斜向移位计数
for i in range(n-1):
    x+=a
    y+=b
    l+=[s[x*n+y]]
    for j in range(count):
        x+=c
        y+=d
        l+=[s[x*n+y]]
    c,d=d,c
    count+=1
    a,b=b,a
count-=2
for i in range(n-2):
    a,b=b,a
    x+=a
    y+=b
    l+=[s[x*n+y]]
    for j in range(count):
        x+=c
        y+=d
        l+=[s[x * n + y]]
    c,d=d,c
    count -= 1
l+=[s[-1]]
print(l[0],end='')
for i in range(1,n*n):
    print('',l[i],end='')