第十章 keras 人工神经网络

第十章 keras 人工神经网络

10.1.3 感知机

import numpy as np

from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron

iris = load_iris() # type: sklearn.utils.Bunch

iris.target_names

array(['setosa', 'versicolor', 'virginica'], dtype='

iris.target

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

iris.data[:5]

array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2]])

X = iris.data[:, (2, 3)] # petal length, petal width

y = (iris.target == 0).astype(np.int)

per_clf = Perceptron()
per_clf.fit(X, y)

Perceptron()

y_pred = per_clf.predict([[2, 0.5]])
print(y_pred)

[0]

10.1.4 MLP

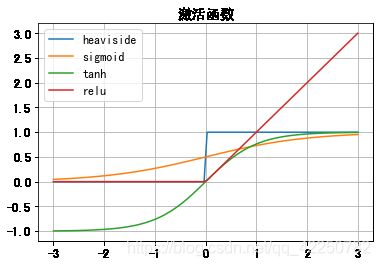
激活函数

• 越阶函数
• sigmoid函数
  -双曲正切函数
  -线性整流单位函数

from matplotlib import pyplot as plt
%matplotlib inline

font = {
     'family' : 'SimHei',
    'weight' : 'bold',
     'size'   : '12'}
plt.rc('font', **font)          # 步骤一（设置字体的更多属性）
plt.rc('axes', unicode_minus=False)  # 步骤二（解决坐标轴负数的负号显示问题）

line_x = np.linspace(-3, 3, 100)
def heaviside(x):
    # 越阶函数
    return 0 if x <= 0 else 1

def sigmoid(x):
    # sigmoid 逻辑回归函数
    return 1 / ( 1 + np.exp(-x))

def tanh(x):
    # 双曲正切函数
    y = ( np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
    return y
    # 或者
    #return 2 * sigmoid(2 * x) - 1
    
def relu(x):
    # 线性整流单位函数
    return max(0, x)

y_heaviside = np.vectorize(heaviside, otypes=[np.float64])(line_x)
y_sigmoid = np.vectorize(sigmoid, otypes=[np.float64])(line_x)
y_tanh = np.vectorize(tanh, otypes=[np.float64])(line_x)
y_relu = np.vectorize(relu, otypes=[np.float64])(line_x)

plt.grid(True)
plt.plot(line_x, y_heaviside, 
         line_x, y_sigmoid, 
         line_x, y_tanh, 
         line_x, y_relu
        )
plt.legend(('heaviside', 'sigmoid', 'tanh', 'relu'), loc="upper left")
plt.title("激活函数")

Text(0.5, 1.0, '激活函数')

10.2 使用Keras实现MLP

import tensorflow as tf
from tensorflow import keras
tf.__version__

'2.4.1'

keras.__version__

'2.4.0'

10.2.2 使用顺序API构建图像分类器

fashion_mnist = keras.datasets.fashion_mnist

(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz
8192/5148 [===============================================] - 0s 2us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz
4423680/4422102 [==============================] - 3s 1us/step

type(X_train_full)

numpy.ndarray

X_train_full.shape, X_train_full.dtype

((60000, 28, 28), dtype('uint8'))

X_valid, X_train = X_train_full[: 5000] / 255.0, X_train_full[5000: ] / 255.0
y_valid, y_train = y_train_full[:5000], y_train_full[5000: ]

class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
              "Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
class_names[y_train[0]]

'Coat'

class_index = np.unique(y_train_full)
print(class_index, type(class_index))

[0 1 2 3 4 5 6 7 8 9] 

picture_one = X_train_full[5000]

import random
from PIL import Image
def get_class_picture_map(X, y):
    #y_length = len(y)
    classes = np.unique(y)
    m = {
     }
    for i in classes:
        # 取出第五个值
        index = np.argwhere(y == i)[5][0]
        m[i] = X[int(index)]
    return m
print(y_train_full.shape)
cls_pic_map = get_class_picture_map(X_train_full, y_train_full)
print(len(cls_pic_map))

(60000,)
10

for i, p in cls_pic_map.items():
#     print(p.shape)
    image_ = Image.fromarray(p).convert("RGB")
    plt.figure(dpi=20)
    plt.imshow(image_)
    plt.axis("off")
    plt.title(class_names[i],fontsize=50)
plt.show()

model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))

# summary显示模型所有层
model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
flatten_1 (Flatten)          (None, 784)               0         
_________________________________________________________________
dense (Dense)                (None, 300)               235500    
_________________________________________________________________
dense_1 (Dense)              (None, 100)               30100     
_________________________________________________________________
dense_2 (Dense)              (None, 10)                1010      
=================================================================
Total params: 266,610
Trainable params: 266,610
Non-trainable params: 0
_________________________________________________________________

# 编译模型
model.compile(loss="sparse_categorical_crossentropy",
             optimizer="sgd", metrics=["accuracy"])

# 训练模型
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))

Epoch 1/20
1719/1719 [==============================] - 8s 4ms/step - loss: 0.9757 - accuracy: 0.6948 - val_loss: 0.5338 - val_accuracy: 0.8212
Epoch 2/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.5009 - accuracy: 0.8266 - val_loss: 0.4571 - val_accuracy: 0.8446
Epoch 3/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.4512 - accuracy: 0.8410 - val_loss: 0.4102 - val_accuracy: 0.8562
Epoch 4/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.4188 - accuracy: 0.8516 - val_loss: 0.4319 - val_accuracy: 0.8498
Epoch 5/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.4018 - accuracy: 0.8590 - val_loss: 0.3761 - val_accuracy: 0.8688
Epoch 6/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3874 - accuracy: 0.8623 - val_loss: 0.3916 - val_accuracy: 0.8634
Epoch 7/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3681 - accuracy: 0.8718 - val_loss: 0.3972 - val_accuracy: 0.8620
Epoch 8/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3598 - accuracy: 0.8715 - val_loss: 0.3550 - val_accuracy: 0.8746
Epoch 9/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3433 - accuracy: 0.8750 - val_loss: 0.3514 - val_accuracy: 0.8728
Epoch 10/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3349 - accuracy: 0.8799 - val_loss: 0.3512 - val_accuracy: 0.8754
Epoch 11/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3185 - accuracy: 0.8861 - val_loss: 0.3562 - val_accuracy: 0.8702
Epoch 12/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3198 - accuracy: 0.8852 - val_loss: 0.3404 - val_accuracy: 0.8776
Epoch 13/20
1719/1719 [==============================] - 8s 5ms/step - loss: 0.3108 - accuracy: 0.8885 - val_loss: 0.3316 - val_accuracy: 0.8784
Epoch 14/20
1719/1719 [==============================] - 8s 4ms/step - loss: 0.3085 - accuracy: 0.8882 - val_loss: 0.3419 - val_accuracy: 0.8762
Epoch 15/20
1719/1719 [==============================] - 8s 5ms/step - loss: 0.3017 - accuracy: 0.8916 - val_loss: 0.3321 - val_accuracy: 0.8812
Epoch 16/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.2899 - accuracy: 0.8958 - val_loss: 0.3393 - val_accuracy: 0.8768
Epoch 17/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.2842 - accuracy: 0.8978 - val_loss: 0.3240 - val_accuracy: 0.8850
Epoch 18/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.2836 - accuracy: 0.8974 - val_loss: 0.3104 - val_accuracy: 0.8892
Epoch 19/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.2713 - accuracy: 0.9015 - val_loss: 0.3028 - val_accuracy: 0.8914
Epoch 20/20
1719/1719 [==============================] - 7s 4ms/step - loss: 0.2632 - accuracy: 0.9065 - val_loss: 0.3059 - val_accuracy: 0.8918

# 使用fit()函数返回的history, 绘制学习曲线
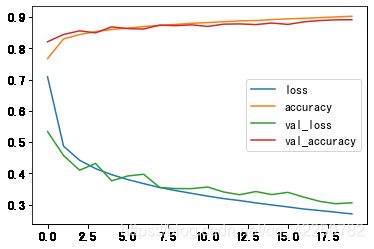
history_df = pd.DataFrame.from_dict(history.history)

history_df.plot()

# 使用模型预测
X_new = X_test[:3]
y_proba = model.predict(X_new)
y_proba.round(3)

array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
       [0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)

# 返回概率高的类
#y_pred = model.predict_classes(X_new) 过时的方法
y_pred = np.argmax(model.predict(X_new), axis=-1)
y_pred

array([9, 2, 1])

np.array(class_names)[y_pred]

array(['Ankle boot', 'Pullover', 'Trouser'], dtype='

for p, i in zip(X_new, y_pred):
#     print(p.shape)
    image_ = Image.fromarray(p).convert("RGB")
    plt.figure(dpi=20)
    plt.imshow(image_)
    plt.axis("off")
    plt.title(class_names[int(i)],fontsize=50)
plt.show()

10.2.3 使用顺序API构建回归MLP

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

housing = fetch_california_housing()

print(type(housing))
# 将数据集分为，训练集与测试集
X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target)

X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full)

# 将数据平移、归一化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
X_test = scaler.transform(X_test)

print(type(X_train), type(X_valid), type(X_test))
print(X_train.shape)

  
(11610, 8)

# 构建模型
from tensorflow import keras
model = keras.models.Sequential([
    keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),
    keras.layers.Dense(1)
])
# 编译模型
model.compile(loss="mean_squared_error", optimizer="sgd")
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))

Epoch 1/20
363/363 [==============================] - 3s 4ms/step - loss: 1.5201 - val_loss: 25.5889
Epoch 2/20
363/363 [==============================] - 1s 2ms/step - loss: 3.2021 - val_loss: 0.4432
Epoch 3/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4294 - val_loss: 0.4002
Epoch 4/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3965 - val_loss: 0.3866
Epoch 5/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3773 - val_loss: 0.3894
Epoch 6/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3703 - val_loss: 0.3856
Epoch 7/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3698 - val_loss: 0.3835
Epoch 8/20
363/363 [==============================] - 1s 2ms/step - loss: 0.7318 - val_loss: 0.3811
Epoch 9/20
363/363 [==============================] - 1s 2ms/step - loss: 0.3576 - val_loss: 0.3776
Epoch 10/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3729 - val_loss: 0.3738
Epoch 11/20
363/363 [==============================] - 1s 2ms/step - loss: 0.3485 - val_loss: 0.3728
Epoch 12/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3535 - val_loss: 0.3759
Epoch 13/20
363/363 [==============================] - 1s 2ms/step - loss: 0.3613 - val_loss: 0.3684
Epoch 14/20
363/363 [==============================] - 1s 2ms/step - loss: 0.3419 - val_loss: 0.3730
Epoch 15/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3581 - val_loss: 0.3701
Epoch 16/20
363/363 [==============================] - 1s 2ms/step - loss: 0.3478 - val_loss: 0.3672
Epoch 17/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3490 - val_loss: 0.3703
Epoch 18/20
363/363 [==============================] - 1s 2ms/step - loss: 0.3351 - val_loss: 0.3683
Epoch 19/20
363/363 [==============================] - 1s 1ms/step - loss: 0.3319 - val_loss: 0.3627
Epoch 20/20
363/363 [==============================] - 1s 2ms/step - loss: 0.3495 - val_loss: 0.3753

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

font = {
     'family' : 'SimHei',
    'weight' : 'bold',
     'size'   : '12'}
plt.rc('font', **font)          # 步骤一（设置字体的更多属性）
plt.rc('axes', unicode_minus=False)  # 步骤二（解决坐标轴负数的负号显示问题）
# 绘制学习曲线
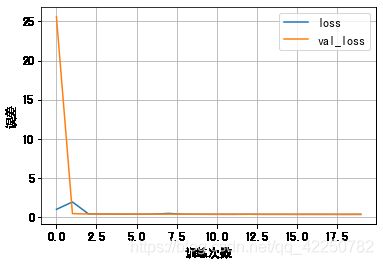
history_df = pd.DataFrame.from_dict(history.history)
history_df.plot()
plt.grid(True)
plt.xlabel("训练次数")
plt.ylabel("误差")
plt.show()

# 验证集评估泛化性能
mse_test = model.evaluate(X_test, y_test)

162/162 [==============================] - 0s 1ms/step - loss: 0.3848

# 使用model预测数据
X_new = X_test[:3]
y_pred = model.predict(X_new)

print(y_pred)
print(y_test[:3])

[[2.189899 ]
 [1.6507447]
 [1.7364986]]
[1.875 1.647 2.239]