论文翻译-Defense against Universal Adversarial Perturbations
CVPR2018-防御通用对抗扰动
论文下载地址:https://arxiv.org/abs/1711.05929
论文源代码:https://github.com/liujianee/Pertrubation_Rectifying_Network
摘要
深度学习中的最近研究表明存在图像无关的微小扰动,能够被应用于任何图像来愚弄先进的网络分类器,从而改变图像标签的预测结果。这些通用对抗扰动对深度学习在实际中的使用产生了严重的威胁。我们提出了第一个专用的框架来帮助网络防御这些扰动。我们的方法学习了一个扰动修正网络(PRN)作为目标模型的预输入层,这样就不需要修改目标模型。PRN通过真实和合成的图像无关的扰动学习生成,同时还提出了一种计算合成扰动的方法。一个扰动检测器单独训练在PRN的输入-输出差的离散余弦变换上。一张查询图像首先通过PRN,同时使用检测器检验。如何扰动被检测到,PRN的输出就会作为模型输入进行预测,而不是原始图像。一个严谨的评价显示,我们的框架能够帮助网络分类器在真实世界场景防御不可见的对抗扰动,达到97.5%的成功率。PRN能够在一个目标模型上训练之后,帮助其他模型进行防御,并且有一个较好的成功率。
1.引言
神经网络是目前计算机视觉和模式识别这些先进领域的核心,在许多具有挑战性的任务上[9][12][14][16][36][37]实现了很好的效果。虽然如此,Moosavi-Dezfooli[25]等人展示了使用通用对抗扰动直接对任意图像直接进行扰动来愚弄深度网络,从而改变预测的可能性。对于一个给定的网络模型,这些图像无关(所以通用)的扰动能够比较容易的计算[25][26]。这些扰动保持不可见(Figure 1),通过将扰动添加到图像上生成对抗样本,仍然可以以高得惊人的概率愚弄网络[25]。另外,愚弄能够在不同的网络模型之间很好的推广。
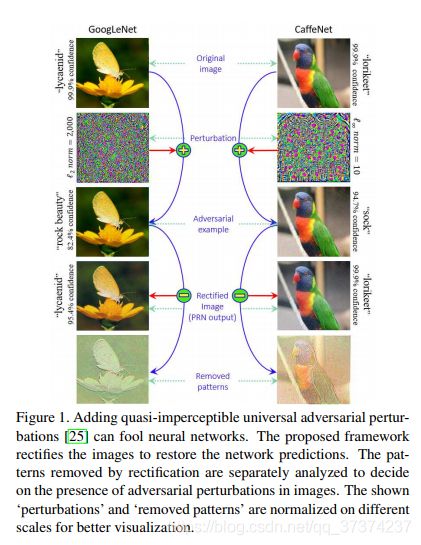
因为是图像无关的,通用对抗扰动能够很方便的用来愚弄模型,在没有使用过的图像上通过预计算的扰动进行攻击。这杜绝了在生成特定图像扰动时的无限制的计算能力的需求[7][21]。通用扰动的跨模型泛化能力,使得它们与实际环境特别相关,一个模型可能被部署在一个敌对的环境中。因此,防御这些扰动对于深度学习在实践中的成功时必须的。考虑到被对抗扰动修改的真实场景(比如路上的信号灯)会对网络表现为对抗样本,对这些扰动的防范措施很明显是需要的[17]。
这个工作提出了第一个针对通用对抗扰动的防御方法[25]。这篇论文主要的贡献如下:
- 我们提出训练一个扰动修正网络(PRN)作为目标模型的预输入。这使得我们的框架可以在不修改模型的情况下对已经部署的网络提供防御。
- 我们提出了一种高效的计算合成的图像无关的对抗扰动的方法,可以高效的训练PRN。这些扰动的成功生成实现了Moosaci-dezfooli[26]的了理论发现。
- 我们提出了一个单独的扰动检测器。它通过PRN对于干净和扰动样本的图像校正的离散余弦变换来进行训练。
- 通过对GoogLeNet[37]CaffeNet[16]VGG-F network[4]进行防御进行严格的评测,结果显示,对于可能被不可见的扰动修改的没有使用过的图像,达到了97.5的成功率。我们的实验也证明了提出的PRN能够在不同的网络模型之间推广。
2.相关工作
在最近几年,图像分类器针对对抗样本的鲁棒性获得了广泛的关注[6][7][29][32][34][35][40]。在Szegedy[39]等人第一次展示了对于这些网络而言对抗扰动的存在以后,深度神经网络成为了这些领域关注的核心。学习[1]中对于这个方向最近文献的评价。Szegedy[39]等人通过对图像添加不可知的扰动来计算网络的对抗样本,这些扰动是通过最大化网络的预测错误来估计的。尽管这些扰动是图像相关的,但是这些同样的扰动图像可以愚弄多个网络模型。Szegedy等人提出了通过使用对抗样本进行训练也叫做对抗训练的方法来提高模型对于对抗攻击的鲁棒性。
Goodfellow[10]等人基于[39]的发现,提出了一种快速梯度信号方法来有效的生成对抗样本,能够用来训练网络。他们假设正是深度网络的线性特性使它们容易受到对抗性扰动的影响。虽然如此,Tanay和Griffin[41]为线性分类器构造不受对抗样本影响的图像类。他们关于对抗扰动存在的争论再次指向了正则化可以缓解的过拟合现象。然而现在仍然不清楚一个网络应该如何正则化来提高针对对抗样本的鲁棒性。
Moosavi-Dezfooli[27]提出了DeepFool算法,通过假设网络对于目前训练的样本的损失函数是线性化的来计算图像依赖的对抗扰动。和单步扰动估计[10]相反的是,他们的方法以迭代的方式计算扰动。他们同样展示了通过对抗样本增加训练数据显著的增加了网络对于对抗样本的鲁棒性。Baluja和Fischer[2]训练一个对抗转移网络来对目标模型生成对抗样本。Lin[19]等人评价了对抗样本的转移性。他们研究了有目标和无目标样本的这个性质,提出了基于全体的有更好转移性的生成样本的方法。
上述的技术主要集中在生成对抗样本,通过对抗训练解决对这些样本的防御问题。与我们对这个问题的看法一致,最近的技术很少有直接集中注意力在防御对抗样本上。比如Lu[22]等人通过使用中心凹来缓和对抗扰动的问题。他们的主要论点是,神经网络(用于ImageNet[33])对由中心凹引起的图像的大小和平移变化具有很强的鲁棒性,但是,这一特性不适用于扰动变换。
Papernot[30]等人使用蒸馏使得神经网络对对抗样本更有鲁棒性。虽然如此,Carlini和Wagner[3]之后介绍的对抗攻击不能使用蒸馏方法防御。Kurakin[18]等人研究了使更大的模型(Inception_V3[38])对扰动鲁棒的对抗训练,发现这种训练对于单步法[10]生成的扰动具有鲁棒性。虽然如此,Tramer[42]等人发现这种鲁棒性对于使用其他网络生成的对抗样本无效,比如黑盒攻击[19]。因此全体对抗训练在[42]中被提出,他使用多个网络生成的对抗样本来训练。
Dziugaite[5]等人研究了JPG压缩对对抗样本的影响,发现压缩有时能够恢复网络的愚弄率。虽然如此,他认为单独的JPG压缩作为防御方法是不充分的。Prakas[31]等人在他们的防御中利用了扰动像素的位置。Lu[20]等人提出了SafetyNet来为卷积神经网络(比如VGG19[11])提供检测,并且拒绝对抗样本,它是利用网络的Relus阶段来检测扰动样本。类似的,一种为神经网络添加检测子网络的想法被Metzen[23]等人提出。除了分类器,对抗样本和神经网络防御的鲁棒性最近也在语义分割和对象检测等任务中被研究。
然而,上述文献的关键主题都是计算单个图像的扰动,Moosavi-Dezfooli[25]是第一个展示了网络的图像无关的扰动。这些扰动在[26]中被评价,然而Metzen[24]等人也展示了图像语义分割领域的存在。目前为止,没有专门的为网络防御通用对抗扰动的技术,这也是这篇文论文的核心。
3.问题定义
接下来,我们展示了通用对抗扰动和防御扰动更正式的概念。让 S c ~ ∈ R d \widetilde{S_{c}}\in R^{d} Sc ∈Rd定义为干净数据在d维空间的分布,这样一个类别标签就和,每个样本 I c ∼ S c ~ I_{c}\sim \widetilde{S_{c}} Ic∼Sc 联系在一起。让 C C C作为一个分类器(一个深度网络),把图像映射到它的类别标签: C ( I c ) : I c → l ∈ R C(I_{c}):I_{c}\rightarrow l\in R C(Ic):Ic→l∈R。向量 ρ ∈ R d \rho \in R^{d} ρ∈Rd是分类器的通用对抗扰动,他满足下面的限制:
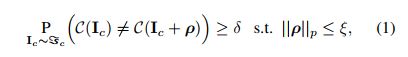
其中 P P P是可能性, ∣ ∣ . ∣ ∣ p ||.||_{p} ∣∣.∣∣p定义了向量的 l p l_{p} lp范式,其中 p ∈ [ 1 , ∞ ) p\in [1,\infty) p∈[1,∞), δ ∈ ( 0 , 1 ] \delta\in (0,1] δ∈(0,1]定义了愚弄了, ξ \xi ξ是预定义的常数。在下面一部分,我们把 ρ \rho ρ作为一个简洁的扰动。
在**(1)** 中,问题中的扰动是图像无关的,因此Moosavi-Dezfooli[25]等人定义为通用。根据阐明的定义,参数 ξ \xi ξ限制了扰动的大小。对于不可见的扰动,这个参数的值和图像大小 ∣ ∣ I c ∣ ∣ p ||I_{c}||_{p} ∣∣Ic∣∣p相比一个非常小。另一方面,一个大的 δ \delta δ要求扰动能够以较大的可能性愚弄分类器。在这个工作中,我们设置 δ ≥ 0.8 \delta\geq 0.8 δ≥0.8并且考虑扰动的 l 2 l_{2} l2和 l ∞ l_{\infty} l∞范式限制。对于 l 2 l_{2} l2范式,我们设置 ξ = 2000 \xi=2000 ξ=2000,对于 l ∞ l_{\infty} l∞范式我们设置 ξ = 10 \xi=10 ξ=10。在两种类型中,实验中的值都设置为图像大小平均值的4%左右,和[25]相同。
为了帮助 C C C防御扰动,我们设置两个防御机制的组件。(1)扰动检测器 D ( I ρ / c ) D(I_{\rho/c}) D(Iρ/c): I ρ / c → [ 0 , 1 ] I_{\rho/c}\rightarrow [0,1] Iρ/c→[0,1]。(2)扰动修正器 R ( I ρ ) R(I_{\rho}) R(Iρ): I ρ → I ^ I_{\rho}\rightarrow \widehat{I} Iρ→I ,其中 I ρ = I c + ρ I_{\rho}=I_{c}+\rho Iρ=Ic+ρ。检测器决定了一张未使用的图像是干净的还是对抗的。修正器的目的是计算一个扰动图像的转移 I ^ \widehat{I} I ,使得 P I c ∼ S c ~ ( C ( I ^ ) = C ( I c ) ) ≈ 1 \underset{I_{c}\sim\widetilde{S_{c}}}{P}(C(\widehat{I})=C(I_{c}))\approx 1 Ic∼Sc P(C(I )=C(Ic))≈1。注意,除了分类器在干净数据上的表现外,修正器并不提高修正图像的预测效果。这确保了 R R R稳定的感应。另外,公式允许我们计算 I ^ \widehat{I} I 使得 ∣ ∣ I ^ − I c > 0 ||\widehat{I}-I_{c}>0 ∣∣I −Ic>0。我们利用这个性质去学习 R R R,让它作为端到端的分类器 C C C的预输入层。
4.提出的方法
我们利用第二章回顾的文献,来提出一种框架帮助目标网络模型防御通用对抗扰动。Figure 2展示了我们学习防御框架中修正器和检测器方法的原理图。我们使用扰动修正网络(PRN)作为修正器,同时训练一个二分类模型去检测图像中的对抗扰动。框架使用真实和合成的扰动进行训练。提出的框架结构将在下面解释。
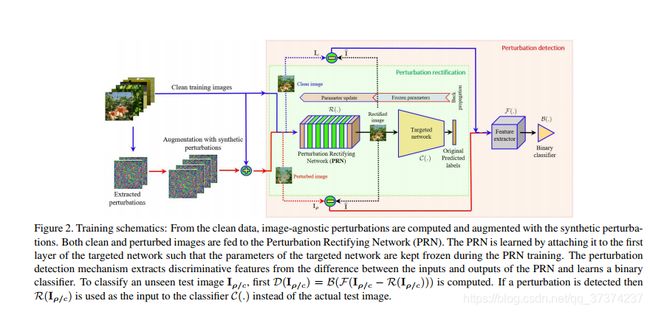
我们技术的核心是扰动修正网络(PRN),它被训练作为目标网络的预输入层。PRN被连接到分类网络的第一层,联合网络通过训练最小化下面的损失:

其中 l ∗ i l i l^{i}_{*} l_{i} l∗ili是联合网络和目标网络的预测标签, l i l_{i} li必须对干净数据进行计算。对于N个训练样本。 L L L计算损失,其中 θ p b p \theta_{p} b_{p} θpbp是PRN的权重和偏置。
在**(2)** 中,我们仅仅定义了PRN参数的损失函数,确保(早已部署)目标网络不需要因为我们的框架提供的防御而做任何修改。这个策略和现有的通过对抗训练更新目标模型提升鲁棒性的方法[18][42]、或者将架构更改合并到目标网络中,其中可能包括将子网添加到模型中的方法[23]、或者利用某些层的激活来检测对抗样本的方法[20]不同。我们的防御机制作为目标网络的外部包装,训练用来来对抗对抗攻击的PRN(和检测器)可以保持隐蔽,以防御潜在的对抗攻击。这是真实世界场景中的防御框架非常需要的性质。Moosavi-Dezfooli[25]提出,通用对抗扰动会一直存在,即使模型经过了对抗训练。提出的框架从本质上满足了这个要求。
我们使用干净和对抗样本来训练PRN,防止我们的网络学习的图像转移偏向于对抗样本。对于训练, l i l_{i} li是目标模型对于 i t h i^{th} ith训练样本的干净版本的单独计算。PRN模型是使用被卷积层夹住大的5-ResNet块[12]实现的。224x224x3的输入图像使用Conv 3x3,stride=1,feature maps=64,'same’的卷积。连接着5-ResNet块,每个块包含两个具有Relu[28]激活的卷积层,生成64个特征映射。最后一个ResNet块的特征映射使用Conv 3x3,stride=1,feature maps=16,'same’卷积;之后是Conv 3x3,stride=1,feature maps=3,'same’卷积。
我们使用交叉熵损失[9]和ADAM优化器来训练PRN。第一个和第二个动量的衰减常数设置为0.9和0.999.我们设置初始学习率为0.01,在每1000次迭代后10%的比例下降。我们使用64的小批量数据,训练目标网络的PRN至少需要5个epoch。
4.2.训练数据
PRN使用干净数据和对应的天剑扰动的对抗版本进行训练。我们在继续计算之前首先根据Moosavi-Dezfooli[25]的方法生成扰动集合 ρ ∈ P ⊆ R d \rho\in P\subseteq R^{d} ρ∈P⊆Rd。他们的算法以一个迭代的方式计算通用对抗扰动。在他们的内部循环中(在训练数据上运行),算法寻找一个最小的向量在一张图像上愚弄模型。目前的 ρ \rho ρ的估计是通过添加寻找的向量,然后映射到半径为 ε \varepsilon ε的 l p l_{p} lp球内。外部的循环确保在完整的数据集上实现了想要的愚弄率。总的来说,算法要求在训练集上几次全部使用确保可接受的愚弄率。我们参考[25]获得算法更多的细节。
在训练中有更多对抗图案的训练好的PR认为有更好的表现。虽然如此,使用上面提到的算法生成大数量(多余100)的扰动需要很大的计算量。因此,我们设计一个机制来高效的生成合成扰动 ρ s ∈ P s ⊆ R d \rho_{s}\in P_{s}\subseteq R_{d} ρs∈Ps⊆Rd,作为PRN的训练集。合成扰动使用利用[26]的理论生成的集合 P P P来进行计算合成。为了生成合成的扰动,我们计算的向量满足下面的关系:(c1) ρ s ∈ Ψ p + \rho_{s}\in \Psi^{+}_{p} ρs∈Ψp+: Ψ p + = P \Psi^{+}_{p}=P Ψp+=P元素子空间的正交。(c2) ∣ ∣ ρ s ∣ ∣ 2 ≈ E [ ∣ ∣ ρ ∣ ∣ 2 , ∀ ρ ∈ P ] ||\rho_{s}||_{2}\approx E[||\rho||_{2},\forall\rho\in P] ∣∣ρs∣∣2≈E[∣∣ρ∣∣2,∀ρ∈P]和(c3) ∣ ∣ ρ s ∣ ∣ ∞ ≈ ξ ||\rho_{s}||_{\infty}\approx \xi ∣∣ρs∣∣∞≈ξ。通过 l ∞ l_{\infty} l∞范式限制的扰动生成方法在Algorithm 1,中进行了总结。我们在论文补充材料部分实现了计算 l 2 l_{2} l2范式的扰动。
为了生成合成扰动,Algorithm 1 在 P P P中元素单元向量控制的方向上使用随机步数在 Ψ P + \Psi^{+}_{P} ΨP+中寻找 ρ s \rho_{s} ρs。随机走动一直继续,直到 ρ s \rho_{s} ρs的 l ∞ l_{\infty} l∞范式始终比 ξ \xi ξ小。算法寻找一个 ρ s \rho_{s} ρs,如果向量的 l 2 l_{2} l2范式和在 P P P中期望的向量相差无几的时候,就作为一个有效的扰动。对于生成 l 2 l_{2} l2范式的扰动,补充材料中给出了相应的算法终止在line-4的基于 ∣ ∣ ρ s ∣ ∣ 2 ||\rho_{s}||_{2} ∣∣ρs∣∣2的随机漫步,直接选择计算的 ρ s \rho_{s} ρs作为所需的扰动。评价深度网络对于对抗样本的鲁棒性,Moosavi-Dezfooli[26]展示了共享方向的存在(跨越不同的数据点),沿着这个方向,由网络引起的决策边界变得高度正向弯曲。这些容易攻击的方向上,存在愚弄网络改变数据点预测标签的微小扰动。我们的算法在这些方向上寻找合成扰动,这些想要的方向来自于 P P P。


Figure 3 展示了我们的算法对于 l 2 l ∞ l_{2} l_{\infty} l2l∞范式生成的典型的合成扰动。它还展示了在集合 P P P中对于给定扰动的对应的最接近的匹配项。合成扰动的愚弄率不如原始扰动高,但是还是在一个可以接受的范围内。在在我们的实验中,使用合成扰动进行训练的讨论有利于早期的收敛和PRN更好的表现。我们注意到,这这次工作中展示的合成扰动愚弄率补充了[26]的理论发现。一旦扰动集合 P s P_{s} Ps计算完成,我们限制 P ∗ = P ⋃ P s P^{*}=P\bigcup P_{s} P∗=P⋃Ps,把它作为寻来你数据的扰动图像。
4.3.扰动检测
尽管研究了JPG压缩作为一种减轻(图像相关)对抗扰动效果的机制,Dziugaite[5]等人建议使用离散余弦变换(DCT)作为一种可能的减轻扰动效果的候选方法。我们展示在补充材料的实验,证明了基于DCT的压缩能够用来减轻网络对于对抗扰动的愚弄率。虽然如此,它很难决定压缩率,尤其是不知道图像到底是不是扰动的。在干净图像上不必要的修正常常会降低网络的表现。
不使用DCT来移除扰动,我们利用它来进行我们方法的扰动检测。使用包含干净和扰动图像的训练集,记为 I ρ / c t r a i n I^{train}_{\rho/c} Iρ/ctrain,我们首先计算 F ( I r h o / c t r a i n − R ( I ρ / c t r a i n ) ) F(I^{train}_{\\rho/c}-R(I^{train}_{\rho/c})) F(Irho/ctrain−R(Iρ/ctrain)),然后学习一个二元分类器 B ( F ) → [ 0 , 1 ] B(F)\rightarrow [0,1] B(F)→[0,1],根据数据标签确定干净还是扰动图像。我们实现 F F F来计算讨论中的灰度图像的2D-DCT相关系数的log的绝对值,其中 B B B是通过SVM学习成的。函数 D = B ( F ) D=B(F) D=B(F)组成了我们防御框架的检测器部件。为了分类图像 I ρ / c I_{\rho/c} Iρ/c,我们首先评价 D ( I ρ / c ) D(I_{\rho/c}) D(Iρ/c),如果扰动被检测到, C ( R ( I ρ / c ) ) C(R(I_{\rho/c})) C(R(Iρ/c))来进行分类而不是 C ( I ρ / c ) C(I_{\rho/c}) C(Iρ/c),其中 C C C代表目标网络分类器。
5.实验
我们通过对CaffeNet[16]VGG-F network[4]GoogLeNet[37]防御通用对抗扰动来评价我们方法的表现。网络的选择基于我们实验原则生成扰动的计算需求变化。同样的框架应用到其他网络。与Moosavi-Dezfooli[25]类似,我们选择ILSVRC2012[16]的50000张验证集来进行实验。
Setup: 从可选的图像之中,我们随机选择10000张来对每个网络生成50张图像无关的扰动,扰动中25张限制 l ∞ l_{\infty} l∞范式为10,其他的25张限制为 l 2 l_{2} l2范式为2000.所有网络的愚弄率限制在0.8。另外,在两个同类型( l 2 l ∞ l_{2} l_{\infty} l2l∞)扰动之间,最大的点积上界是0.15。这确保了构造的扰动彼此之间存在显著差异,从而消除了我们评估中的任何潜在偏差。对于25张扰动集合,我们随机选择20张作为训练数据,另外5张作为测试集。
我们通过在4.2章讨论的部分扩展了训练的扰动集合,使得在每个扩展集合中有250张扰动,表示为 P ∞ ∗ P 2 ∗ P^{*}_{\infty} P^{*}_{2} P∞∗P2∗。为了生成训练数据,我们首先从图像中随机选择40000张样本,通过5中裁剪生成224x224x3大小,生成200000张样本。为了创造 l 2 l_{2} l2范式扰动的对抗样本,我们使用集合 P 2 ∗ P^{*}_{2} P2∗,以0.5的可能性随机添加扰动到图像上。这生成了大概100000张干净和扰动图像,对一个给定网络用 l 2 l_{2} l2范式的扰动来训练我们的方法。我们重复这个过程在 P ∞ ∗ P^{*}_{\infty} P∞∗上使用 l ∞ l_{\infty} l∞范式扰动进行训练。注意的是,对于一个目标网络,我们使用两种类型的扰动进行两次训练来评价我们方法的表现。
对一个完全的评测,两种方式都生成了测试数据。两种方式都使用被5种没见过的扰动扰动过的10000张图像。需要注意的是,为了模仿真实世界场景中部署好的网络,评价时一直保持不可见。对于方案A,我们使用全部的10000张测试图像,并且使用5种测试扰动以0.5的概率随机污染图像。对于方案B,我们从10000张测试集中选择最近以干净图像的形式被目标网络分类过的子集合,然后使用5种扰动以0.5的概率随机污染图像。干净数据和扰动数据以等可能的形式存在确保了检测器的公平评价。
Evaluation metric: 我们使用4种不同的来对我们的方法的表现进行综合评价。设置 I c I ρ I_{c} I_{\rho} IcIρ定义为干净和扰动测试图像。类似的,把 I ρ ^ , I ρ / c ^ \widehat{I_{\rho}} ,\widehat{I_{\rho/c}} Iρ ,Iρ/c 定义为包含被PRN修正的测试集的集合,其中 I ρ ^ \widehat{I_{\rho}} Iρ 中的图像都是扰动的(在通过PRN之前), I ρ / c ^ \widehat{I_{\rho/c}} Iρ/c 中以0.5的概率进行类似的扰动,正如我们前面的方案。 I ∗ \overset{*}{I} I∗定义为包含被检测器 D D D分类为扰动的被PRN修正的测试集的集合。另外,把 a c c acc acc定义为目标网络在给定图像集上的计算预测准确率的函数。我们在实验中使用的度量标准的定义如下:

度量标准的名称与与它们相关的语义概念一致。注意的是,请注意,PRN修复是在对干净和扰动的图像进行修正时定义的。我们做这个来解释干净数据被PRN修正后引起的目标模型分类准确率损失。在我们的实验中观察到,对干净数据不必要的修正有时会导致目标网络分类准确率有微小的(1-2%)减少。因此,我们对PRN修复使用一个更严格的定义来获得更易懂得评价。这个定义也符合我们对实际场景的基本假设,在这些场景中,我们不知道测试图像是干净的还是扰动的。
Same/Cross-norm evaluation: 在Table 1 中,我们总结了我们为GoogLeNet[37]防御扰动的实验结果。表格总结了两种实验。对第一种,我们对测试和训练使用同样类型的扰动。比如,我们使用 l 2 l_{2} l2范式的扰动来学习框架组件(修正器和检测器),之后也使用 l 2 l_{2} l2范式的扰动进行测试。这些实验结果展示在表格左半部分。我们在 l 2 l ∞ l_{2} l_{\infty} l2l∞范式上,对两种测试方案(在表中定义为Prot-A和Prot-B)进行"same test/train perturbation type"实验。在第二种实验中,我们在训练框架时使用一种扰动,在测试时使用另一种扰动。表格的右半部分总结了实验结果。表格中提到的扰动类型是对测试数据而言。同样的惯例在另外两个目标模型的表格上同样被使用。可视化扰动和修正图像的代表样本展示在Figure 4 中。请参考补充材料中更多的展示结果。


从Table 1 中我们可以看到,总体而言,我们的框架可以很成功的为GoogLeNet防御针对这个网络的通用对抗扰动。Prot-A展示了当攻击者可能把扰动添加到不可见的图像上,在不知道干净数据是否能被目标网络正确分类的情况下我们的框架的表现。Prot-B展示了把扰动添加到原来被分类器正确分类的图像上来愚弄网络的情况。注意的是,我们的框架对于Prot-A和Prot-B有不同的表现和目标模型在干净数据上的准确率有关。对于一个在干净数据上100%准确的网络,Prot-A和Prot-B上的结果很相似。对于准确率低的分类器有不同的结果,在子表中有证据。
在Table 2 中,我们总结了我们的框架对CaffeNet[16]的表现。再一次,结果展示了对扰动很好的防御效果。最终 l 2 l_{2} l2范式的防御效果在Prot-A上是96.4%。在使用的度量定义和实验方案下,对这一值的解释如下。通过我们的框架提供的防御包装,CaffeNet的表现达到了原始表现(干净数据完美分类)的96.4%,每张图像都有均等的机会是干净或者扰动。考虑在我们的实验中使用的所有测试扰动,网络的愚弄率至少是80%,这是一次很好的恢复表现。
在Table 3 中记录了VGG-F network[4]的总结,再一次展示了我们框架较好的表现。有趣的事,对于CaffeNet和VGG-F,在"different test/train perurtation type"情况下,测试图像上 l ∞ l_{\infty} l∞范式的扰动能够很准确的被我们的检测器检测出来。虽然如此,它不想GoogLeNet那样。我们发现,对于 l ∞ ( ξ = 10 ) l_{\infty}(\xi=10) l∞(ξ=10)范式的扰动和对应的 l 2 l_{2} l2范式的扰动而言,GoogLeNet(大约平均2400)与CaffeNet和VGG-F(大约平均2850)相比更低。这使得对于GoogLeNet的 l ∞ l_{\infty} l∞范式扰动检测更困难。这些值的差异表明,在GoogLeNet和其他的两个网络上的决策边界有明显的差异,这是被网络的显著的结构差异决定的。
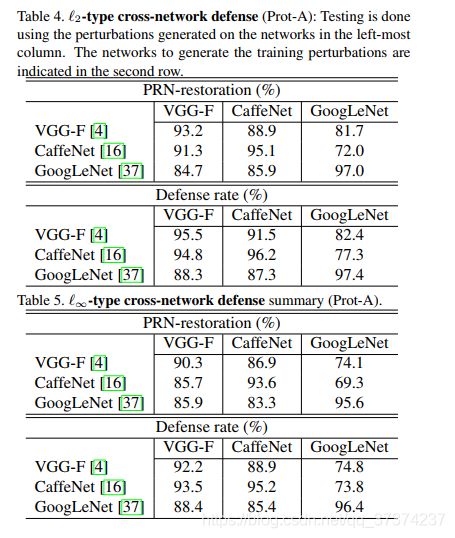
Ceoss-architecture generalisation: 通过上面的观察结果,预计我们的框架的跨网络防御性能将比类似结构的网络更好。这个预测被Table 4 Table 5 的实验结果验证。这些表格展示了我们使用""same test/train perturtation type"在 l 2 l ∞ l_{2} l_{\infty} l2l∞上的表现。结果展示了方案A的实验。对于方案B对应的实验,可以参考补充实验。从这些表格中,我们可以得出结论,我们的框架在不同的模型上有很好的泛化性,尤其是在有类似结构的网络之间。我们推测,我们的框架从通用对抗扰动的交叉模型泛化中继承了交叉网络泛化性。与我们的技术一样,任何防御这些扰动的框架都可以被期望表现出类似的特征。

6.结论
我们提出了第一个专门防御通用对抗扰动[25]的框架,不仅仅能够检测图像中的扰动,还你呢广告对扰动图像进行修正,这样目标分类器能够可靠的预测标签。提出的框架不需要修改目标模型就可以提供防御,使得我们的技术对于实际场景更加适合。另外,为了防止可能的反防御措施,它提供了保持“修正器”和“检测器”组件保密的灵活性。我们通过扰动修正网络(PRN)实现修正器,通过利用PRN的图像转移来训练SVM实现检测器。为了高效的训练,我们提出了一种计算图像无关的合成扰动的方法。我们框架的效果是通过为CaffeNet[16]VGG-F network[4]GoogLeNet[37]提供对通用对抗扰动的成功防御展现的。
知识 这个研究是通过ARC grant DP160101458支持的。用于这项研究的Titan Xp是由NVIDIA公司捐赠的。
参考文献
[1] N. Akhtar and A. Mian. Threat of adversarial attacks on deep learning in computer vision: A survey. arXiv preprint arXiv:1801.00553, 2018.
[2] S. Baluja and I. Fischer. Adversarial transformation networks: Learning to generate adversarial examples. arXiv preprint arXiv:1703.09387, 2017.
[3] N. Carlini and D. Wagner. Towards evaluating the robustness of neural networks. In Security and Privacy (SP), 2017 IEEE Symposium on, pages 39–57. IEEE, 2017.
[4] K. Chatfield, K. Simonyan, A. Vedaldi, and A. Zisserman. Return of the devil in the details: Delving deep into convolutional nets. arXiv preprint arXiv:1405.3531, 2014.
[5] G. K. Dziugaite, Z. Ghahramani, and D. M. Roy. A study of the effect of jpg compression on adversarial images. arXiv preprint arXiv:1608.00853, 2016.
[6] A. Fawzi, O. Fawzi, and P. Frossard. Analysis of classi- fiers’ robustness to adversarial perturbations. arXiv preprint arXiv:1502.02590, 2015.
[7] A. Fawzi, S.-M. Moosavi-Dezfooli, and P. Frossard. Robustness of classifiers: from adversarial to random noise. In Advances in Neural Information Processing Systems, pages 1632–1640, 2016.
[8] V. Fischer, M. C. Kumar, J. H. Metzen, and T. Brox. Adversarial examples for semantic image segmentation. arXiv preprint arXiv:1703.01101, 2017.
[9] I. Goodfellow, Y. Bengio, and A. Courville. Deep learning. 2016.
[10] I. J. Goodfellow, J. Shlens, and C. Szegedy. Explaining and harnessing adversarial examples. arXiv preprint arXiv:1412.6572, 2014.
[11] K. He, X. Zhang, S. Ren, and J. Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision, pages 1026–1034, 2015.
[12] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
[13] G. Hinton, O. Vinyals, and J. Dean. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2015.
[14] G. Huang, Z. Liu, K. Q. Weinberger, and L. van der Maaten. Densely connected convolutional networks. arXiv preprint arXiv:1608.06993, 2016.
[15] D. Kingma and J. Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
[16] A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105, 2012.
[17] A. Kurakin, I. Goodfellow, and S. Bengio. Adversarial examples in the physical world. arXiv preprint arXiv:1607.02533, 2016.
[18] A. Kurakin, I. Goodfellow, and S. Bengio. Adversarial machine learning at scale. arXiv preprint arXiv:1611.01236, 2016.
[19] Y. Liu, X. Chen, C. Liu, and D. Song. Delving into transferable adversarial examples and black-box attacks. arXiv preprint arXiv:1611.02770, 2016.
[20] J. Lu, T. Issaranon, and D. Forsyth. Safetynet: Detecting and rejecting adversarial examples robustly. arXiv preprint arXiv:1704.00103, 2017.
[21] J. Lu, H. Sibai, E. Fabry, and D. Forsyth. No need to worry about adversarial examples in object detection in autonomous vehicles. arXiv preprint arXiv:1707.03501, 2017.
[22] Y. Luo, X. Boix, G. Roig, T. Poggio, and Q. Zhao. Foveation-based mechanisms alleviate adversarial examples. arXiv preprint arXiv:1511.06292, 2015.
[23] J. H. Metzen, T. Genewein, V. Fischer, and B. Bischoff. On detecting adversarial perturbations. arXiv preprint arXiv:1702.04267, 2017.
[24] J. H. Metzen, M. C. Kumar, T. Brox, and V. Fischer. Universal adversarial perturbations against semantic image segmentation. arXiv preprint arXiv:1704.05712, 2017.
[25] S.-M. Moosavi-Dezfooli, A. Fawzi, O. Fawzi, and P. Frossard. Universal adversarial perturbations. CVPR, 2017.
[26] S.-M. Moosavi-Dezfooli, A. Fawzi, O. Fawzi, P. Frossard, and S. Soatto. Analysis of universal adversarial perturbations. arXiv preprint arXiv:1705.09554, 2017.
[27] S.-M. Moosavi-Dezfooli, A. Fawzi, and P. Frossard. Deepfool: a simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2574–2582, 2016.
[28] V. Nair and G. E. Hinton. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th international conference on machine learning (ICML-10), pages 807–814, 2010.
[29] A. Nguyen, J. Yosinski, and J. Clune. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 427–436, 2015.
[30] N. Papernot, P. McDaniel, X. Wu, S. Jha, and A. Swami. Distillation as a defense to adversarial perturbations against deep neural networks. In Security and Privacy (SP), 2016 IEEE Symposium on, pages 582–597. IEEE, 2016.
[31] A. Prakash, N. Moran, S. Garber, A. DiLillo, and J. Storer. Deflecting adversarial attacks with pixel deflection. arXiv preprint arXiv:1801.08926, 2018.
[32] A. Rozsa, E. M. Rudd, and T. E. Boult. Adversarial diversity and hard positive generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 25–32, 2016.
[33] O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, et al. Imagenet large scale visual recognition challenge. International Journal of Computer Vision, 115(3):211–252, 2015.
[34] S. Sabour, Y. Cao, F. Faghri, and D. J. Fleet. Adversarial manipulation of deep representations. arXiv preprint arXiv:1511.05122, 2015.
[35] M. Sharif, S. Bhagavatula, L. Bauer, and M. K. Reiter. Accessorize to a crime: Real and stealthy attacks on state-of-the-art face recognition. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pages 1528–1540. ACM, 2016.
[36] K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.
[37] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1–9, 2015.
[38] C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens, and Z. Wojna. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2818–2826, 2016.
[39] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, and R. Fergus. Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199, 2013.
[40] P. Tabacof and E. Valle. Exploring the space of adversarial images. In Neural Networks (IJCNN), 2016 International Joint Conference on, pages 426–433. IEEE, 2016.
[41] T. Tanay and L. Griffin. A boundary tilting persepective on the phenomenon of adversarial examples. arXiv preprint arXiv:1608.07690, 2016.
[42] F. Tramer, A. Kurakin, N. Papernot, D. Boneh, and P. Mc- ` Daniel. Ensemble adversarial training: Attacks and defenses. arXiv preprint arXiv:1705.07204, 2017.
[43] C. Xie, J. Wang, Z. Zhang, Y. Zhou, L. Xie, and A. Yuille. Adversarial examples for semantic segmentation and object detection. arXiv preprint arXiv:1703.08603, 2017.