神经网络

神经网络与深度学习

深度学习（deep learning）是机器学习拉出的分支，它试图使用包含复杂结构或由多重非线性变换构成的多个处理层对数据进行高层抽象。深度学习是机器学习中一种基于对数据进行表征学习的方法。观测值（例如一幅图像）可以使用多种方式来表示，如每个像素强度值的向量，或者更抽象地表示成一系列边、特定形状的区域等。而使用某些特定的表示方法更容易从实例中学习任务（例如，人脸识别或面部表情识别）。深度学习的好处是用非监督式的特征学习和分层特征提取高效算法来替代手工获取特征。

至今已有数种深度学习框架，如深度神经网络、卷积神经网络和深度置信网络和递归神经网络已被应用计算机视觉、语音识别、自然语言处理、音频识别与生物信息学等领域并获取了极好的效果。

神经网络，一种启发自生物学的优美的编程范式，能够从观测到的数据中进行学习

神经网络基础

感知器

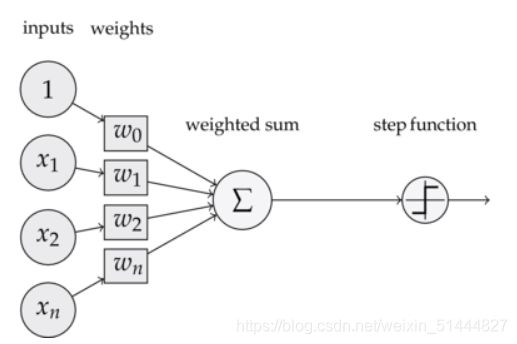
输入权值，一个感知器可以有多个输入，每个输入上有一个权值。

激活函数，感知器的激活函数有很多选择。

输出，y = f(W * x + b)----W：权重，b：偏置

应用：很容易解决与、或、非问题----分类问题。

单个感知器解决不了的问题，可以增加感知器。

人工神经网络（ANN）

定义：

在机器学习和认知科学领域，人工神经网络（artificial neural network，缩写ANN），简称神经网络（neural network，缩写NN）或类神经网络，是一种模仿生物神经网络的结构和功能的计算模型，用于对函数进行估计或近似。

神经网络的种类：

基础神经网络：单层感知器，线性神经网络，BP神经网络，Hopfield神经网络等

进阶神经网络：玻尔兹曼机，受限玻尔兹曼机，递归神经网络等

深度神经网络：深度置信网络，卷积神经网络，循环神经网络，LSTM网络等

神经网络的特点：

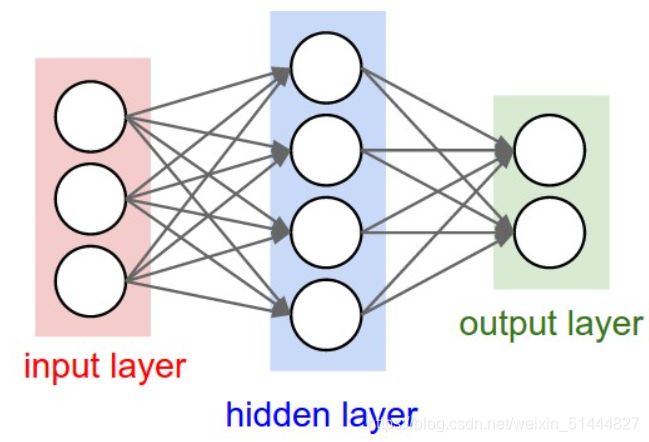
1）输入向量的维度和输入神经元的个数相同

2）每个连接都有个权值

3）同一层神经元之间没有连接

4）由输入层，隐层，输出层组成

5）第N层与第N-1层的所有神经元连接，也叫全连接

神经网络的组成：

结构（Architecture）例如，神经网络中的变量可以是神经元连接的权重

激励函数（Activity Rule）大部分神经网络模型具有一个短时间尺度的动力学规则，来定义神经元如何根据其他神经元的活动来改变自己的激励值。

学习规则（Learning Rule）学习规则指定了网络中的权重如何随着时间推进而调整。（反向传播算法）

神经网络API模块：

在使用tensorflow时候，tf.nn， tf.layers，tf.contrib模块有很多功能是重复的。

(1) tf.nn: 提供神经网络相关操作的支持，包括卷积操作(conv) 、池化操作(pooling) 、归一化、loss、分类操作、embedding、 RNN、 Evaluation。

(2) tf.layers: 主要提供高层的神经网络，主要和卷积相关的，对tf.nn的进一步封装。

(3) tf.contrib: tf.contrib.layers提供够将计算图中的网络层、正则化、摘要操作，是构建计算图的高级操作。

浅层人工神经网络模型

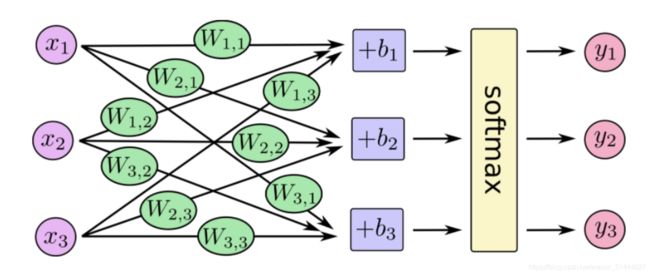
SoftMax回归

步骤：1）将输入的证据加在某些类中，然后将该证据转换成概率。2）每个输出的概率，对应着编码中具体的类别。

在神经网络中，整个过程如下(softmax模型)：

损失计算API

1）全连接-从输入直接到输出

特征加权：

tf.matmul(a, b,name=None)+bias

return:全连接结果，供交叉损失运算。不需要激活函数（因为是最后的输出）

2）SoftMax计算、交叉熵

tf.nn.softmax_cross_entropy_with_logits(labels=None, logits=None,name=None)

计算logits和labels之间的交叉熵损失，该函数包含了softmax功能。

labels:标签值（真实值）

logits：样本加权之后的值（预测值）

return:返回损失值列表

3）损失值列表平均值计算

tf.reduce_mean(input_tensor)

计算张量的尺寸的元素平均值

4）损失下降API

tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

梯度下降优化

learning_rate:学习率，一般为0-1

minimize(loss):最小化损失

return:梯度下降op

Mnist数据集神经网络分析

1）准备数据

2）全连接结果计算

3）损失优化

4）模型评估（计算准确性）

5）保存模型

6 ）重新打开模型，预测测试集

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

FLAGS = tf.app.flags.FLAGS
tf.app.flags.DEFINE_integer("is_train",1,"指定程序是预测还是训练") # 1--训练 0-预测

def full_connected():
    # 获取真实的数据
    mnist = input_data.read_data_sets("E:/PythonProject/tf/mnist/input_data/",one_hot=True)

    # 1. 建立数据的占位符  x[None,784]   y_true[None,10]
    with tf.variable_scope("data"):
        x = tf.placeholder(tf.float32,[None,784])
        y_true = tf.placeholder(tf.int32,[None,10])
        
    # 2.建立一个全连接层的神经网络 w[784,10]  b[10]
    with tf.variable_scope("fc_model"):
        # 随机初始化权重和偏置
        weight = tf.Variable(tf.random_normal([784,10],mean=0.0,stddev=1.0),name="weight")
        bias = tf.Variable(tf.constant(0.0,shape=[10]))
        # 预测None个样本的输出结果
        y_predict = tf.matmul(x,weight) + bias
        
    # 3.求出所有样本的损失，求平均值
    with tf.variable_scope("soft_cross"):
        # 求平均交叉熵损失
        loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_true,logits=y_predict))

    # 4.梯度下降求出损失
    with tf.variable_scope("optimizer"):
        train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

    # 5.计算准确率
    with tf.variable_scope("acc"):
        equal_list = tf.equal(tf.arg_max(y_true,1),tf.arg_max(y_predict,1))
        # equal_list None个样本 [1,0,1,,1,1,0,1,0,1,1......]
        accuracy = tf.reduce_mean(tf.cast(equal_list,tf.float32))

    # 收集变量  单个数字值收集
    tf.summary.scalar("losses",loss)
    tf.summary.scalar("acc",accuracy)
    # 高纬度变量收集
    tf.summary.histogram("weights",weight)
    tf.summary.histogram("biases",bias)
     # 定义一个初始化变量的op
    init_op = tf.global_variables_initializer()
    # 定义一个合并变量的op
    merged = tf.summary.merge_all()

    # 创建一个saver
    saver = tf.train.Saver()

    # 开启会话训练
    with tf.Session() as sess:
        # 初始化变量
        sess.run(init_op)
        # 建立events文件，然后写入
        filewriter = tf.summary.FileWriter("E:/PythonProject/tf/test/",graph=sess.graph)

        if FLAGS.is_train == 1:

            # 迭代步数去训练，更新参数预测
            for i in range(2000):
                # 取出真实存在的特征值和目标值
                mnist_x,mnist_y = mnist.train.next_batch(50)
                # 运行train_op训练
                sess.run(train_op,feed_dict={x:mnist_x,y_true:mnist_y})
                # 写入每步变量的值
                summary = sess.run(merged,feed_dict={x:mnist_x,y_true:mnist_y})
                filewriter.add_summary(summary,i)
                print("训练第%d步，准确率为：%f" % (i,sess.run(accuracy,feed_dict={x:mnist_x,y_true:mnist_y})))
            # 保存模型
            saver.save(sess,"E:/PythonProject/tf/tmp/fc_model")
        else:
            # 加载模型
            saver.restore(sess,"E:/PythonProject/tf/tmp/fc_model")
            # 如果是0，做出预测
            for i in range(100):
                # 每次测试一张图片
                x_test,y_test = mnist.test.next_batch(1)
                print("第%d张图片，手写数字目标是：%d，预测结果是:%d" %(
                    i,
                    tf.argmax(y_test,1).eval(),
                    tf.argmax(sess.run(y_predict,feed_dict={x:x_test,y_true:y_test}),1).eval()
                ))

    return None


if __name__ == '__main__':
    full_connected()

卷积神经网络（CNN）

1）人工神经网络VS卷积神经网络

人工神经网络之所以不太适合图像识别任务，主要有以下几个方面的问题：

1.1）参数数量太多，在CIFAR-10（一个比赛数据集）中，图像大小为32x32x3（32宽，32高，3色通道），因此在正常神经网络的第一隐藏层中的单个完全连接的神经元将具有32 * 32 * 3 = 3072个权重。这个数量仍然是可控的，但显然这个完全连接的结构不会扩大到更大的图像。例如，一个更可观的大小的图像，例如200x200x3，会导致具有200 * 200 * 3 = 120000重量的神经元。此外，我们几乎肯定会有几个这样的神经元，所以参数会加快！显然，这种完全连接是浪费的，而且大量的参数会很快导致过度配套。

1.2）没有利用像素之间的位置信息。对于图像识别任务来说，每个像素和其周围像素的联系是比较紧密的，和离得很远的像素的联系可能就很小了。如果一个神经元和上一层所有神经元相连，那么就相当于对于一个像素来说，把图像的所有像素都等同看待，这不符合前面的假设。当我们完成每个连接权重的学习之后，最终可能会发现，有大量的权重，它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重，这样的学习必将是非常低效的。

1.3）网络层数限制。网络层数越多其表达能力越强，但是通过梯度下降方法训练深度人工神经网络很困难，因为全连接神经网络的梯度很难传递超过3层。因此，我们不可能得到一个很深的全连接神经网络，也就限制了它的能力。

那么，卷积神经网络又是怎样解决这个问题的呢？主要有三个思路：

1.4）局部连接。这个是最容易想到的，每个神经元不再和上一层的所有神经元相连，而只和一小部分神经元相连。这样就减少了很多参数。

1.5）权值共享。一组连接可以共享同一个权重，而不是每个连接有一个不同的权重，这样又减少了很多参数。

1.6）下采样。可以使用Pooling来减少每层的样本数，进一步减少参数数量，同时还可以提升模型的鲁棒性。对于图像识别任务来说，卷积神经网络通过尽可能保留重要的参数，去掉大量不重要的参数，来达到更好的学习效果。

2）深层的神经网络：

深度学习网络与更常见的单一隐藏层神经网络的区别在于深度。深度学习网络中，每一个节点层在前一层输出的基础上学习识别一组特定的特征。随着神经网络深度增加，节点所能识别的特征也就越来越复杂。

3）卷积神经网络的发展历史

4）卷积神经网络的结构分析

神经网络(neural networks)的基本组成包括输入层、隐藏层、输出层。而卷积神经网络的特点在于隐藏层分为卷积层和池化层(pooling layer，又叫下采样层)。

卷积层：通过在原始图像上平移来提取特征，每一个特征就是一个特征映射。功能是定义过滤器（观察窗口）—即“权重”，与像素线性回归。

四个超参数：1）过滤器个数 2）过滤器大小 3）步长 4）零填充

得到的每一个深度也叫一个Feature Map。

卷积层输出深度：由过滤器个数决定

卷积层输出宽度：

输入体积大小：H1 * W1 * D1

四个超参数：

1）Filter数量K 2）Filter大小F 3）步长S 4）零填充大小P

输出体积大小：H2 * W2 * D2

H2 = (H1 - F + 2P)/S + 1

W2 = (W1 - F + 2P)/S + 1

D2 = K

卷积层的零填充:

卷积核在提取特征映射时的动作称之为padding（零填充），由于移动步长不一定能整出整张图的像素宽度。其中有两种取样方式，SAME和VALID

SAME：越过边缘取样，取样的面积和输入图像的像素宽度一致。

VALID：不越过边缘取样，取样的面积小于输入人的图像的像素宽度

卷积层API：

tf.nn.conv2d(input, filter, strides=, padding=, name=None)

计算给定4-D input和filter张量的2维卷积

input：给定的输入张量，具有[batch,heigth,width,channel]，类型为float32,64

filter：指定过滤器的大小，[filter_height, filter_width,in_channels, out_channels]

strides：strides = [1, stride, stride, 1]，步长

padding：“SAME”, “VALID”，使用的填充算法的类型，使用“SAME”。其中”VALID”表示滑动超出部分舍弃，“SAME”表示填充，使得变化后height,width一样大

激活函数：

增加激活函数：能增加网络的非线性分割能力

Relu：f(x) = max(0，x)

激活函数API：

tf.nn.relu(features, name=None)

features:卷积后加上偏置的结果

return:结果

sigmoid函数的缺点：

第一，采用sigmoid等函数，反向传播求误差梯度时，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多

第二，对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度爆炸的情况（求不出权重和偏置）

池化层：通过特征后稀疏参数来减少学习的参数，降低网络的复杂度。（最大池化和平均池化）Pooling层主要的作用是特征提取，通过去掉Feature Map中不重要的样本，进一步减少参数数量。Pooling的方法很多，最常用的是Max Pooling。

池化API：

tf.nn.max_pool(value, ksize=, strides=, padding=,name=None)

输入上执行最大池数

value:4-D Tensor形状[batch, height, width, channels]

ksize:池化窗口大小，[1, ksize, ksize, 1]

strides:步长大小，[1,strides,strides,1]

padding:“SAME”, “VALID”，使用的填充算法的类型，使用“SAME”

全连接层：

前面的卷积和池化相当于做特征工程，后面的全连接相当于做特征加权。最后的全连接层在整个卷积神经网络中起到“分类器”的作用。

Mnist手写数字图片识别卷积网络案例

Mnist数据集可以从官网下载，网址： http://yann.lecun.com/exdb/mnist/ 下载下来的数据集被分成两部分：55000行的训练数据集（mnist.train）和10000行的测试数据集（mnist.test）。每一个MNIST数据单元有两部分组成：一张包含手写数字的图片和一个对应的标签。我们把这些图片设为“xs”，把这些标签设为“ys”。训练数据集和测试数据集都包含xs和ys，比如训练数据集的图片是 mnist.train.images ，训练数据集的标签是 mnist.train.labels。

我们可以知道图片是黑白图片，每一张图片包含28像素X28像素。我们把这个数组展开成一个向量，长度是 28x28 = 784。因此，在MNIST训练数据集中，mnist.train.images 是一个形状为 [60000, 784] 的张量。

MNIST中的每个图像都具有相应的标签，0到9之间的数字表示图像中绘制的数字。用的是one-hot编码。

1）准备数据

2）卷积、激活、池化（两层）

3）全连接层

4）计算准确率

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'


# 定义一个初始化权重的函数
def weight_variables(shape):
    w = tf.Variable(tf.random_normal(shape=shape,mean=0.0,stddev=1.0))
    return w

# 定义一个初始化偏置的函数
def bias_variables(shape):
    b = tf.Variable(tf.constant(0.0,shape=shape))
    return b

def model():
    """
    自定义的卷积模型
    :return:
    """
    # 1. 建立数据的占位符  x[None,784]   y_true[None,10]
    with tf.variable_scope("data"):
        x = tf.placeholder(tf.float32, [None, 784])
        y_true = tf.placeholder(tf.int32, [None, 10])
    # 2.一卷积层 卷积 5*5*1 32个 步长 = 1、激活 tf.nn.relu()、池化
    with tf.variable_scope("conv1"):
        # 随机初始化过滤器（权重）/偏置[32]
        w_conv1 = weight_variables([5,5,1,32])
        b_conv1 = bias_variables([32])
        # 对x进行形状的改变[None,784] -- [None,28,28,1]
        x_reshape = tf.reshape(x,[-1,28,28,1])
        # [None,28,28,1] ---- [None,28,28,32]
        x_relu1 = tf.nn.relu(tf.nn.conv2d(x_reshape,w_conv1,strides=[1,1,1,1],padding="SAME") + b_conv1)
        # 池化 2*2 strides 2 [None,28,28,32]----[None,14,14,32]
        x_pool1 = tf.nn.max_pool(x_relu1,ksize=[1,2,2,1],strides=[1,2,2,1],padding="SAME")
    # 3.二卷积层 5*5*32  64个filter  步长 = 1 激活：tf.nn.relu 池化：
    with tf.variable_scope("conv2"):
        # 随机初始化权重 权重[5,5,32,64] 偏置[64]
        w_conv2 = weight_variables([5,5,32,64])
        b_conv2 = bias_variables([64])
        # 卷积、激活、池化计算
        # [None,14,14,32] ---- [None,14,14,64]
        x_relu2 = tf.nn.relu(tf.nn.conv2d(x_pool1,w_conv2,strides=[1,1,1,1],padding="SAME") + b_conv2)
        # 池化 2*2 strides 2 ,[None,14,14,64]----[None,7,7,64]
        x_pool2 = tf.nn.max_pool(x_relu2,ksize=[1,2,2,1],strides=[1,2,2,1],padding="SAME")
    # 4.全连接层 [None,7,7,64] --- [None,7*7*64] * [7*7*64,10] + [10] = [None,10]
    with tf.variable_scope("fc"):
        # 随机初始化权重和偏置
        w_fc = weight_variables([7*7*64,10])
        b_fc = bias_variables([10])
        # 修改形状 [None,7,7,64] ---[None,7*7*64]
        x_fc_reshape = tf.reshape(x_pool2,[-1,7*7*64])
        # 进行矩阵运算得出每个样本的10个结果
        y_predict = tf.matmul(x_fc_reshape,w_fc) + b_fc

        return x,y_true,y_predict

def conv_fc():
    # 获取真实的数据
    mnist = input_data.read_data_sets("E:/PythonProject/tf/mnist/input_data/", one_hot=True)
    # 定义模型，得出输出
    x,y_true,y_predict = model()
    # 进行交叉熵损失计算

    # 求出所有样本的损失，求平均值
    with tf.variable_scope("soft_cross"):
        # 求平均交叉熵损失
        loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_true, logits=y_predict))
    # 梯度下降求出损失
    with tf.variable_scope("optimizer"):
        train_op = tf.train.GradientDescentOptimizer(0.01).minimize(loss)
    # 计算准确率
    with tf.variable_scope("acc"):
        equal_list = tf.equal(tf.arg_max(y_true, 1), tf.arg_max(y_predict, 1))
        # equal_list None个样本 [1,0,1,,1,1,0,1,0,1,1......]
        accuracy = tf.reduce_mean(tf.cast(equal_list, tf.float32))

    # 定义一个初始化变量的op
    init_op = tf.global_variables_initializer()

    # 开启会话运行
    with tf.Session() as sess:
        sess.run(init_op)

        # 循环去训练
        for i in range(1000):
            # 取出真实存在的特征值和目标值
            mnist_x,mnist_y = mnist.train.next_batch(50)
            # 进行train_op 训练
            sess.run(train_op,feed_dict={x:mnist_x,y_true:mnist_y})

            print("训练第%d步,准确率为:%f" % (i, sess.run(accuracy, feed_dict={x: mnist_x, y_true: mnist_y})))

    return None

if __name__ == "__main__":
    conv_fc()