学习笔记 —— 吴恩达《机器学习》课程
目录
- 一、前言
-
- 1.1 监督学习:
- 1.2 无监督学习
- 二、线性回归
-
- 2.1 代价函数
- 2.2 梯度下降算法
- 三、矩阵和向量
- 四、多元线性回归
-
- 4.1 特征缩放
- 4.2 学习率α
- 4.4 特征和多项式
- 4.4 正规方程
- 五、Octave教程(Octave Tutorial)
- 六、逻辑回归
-
- 6.1 Sigmoid 函数
- 6.2 决策边界
-
- 6.2.1 线性决策边界
- 6.2.2 非线性决策边界
- 6.3 代价函数
- 6.4 高级优化
- 6.5 多类别分类
- 七、 正则化
-
- 7.1 过拟合问题
- 7.2 代价函数
- 7.3 线性回归的正则化
- 7.4 logistic回归的正则化
- 八、神经网络:表述
-
- 8.1 非线性假设
- 8.2 神经元和大脑
- 8.3 神经网络举例
- 8.4 多元分类问题
- 九、神经网络的学习
-
- 9.1 代价函数
- 9.2 反向传播算法
- 9.3 理解反向传播
- 9.4 梯度检验
- 9.5 随机初始化
- 9.6 总体回顾
- 9.7 神经网络举例:无人驾驶
- 十、应用机器学习的建议
-
- 10.1 决定下一步做什么
- 10.2 评估假设
- 10.3 模型选择和交叉验证集
- 10.4 诊断偏差与方差
- 10.5 正则化和偏差、方差
- 10.6 学习曲线
- 10.7 决定下一步做什么
- 十一、机器学习系统的设计
-
- 11.1 首先要做什么
- 11.2 误差分析
- 11.3 不对称性分类得误差评估
- 11.4 查准率和召回率的权衡
- 11.5 机器学习数据
- 十二、支持向量机
-
- 12.1 优化目标
- 12.2 大边界的直观理解
- 12.3 数学背后的大边界分类
- 12.4 (高斯)核函数1
- 12.5 (高斯)核函数2
- 12.6 使用支持向量机
- 十三、聚类
-
- 13.1 无监督学习
- 13.2 K-Means算法
- 13.3 优化目标
- 13.4 随机初始化
- 13.5 选择聚类数
- 十四、降维
-
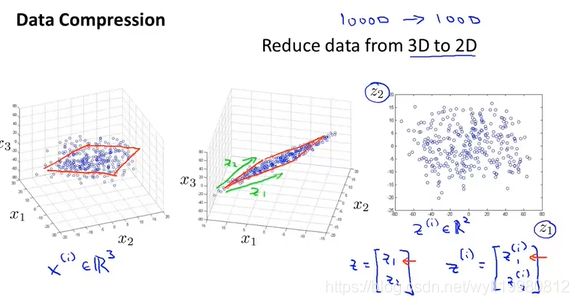
- 14.1 应用一:数据压缩
- 14.2 应用二:数据可视化
- 14.3 主成分分析PCA
- 14.4 重建的压缩表示
- 14.5 选择主成分的数量
- 14.6 主成分分析的应用建议
- 十五、异常检测
-
- 15.1 问题的动机
- 15.2 高斯分布
- 15.3 算法
- 15.4 开发和评价一个异常检测系统
- 15.5 异常检测 VS 监督学习
- 15.6 选择特征
- 15.7 多元高斯分布
- 15.8 使用多元高斯分布进行异常检测
- 十六、推荐系统
-
- 16.1 问题形式化
- 16.2 基于内容的推荐系统
- 16.3 协同过滤
- 16.4 协同过滤算法
- 16.5 向量化实现
- 16.6 均值归一化
- 十七、大规模机器学习
-
- 17.1 大型数据集的学习
- 17.2 随机梯度下降法
- 17.3 随机梯度下降收敛
- 17.4 小批量梯度下降
- 17.5 在线学习
- 17.6 映射化简和数据并行
- 十八、应用实例:图片文字识别OCR
-
- 18.1 问题描述和流程图
- 18.2 滑动窗口
- 18.3 获取大量数据和人工数据
- 18.4 上限分析:下一步工作
- 总结
一、前言
1.1 监督学习:
本节问题:
- 什么是监督学习、无监督学习?
监督学习:给出数据集和正确答案,要求机器给出更多的正确答案(实现预测)
离散数据问题 && 分类问题
单个 or 多个 特征/属性
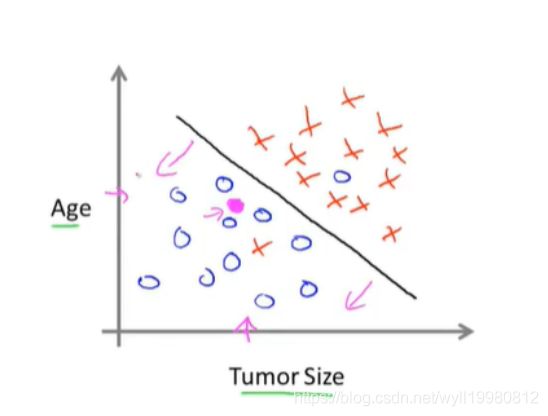
特征:年龄、肿瘤尺寸;
1.2 无监督学习

将数据集分簇 -> 聚类算法,聚类算法只是无监督算法中的一种;
无监督学习:给定数据集,但没有给出正确答案,要求机器对其分类,我们并不知道这个数据集有多少类, 看机器把它们分成多少个簇;
鸡尾酒会算法:一个酒会中两个人同时讲话,鸡尾酒会算法能将两个混合的声音分离成两个人各自的声音;
[w,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x');
~~~~~~ octave编程环境 or matlab,使用octave能够更快上手,使用c++、java则需要更复杂的代码(链接到库等等);一般,在octave中建立算法原型,待成熟后迁移到C++、Java或其它编译环境中;作为开发者,时间是最重要的;
二、线性回归
本节问题:
- 什么是线性回归?
2.1 代价函数
本节问题:
- 什么是代价函数?
- 为什么要最小化代价函数?
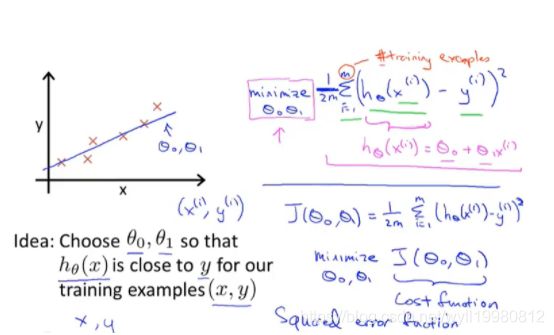
代价函数:Cost Function,又称平方误差代价函数;对偏离真实值的输出给予较大的惩罚,其大小反映了拟合函数的精准度,值越小,精准度越高,误差越小;
最小化问题:目的是找到合适的θ0、θ1,使得 hθ(x) 和 y 之间的差异小,即尽量较少假设的输出(估计值)与房子真实价格(真实值)之间的差的平方;
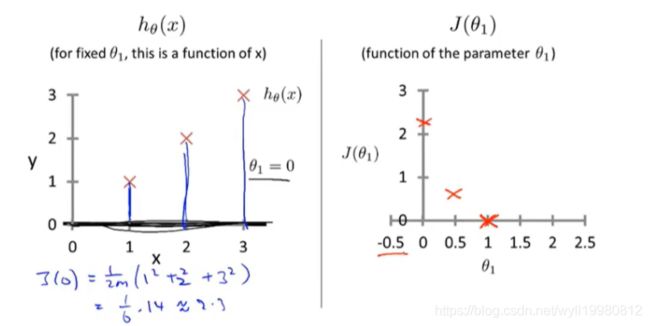
简化版的线性回归:
θ0=0,保留θ1这一个参数;
~~~~~~ 简化参数后,很容易看出:代价函数值越小,其对应的θ1所确定的直线就越接近原曲线,拟合程度就越高;
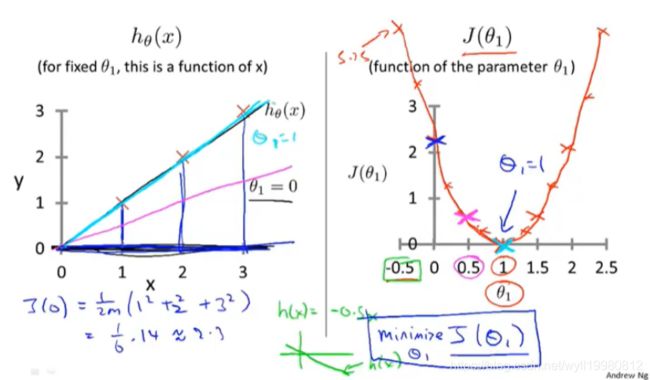
Q:那么回到两个参数的线性回归中,又该如何确定?
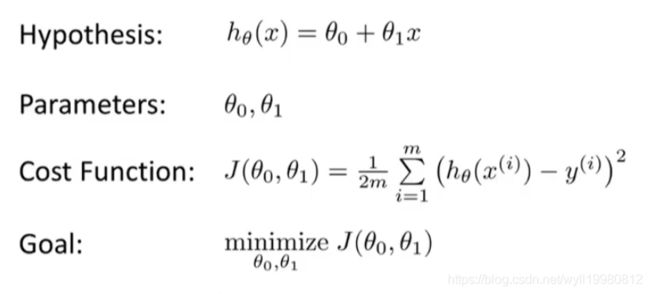
两个模型参数,则可能得到以下代价函数取值图形:

因为两个θ才能确定一个代价,不过和一个参数一样,它们都是碗状的;
将3D图转化为等高线图展示:

~~~~~~ 位于同一等高线的两点有着相同的代价函数值;想象这是一个碗,碗的底部就是这些椭圆的中心,由底部开始生长出碗,越外围,代价函数值越大;
~~~~~~ 左边的图为 (800,-0.15) 对应的拟合直线,它并没有很好地拟合直线,因为它的代价函数值很大,距离碗底还很远;
~~~~~~ 反观我们的目的就是设计出这样一种算法,它能够自动找出代价函数的最低点,那么就能得到θ0和θ1,从而确定拟合程度最好的拟合曲线,从而达到预测效果;下面就说如何设计这种算法!
2.2 梯度下降算法
本节问题:
- 什么是梯度下降法?
- 其运行机理,以及它的参数有什么作用
梯度下降:Gradient descent,不仅适用于最小化线性回归中的代价函数J(θ),还适用于其它很多领域,能够最小化很多函数;
![]()

~~~~~~ 从不同的初始位置下山,找到的却是不同的局部最优解,这是梯度下降的一大特点;

学习率α:即下一步跨的幅度,学习率越大,跨得越大,同样精确度也会随之降低,容易陷入局部最优解;
下面开始解释公式中的 导数项/偏导数:

挺容易理解的,两边都是往谷底靠;
如果α太小,就需要一小步一小步地接近谷底;
如果α太大,就可能越过最低点(代价函数变得更糟),甚至可能无法收敛;
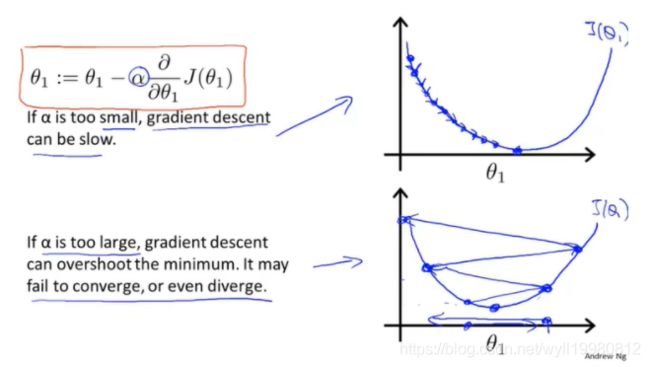
当它已经处在局部最优点时,它会一直保持在这个位置,因为后面导数项为 0,α*0=0;


~~~~~~ 梯度下降的方式:越接近最低点,|斜率|越小,导数项也就越小,每次移动的步伐就会变小;所以,无需降低α的值来控制步伐;

不断重复直到收敛;
线性回归的代价函数总是一个弓状函数 – 凸函数 convex function;
Q:为什么向下凹进去的函数反而叫凸函数?
~~~~~~ 不同的视角会看见不同的形状,从上向下看,这是个凸的,而从下往上看,这又是个凹的;因为卓里奇是北半球人,我们也是北半球人,所以我们采用卓里奇的定义(上凸函数是凹函数,下凸函数是凸函数),而我们的课本往往采用相反的定义,可能是为了与汉字形状保持一致,容易直观理解;
Batch Gradient Descent:梯度下降的每一步都使用所有的训练样本(全览整个数据集)
三、矩阵和向量
向量是特殊的矩阵;
通常:大写字母表示矩阵;小写字母表示向量或其他数字;

标量运算
矢量运算

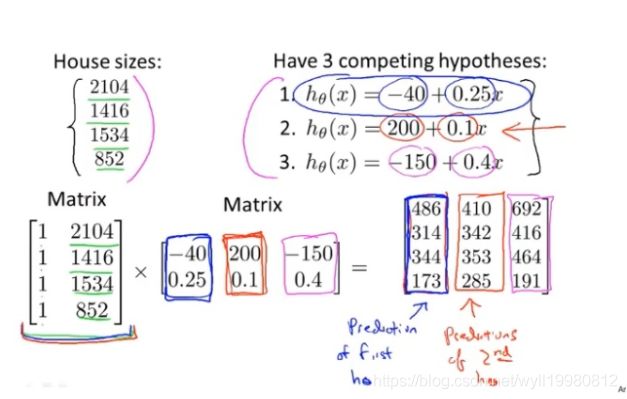
多个代价函数
矩阵的交换律不成立,但是AI = IA(I单位矩阵)
存在逆矩阵的矩阵:非奇异矩阵;
不存在逆矩阵的矩阵:奇异矩阵,比如零矩阵;

矩阵转置
四、多元线性回归
4.1 特征缩放
本节问题:
- 为什么要进行特征缩放?
- 哪种情况下进行特征缩放?其原理是什么
特征缩放:Feature Scaling,对模型特征的数量级进行放大缩小,使之都在相近或者同一数量级上;
Q:为什么要引入特征缩放?
~~~~~~ 对于有两个特征的房价预测模型,特征1是房屋大小,特征2是卧室数量,房屋大小可能几百平方米,而卧室数量只有几个,二者的数量级不在一个等级,因此对于特征1如果要梯度下降的话,需要移动很多步,或者沿着很复杂的路径,需要很多时间,最后画出来的代价函数等值线的偏移会很大(很扁的椭圆);

~~~~~~ 通过特征缩放,将两个特征的量级置于同一等级,范围一般控制在 [0,1] 或者 [-1,1] ;
~~~~~~ 特征缩放适用于数量等级差别大的特征,如果相差不大,比如0<= x1 <=3,-2<= x2 <=0.5,那么就不用考虑缩放,梯度下降法会正常地工作;如果再来个特征-100<= x3 <=100 或者 -0.0001<= x4 <=0.0001,那就要进行缩放了;

均值归一化:Mean normalization,对特征值采取 (值-均值)/(最大值) 的动作,从而使各特征的数量级处于相近水平;

特征缩放并不要求精确缩放,只是为了让梯度下降的速度更快一点而已;
4.2 学习率α
1、梯度下降算法正确运行的情况
~~~~~~ 迭代次数越多 -> 代价函数值越小 -> 代价函数减小得越慢 -> 最终收敛;
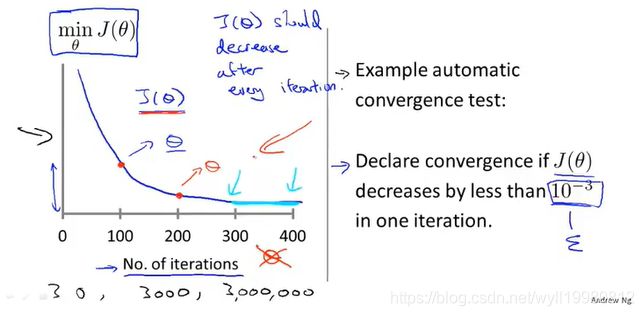
~~~~~~ 不同的问题,其收敛所需要的迭代次数都不相同,可以通过自动收敛测试(automatic convergence test)来测试到达第n此迭代时,代价函数接近收敛;原理就是设置一个阈值p,当下一步迭代的代价函数值与上一步迭代的代价函数值之差小于这个阈值p时,说明收敛;Jθ( iteration (n+1) ) - Jθ( iteration (n) ) < p;
~~~~~~ 但由于阈值p难以确定,通常不建议使用这种方法,还是通过 代价函数值-迭代次数 曲线图来判断比较直接;
2、梯度下降算法运行错误的情况:

~~~~~~ 若曲线上升,则说明过大的学习率使得每一步幅度太大,导致代价函数发散;进一步降低学习率后,发现曲线时升时降,那么还是说明学习率较大,应进一步降低;
~~~~~~ 实验证明,只要学习率α足够小,那么就能保证每一次迭代都会导致代价函数值下降;但过小的α带来高准确性的同时,也会导致收敛缓慢,大大增加运行时间;所以,选择合适的学习率对于梯度下降算法很重要;
Q:如何选择合适的学习率α?
~~~~~~ 按一定的规律不断尝试α,比如0.001, 0.003, 0.01, 0.03, 0.1, 0.3,1 .....,通过做 不同学习率的迭代次数-代价函数值图像来比较选择;
4.4 特征和多项式
本节问题:
- 为什么要定义新的特征?
- 新的特征一定好吗?
- 为什么要有多项式的转换?
定义新的特征:
~~~~~~ 比如,房价预测中特征1为房屋所占土地长,特征2为房屋所占土地宽,那么hθ(x)=θ0+θ1x1+θ2x2;如果没有对长或者宽有特殊的要求,那么我们可以将两个特征转换为1个特征 -> 面积 s=x1 * x2,这样就把二元转换成了一元;
~~~~~~ 有时候定义一个新的特征可以得到更好的模型,而有时候却不这样;以上面模型为例,当定义面积这个特征后,我们发现:不同的长宽可以得到相同的面积,那么价格也一样,那一个长10m2宽10m2的房子和一个长100m2宽1m2的房子,它们俩价格能一样吗?
~~~~~~ 所以,是否定义一个新的特征应根据实际情况、模型要求做出调整,调整得好才能达到优化模型的效果;
多项式回归 -> 多元线性回归:
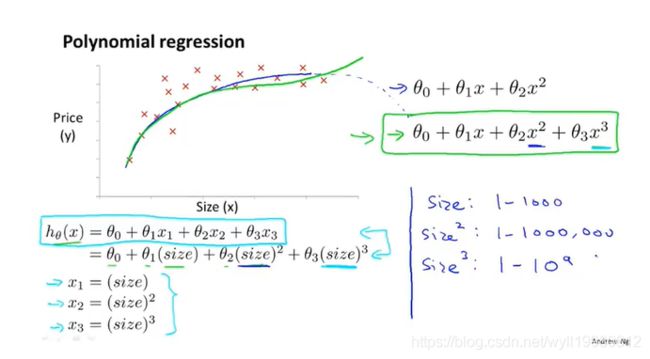
~~~~~~ 根据函数的了解和数据的走势,确定合适的多项式很重要,这里如何选择二次多项式,那么在后面是一个下降的趋势,是凸的,而房价不可能随着房屋尺寸变大而降低,所以不能选二次多项式;
~~~~~~ 将多项式转换为多元一次方程式,也要考虑特征缩放,因为特征量级发生了变化;
~~~~~~ 通过对平方根函数的了解,我认为它更适用于这个模型,因为它后面是一个上升缓慢的趋势,与数据的走势吻合度较高; h θ ( x ) = θ 0 + θ 1 ( size ) + θ 2 ( size ) h_{\theta}(x)=\theta_{0}+\theta_{1}(\text {size})+\theta_{2} \sqrt{(\text {size})} hθ(x)=θ0+θ1(size)+θ2(size)
4.4 正规方程
正规方程:Normal Eqution,通过导数值为零的点为原函数最小值(不考虑最大值)这一原理从而直接找到代价损失函数J(θ)的最小值,从而确定θ;
~~~~~~ 不需要多次迭代,一步就能走到代价函数的最小点;原理是基于函数的求导,比如一元二次函数的导数为0的点即为最小点,对于多元函数就求偏导;
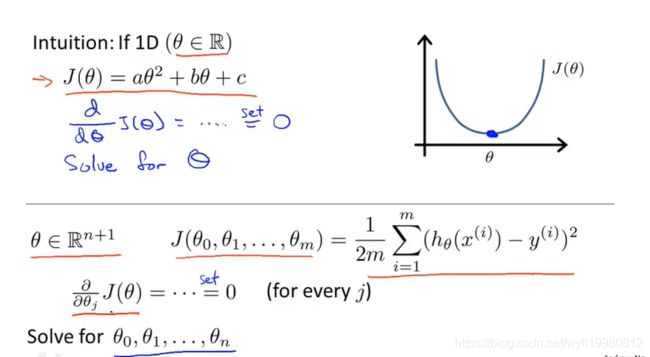

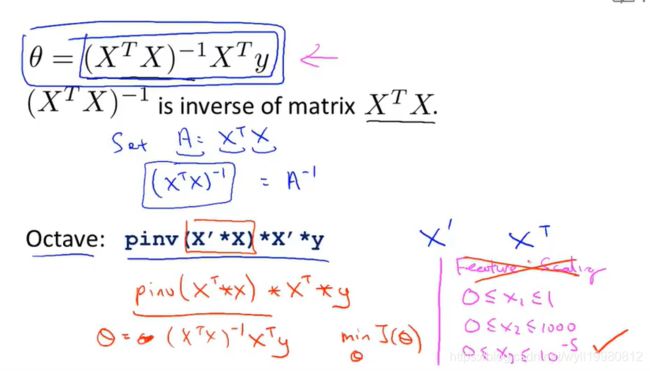
~~~~~~ 对于正规方程的推导,吴恩达老师并未给出详细的解释,只是说这个方程能求出最小的θ;此外,使用正规方程不需要考虑特征缩放,这是一大优点;
在网上搜了一下正规方程的推导过程,总结如下:
首先代价函数如下:
J ( θ ) = ∑ i = 1 n ( y i − y i ′ ) 2 = ∑ i = 1 n ( y i − h θ ( x i ) ) 2 = ( y − h θ ( X ) ) T ∗ ( y − h θ ( X ) ) J_{(\theta)}=\sum_{i=1}^{n}\left(y_{i}-y_{i}^{\prime}\right)^{2}=\sum_{i=1}^{n}\left(y_{i}-h_{\theta}\left(x_{i}\right)\right)^{2}=(y-h_{\theta}(X))^{T} *(y-h_{\theta}(X)) J(θ)=i=1∑n(yi−yi′)2=i=1∑n(yi−hθ(xi))2=(y−hθ(X))T∗(y−hθ(X))
因为
h θ ( X ) = θ ∗ X h_{\theta}(X)=\theta * X hθ(X)=θ∗X
所以
J ( θ ) = ( y − X ∗ θ ) T ∗ ( y − X ∗ θ ) J_{(\theta)}=(y-X * \theta)^{T} *(y-X * \theta) J(θ)=(y−X∗θ)T∗(y−X∗θ)
我们要得到J(θ)最小值多对应的θ,那么就要上面这个公式就要对θ求导,令其导数值为0;
矩阵求导是这样的:
d A B d B = A T \frac{d A B}{d B}=A^{T} dBdAB=AT
d X T A X d X = 2 A X \frac{d X^{T} A X}{d X}=2 A X dXdXTAX=2AX
那么我们对θ求导后得出:
d d ( θ ) ( y − X ∗ θ ) T ∗ ( y − X ∗ θ ) = 2 X T ∗ ( y − X ∗ θ ) = 0 \frac{d}{d(\theta)}(y-X * \theta)^{T} *(y-X * \theta)=2 X^{T} *(y-X * \theta)=0 d(θ)d(y−X∗θ)T∗(y−X∗θ)=2XT∗(y−X∗θ)=0
展开后得到:
2 X T ∗ y = 2 ∗ X T ∗ X ∗ θ 2 X^{T} * y=2 * X^{T} * X * \theta 2XT∗y=2∗XT∗X∗θ
那么:
θ = ( X T ∗ X ) − 1 ∗ X T ∗ y \theta=\left(X^{T} * X\right)^{-1} * X^{T} * y θ=(XT∗X)−1∗XT∗y
这个θ即对应最小的代价函数值J(θ);
类似于牛顿迭代格式 :
x~k+1~=x~k~-f(x~k~)/f‘(x~k~)
梯度下降法VS正规函数:
| 梯度下降 | 正规函数 | |
|---|---|---|
| 学习率α | 需要选择 | 不需要 |
| 迭代次数 | 需要很多次 | 一次到位,不用考虑迭代次数 |
| 特征缩放 | 需要考虑 | 不需要 |
| 数据量大时 | 当数据上万时,表现较好 | (XTX)-1使得时间复杂度为O(n3),万以下的数据现代计算机还是能很快得出结果 |
~~~~~~ 所以,对于上万级别的数据量,我们要考量两者了,看是否选择梯度下降法,而万以下的数据量,毫无疑问我们会选择正规函数,基于它有众多的优点;
五、Octave教程(Octave Tutorial)
略过;
六、逻辑回归
逻辑回归:Logistic Regression,一种广义的线性回归,其因变量可以是二分类的;
~~~~~~ 如果直接对二分类问题应用线性回归,效果并不理想,因为线性回归输出的是离散值,而不是一个用于分类的0,1值;

~~~~~~ 二分类问题的结果只可能有两种,y=0 or 1,而我们线性回归的hθ(x)能够取到一些无法确定的值,比如>1 or <0;所以,必须要有一个以用于二分类问题的 Logistic 回归算法,使hθ(x)的取值在 [0,1] 中,Logistic算法专门用于解决分类问题;
6.1 Sigmoid 函数
使用Sigmoid函数将hθ(x)输出的离散值转化成 [0,1] 范围;
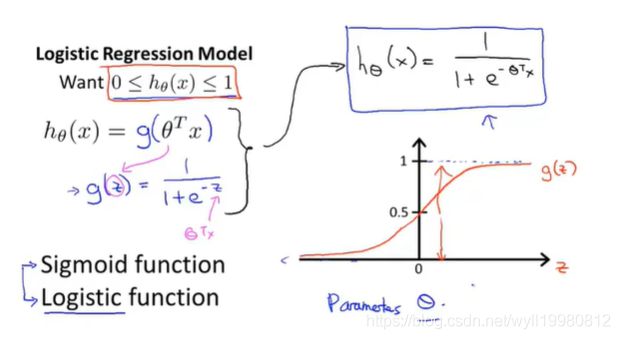

6.2 决策边界
6.2.1 线性决策边界
Decision Boundary
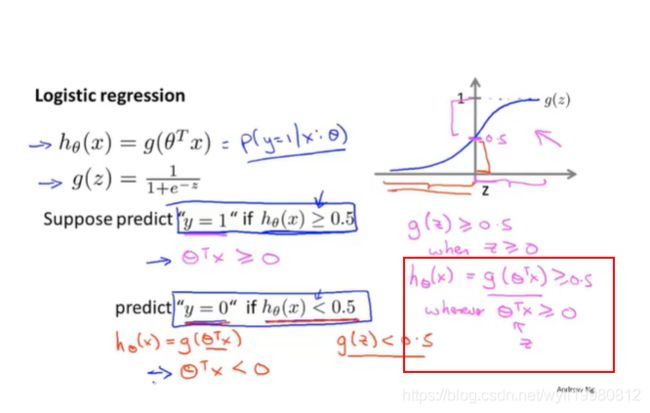
只要θTx>=0,即x0+θ1x1+θ2x2>=0,那么hθ(x)>=0.5;

6.2.2 非线性决策边界
6.3 代价函数
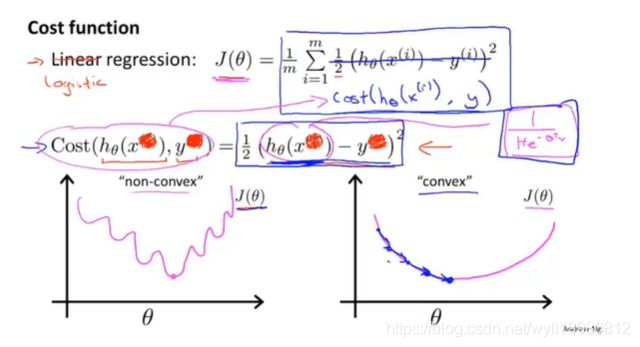
~~~~~~ 逻辑回归的代价函数和线性回归的有所不同,因为它由sigmoid函数,是一个非线性函数,所以会遇到很多个局部最优解;
引入逻辑回归中代价函数的惩罚机制;

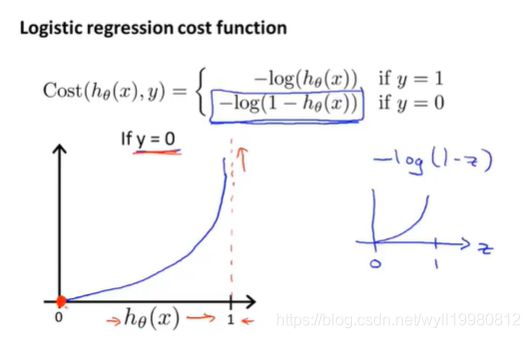
这是一个样本的惩罚,而cost函数返回每个样本平均得到的惩罚,它会是一个凸函数,不存在局部最优解;
简化代价函数与梯度下降:
对分段函数做出变换:

这个代价函数是从统计学中的极大似然法中得到的,它是凸函数,一般会选择它作为逻辑回归的代价函数;

6.4 高级优化
- Conjugate gradient
- BFGS
- L-BFGS
不需要选择学习率;收敛速度远快于梯度下降;同时也更复杂;
6.5 多类别分类
一对多的分类算法;
多分类 -> 多个二分类;
![]()
每个分类器都针对其中的一种情况进行训练;
比如:


~~~~~~ 最后输入x,选择三个分类器中可信度最高,效果最好的那个分类器,无论i值为多少我们都能得到一个较好的值,所预测的y值就是这个值;
七、 正则化
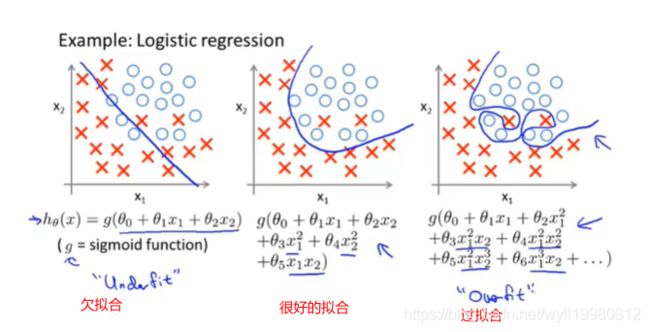
7.1 过拟合问题
过拟合:overfitting,模型有很多特征,使得假设模型可能会千方百计的去拟合训练集,努力地扭曲从而符合每个训练样本,虽然能让曲线的代价函数值很低,甚至为0,但这种情况会导致无法泛化到新的样本中,无法预测新样本的价格;
泛化:一个假设模型应用到新样本的能力,新样本数据就是训练集之外的数据;
- 1、减少特征变量:通过人工判断决定删除部分相干性低的变量,或者使用一些算法来剔除某些信息量少的特征;这个方法虽然能有效降低过拟合的发生,但可能会因为部分变量的剔除使得曲线拟合程度降低,或者我们并不想舍弃那部分信息;
- 2、正则化:能保留所有变量,通过减少量级来防治过拟合的发生,当特征很多的时候,每个特征都会对预测得y值或多或少的产生一点影响,我们不想舍掉它们,那么正则化就是最理想的方法;
7.2 代价函数

~~~~~~ 正则化的思想:在θ3和θ4前面加入惩罚项,即通过增大代价函数中θ3和θ4前面系数的大小来扩大两者对代价函数的影响,由于我们要使代价函数取最小,那么θ3和θ4必然取最小值(接近于0),那么,高次项的θTX就转化成了低次项的,从而简化模型,成功避免过拟合问题;

~~~~~~ 当特征很多时,我们无法确定哪个特征的相关性高,哪个相关性低,哪个是高次项,哪个是低次项,所以我们只能先将常数项之外所有的θ(θ1到θn)都作为正则项;
~~~~~~ 当然,如果我们λ设置得过大,那么会导致θ1到θn都被忽略,从而hθ(x)=θ0,它并没有贴合数据,如下图所示:

所以,正则化参数λ需要选择一个合适的值才能达到预期效果;
7.3 线性回归的正则化

Q:仅仅是θj变成了之前的0.99倍,这能够达到正则化的效果吗?

~~~~~~ 当样本个数小于特征个数时,该矩阵为奇异矩阵,无法计算逆矩阵,无法通过正规方程得到结果;不过,当λ>0时,整个矩阵的正则化就能解决以上问题,将其变成可逆矩阵;
7.4 logistic回归的正则化
梯度下降时防止过拟合,在后面加了和线性回归正则化一样的部分λ/m*θj;

进一步优化:

八、神经网络:表述
8.1 非线性假设
~~~~~~ 对于特征数很多的逻辑回归,其特征空间会膨胀,因为hθ(x)中会含有很多多次项,比如x12,x1x2,…;
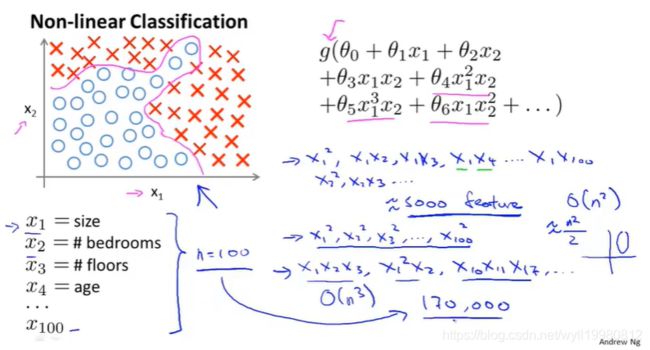
如果包含二次项的话,那么估计一共会有O(n2)项,考虑三次项则会有O(n3)项;
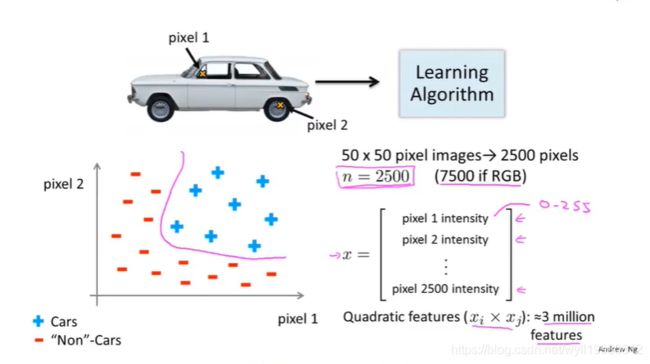
这是一种包含很多个特征的复杂的非线性假设问题;
Q:为什么提出神经网络?
~~~~~~ 只是包括平方项或者立方项特征,简单的logistic回归算法并不能在n很大时学习复杂的非线性假设,因此引入神经网络,它在学习复杂的非线性假设上被证明是一种好的多的算法,即使输入的特征有很多个;
8.2 神经元和大脑
~~~~~~ 大脑是个神奇的东西,把任何传感器移入大脑,大脑的自学习算法就能学会如何使用它,找出数据的方法,并学会处理它;
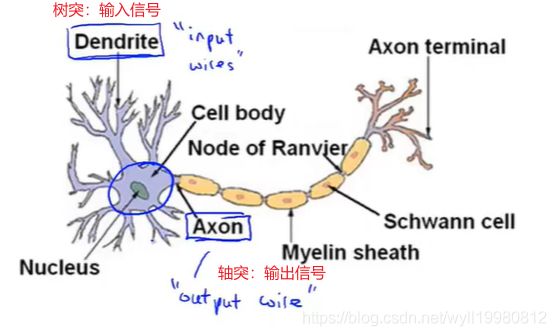
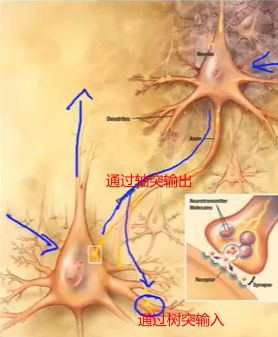
神经元模型:逻辑回归单元
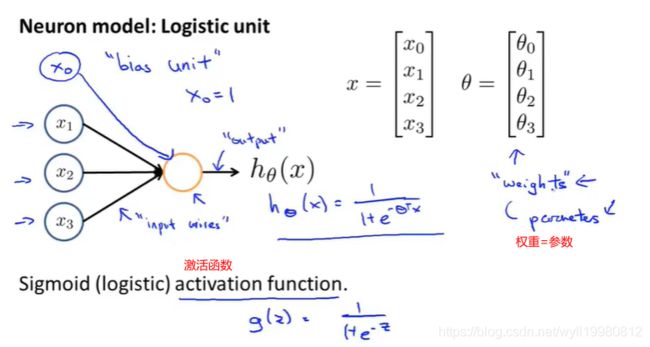
神经网络:多个神经元连接在一起的集合;
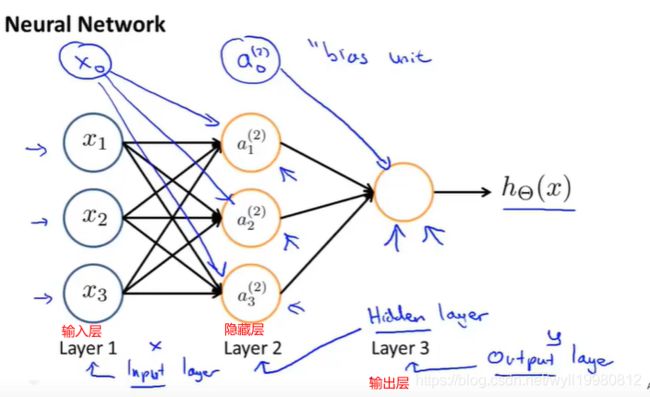

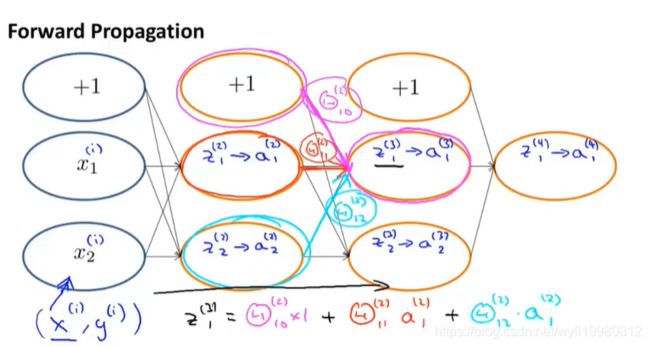
前向传播 Forward propagation
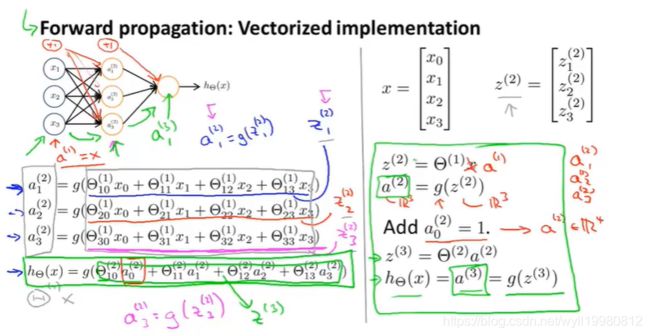

其它神经网络架构
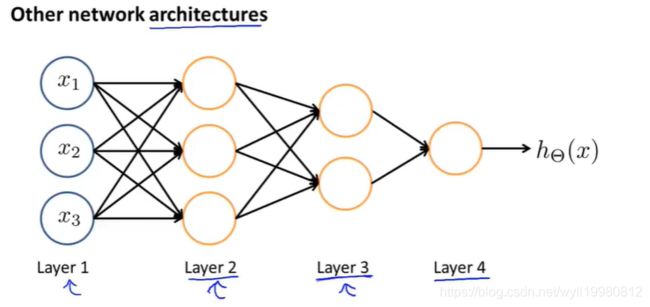
~~~~~~ 但都是后一层将前一层的输出当作输入进行处理,然后传给下一层;中间的隐藏层因为既有输入也有输出,所以它并不是单一的输入输出层;
上面都太抽象了,很懵;
8.3 神经网络举例
异或取反操作:

XOR表示异或操作;XNOR 和 NOT (x1XORx2)表示同或(异或取反),二者相同时才为真;

或操作:

至于权重(系数)怎么来的,这就是神经网络要解决的问题了,它通过调整权重来实现这些运算,好像是后面要学的反向传播;
取反操作:

用神经网络来将 三者转换成同或:
![]()
8.4 多元分类问题
一个输入,多个输出:

~~~~~~ 就是独热编码 one hot;
~~~~~~ 独热编码即 One-Hot 编码,又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。
例如:
自然状态码为:000,001,010,011,100,101
独热编码为:000001,000010,000100,001000,010000,100000
~~~~~~ 可以这样理解,对于每一个特征,如果它有m个可能值,那么经过独热编码后,就变成了m个二元特征(如成绩这个特征有好,中,差变成one-hot就是100, 010, 001)。并且,这些特征互斥,每次只有一个激活。因此,数据会变成稀疏的。
这样做的好处主要有:
- 解决了分类器不好处理属性数据的问题,将类别变量转换成新增的虚拟变量/指示变量;
- 在一定程度上也起到了扩充特征的作用;
缺点就是: - 特征量将会变得很多,数据经过独热编码可能会变得过于稀疏;
九、神经网络的学习
9.1 代价函数
9.2 反向传播算法
Back Propagation => BP神经网络

δ表示误差值,输出的aj(4)与yi的差值;
~~~~~~ 先计算结果,在根据误差调整参数,原理和逻辑回归差不多,只是过程复杂了,这个误差就是反向传播算法得到的,而结果则是前向传播算法得出;
前向输出,反向求参!

9.3 理解反向传播
9.4 梯度检验
~~~~~~ 使用神经网络进行类梯度下降算法时,最好附加使用梯度检验,能让算法优化一个级别以上,它能保证前向、反向传播百分之百正确;
曲线上某点的导数的近似值:双侧差分
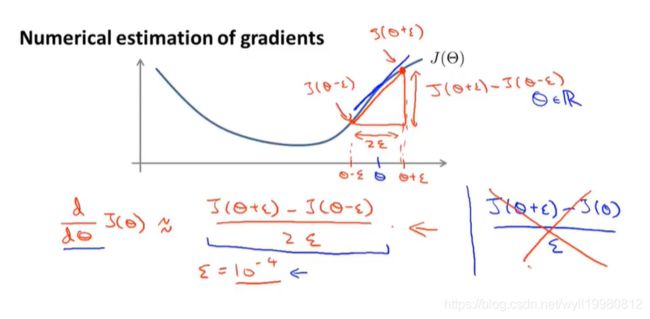
上面考虑θ是一个实数值的情况,下面则会进一步将θ看作向量:

for i = 1 :n,
thetaPlus = theta;
thetaPlus(i) = thetaPlus(i) + EPSILON;
thetaMinus = theta;
thetaMinus(i) = thetaMinus(i) - EPSILON ;
gradApprox(i) = (J(thetaPlus) - J( thetaMinus) )/(2*EPSILON);
end;
~~~~~~ 接下来检验这个 gradApprox ≈ DVec(反向传播得到的导数),从而验证反向传播是正确的;
整体步骤:
- 通过反向传播来计算DVec(D(1),D(2),D(3)的展开形式);
- 实现数值上的梯度检验,计算出gradApprox;
- 确保gradApprox和DVec是相似的值;
- 在训练样本/运行算法前,gradApprox检验程序务必要关闭,因为这个计算导数的程序需要很大的计算量,计算速度很慢,而反向传播中DVec的计算是高性能的;
如果在每次循环,或者每次梯度下降,都进行一次梯度检验,那么程序就会变得非常慢;
9.5 随机初始化
如何对θ初始化?
- 将所以参数初始化为0,在逻辑回归中是允许的,但在训练网络时基本起不到作用;因为在网络训练时,权重都初始化为0,意味着虽然每次都会梯度下降,但θ01(1)=θ02(1)的,这两个参数始终相等,且都不为零;
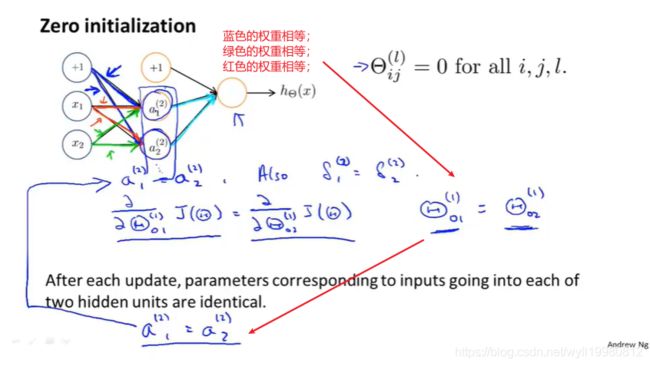
- 为了解决上面这个问题,神经网络中参数的初始化要具有随机化的思想,打破对称性;

9.6 总体回顾
- 第一步:选择神经网络架构;根据输入单元和输出单元个数选择合适的神经网络架构,一般隐藏层默认为1层(也是最常用的),如果选择大于1层,应保证每个隐藏层的单元个数相等;

- 第二步:训练神经网络;
- 随机初始化权重,权重很小,接近于0;
- 执行前向传播,即根据输入的x(1)得到hθ(x(i)),就是y值;
- 通过代码计算代价函数;
- 执行反向传播,算出偏导数项,也就是J(θ)关于参数θ的偏导数;
- 用for循环对每一个样本执行前向传播和反向传播,特别是第一次使用反向传播时,建议用for循环;

- 梯度检验,将这些偏导数值和数值方法得到的估计值进行比较;如果接近,则说明反向传播计算结果正确;
- 选择一个优化方法,也可以使用高级优化方法,内置到fminunc中,与反向传播相结合,从而最小化J(θ);对于神经网络,代价函数J(θ)为非凸函数,理论上可能停留在局部最小值;虽然不能确定是不是得到的全局最优值,但梯度下降法这样的优化方法通常表现不错,也能得到一个很小的局部最优值;

9.7 神经网络举例:无人驾驶

也需要驾驶员驾驶几分钟,让神经网络充足地学习了,在能够进行简单的自动驾驶,当前面都是路(传来的图片是一整块白色的时),神经网络学习的置信度明显下降,当又走到双车道,回到原来的那样子时,置信度又上升了;
十、应用机器学习的建议
10.1 决定下一步做什么
以房价预测为例,当预测时遇到很多无法接受的错误时,下一步该怎么做?
- 获得更多的训练样本;
- 减少特征数;
- 觉得目前的特征信息量不够,要获得更多的特征;
- 加入高次项系数(x12,x22,x1x2,etc)
- 减小λ;
- 增大λ;
~~~~~~ 这些选择中任何一个都可能需要大几个月的时间才能完成,而最糟糕的是完成之后你觉得效果还是不怎么理想;
通过下面几节来学会评价模型并做出正确的改进选择来达到目的;
10.2 评估假设
如何判断我的假设是不是过拟合?
-
将样本数据分成两部分:训练集和测试集,典型的方法是按照7:3的比例,如果数据的分布有规律或者某种顺序,那么最好随机选择7:3;
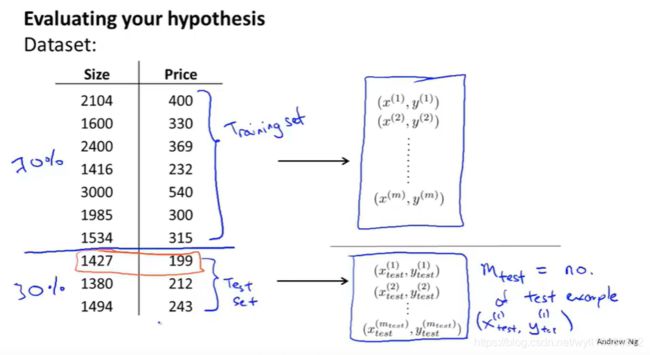
-
训练那70%的训练数据,得到参数θ和训练误差J(θ);
-
计算测试集误差Jtest(θ),这个θ是上一步训练训练集数据得到的参数θ;即后面30%测试数据的代价函数值;

逻辑回归和线性回归的步骤差不多,涉及到一个错误分类误差以及不同的代价函数;

10.3 模型选择和交叉验证集
确定多项式参数;
过拟合->泛化能力差;
选择正确且合适的特征;
评估假设:
6:2:2 => 训练集:交叉验证:测试集;

从而可以计算出它们对应的误差;

都是一个公式;

~~~~~~ 意思就是用训练集来训练θ,用交叉验证集来选择多项式(选择验证误差最小的模型),用测试集来判断它的泛化能力;
在原来的基础上更加严谨;
10.4 诊断偏差与方差
随着多项式次数增大,训练误差会越来越低,拟合得越来越好;而验证误差会先减少后增加;

导致验证误差大的两个问题:两个高偏差,高方差;
通过训练误差和验证误差共同确定是高偏差问题还是高方差问题;
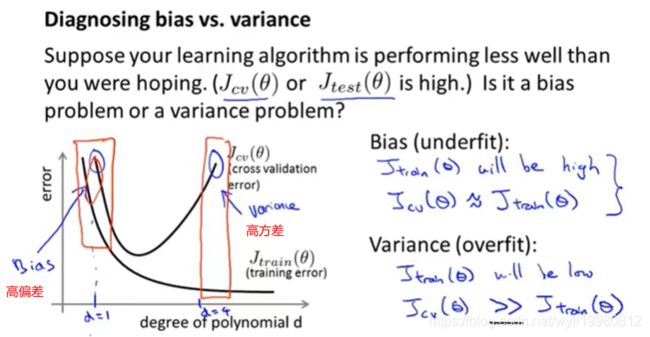
高偏差:训练误差和验证误差都很大;
高偏差:训练误差小,验证误差大;
10.5 正则化和偏差、方差

选择一个合适的λ值,从而最小化代价函数,得到合适的θ值;
Q:如何选择出一个合适的λ值?

说白了就是一个个λ试,因为λ在代价函数中,每确定一次λ值就对代价函数进行最小化,得到对应的θ => λ和θ是关联的;确定若干组θ后,代入验证误差方程中取误差最小的那组θ;若其对应的λ很小,则可以忽略,代价函数直接用不加正则化,否则,不能忽略正则化;

λ越大,正则化级别越小,高次项前面的参数的重要程度越高,训练误差越大,越倾向于欠拟合;
λ越小,正则化级别越高,高次项前面的参数的重要程度越低,训练误差越小,越倾向于过拟合;
10.6 学习曲线
~~~~~~ 使用学习曲线检查你的学习算法是否运行正常,以及是出现高偏差问题还是高方差问题,改进你的算法;
~~~~~~ 训练样本数很小时,训练误差也会很小,因为很容易就把训练集拟合到很好;而随着训练样本数的增加,训练集的拟合程度可能开始下降,训练误差可能变大;
~~~~~~ 而交叉验证集误差和测试集误差却相反,它们会随着训练样本数量的增加而减小,因为训练样本少的时候,虽然拟合得很好,但数据的泛化程度小,无法对训练集以外的数据进行很好的预测,从而导致验证误差、测试误差大;

对于高偏差情况:
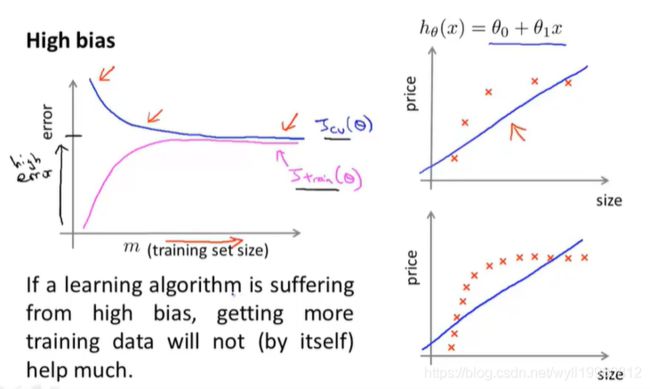
~~~~~~ 当m很小的时候(可以想成m=1),那么训练集的高偏差无疑会很小,因为它会完美拟合这个样本,而代表泛化能力的交叉验证集的高偏大就会很大,因为泛化能力差;
=> 即对于高偏差的情况,随着样本数量持续增加,验证集的偏差基本保持不变,所以此时增加样本数量对改善算法无意;
对于高方差情况:

~~~~~~ 训练集误差随着样本数量增大而增加,但误差终究还是很小,因为样本越多越难拟合;而为什么验证误差和测试误差会随着样本数量增大而降低???我认为应该是当样本数量增加到一定程度时,原次项方程无法对它做出误差很小的拟合,这将使得过拟合程度下降,使交叉验证误差降低;
~~~~~~ 所以,对于高方差情况,增大训练样本数对算法的优化有一定的帮助;
~~~~~~ 所以,很有必要知道自己的算法是高偏差(欠拟合)还是高方差(过拟合),因为它可能会告诉你是否有必要花时间来增加更多的训练集数据;
10.7 决定下一步做什么
回到一开始的问题:
以房价预测为例,当预测时遇到很多无法接受的错误时,下一步该怎么做?
- 获得更多的训练样本;对高方差有用;
- 减少特征数;对高方差有用;
- 觉得目前的特征信息量不够,要获得更多的特征;解决高偏差问题;
- 加入高次项系数(x12,x22,x1x2,etc);适用于高偏差问题;
- 减小λ;适用于高偏差问题;
- 增大λ;适用于高方差问题;

十一、机器学习系统的设计
11.1 首先要做什么

~~~~~~ 比如:对于一个垃圾邮件分类系统,我如何做才能对垃圾邮件进行分类?
~~~~~~ 监督学习:建立1个单词组,里面存放垃圾邮件中经常出现的单词,比如:deal、buy、discount…,这里单词的个数就是特征数,x=[0,1,1,0,…]T代表对应单词是否出现,根据这个作为样本进行输入,y=1/0表示是否为垃圾邮件;往往在实际中会将单词组中单词的个数增加至上万;
Q:如何让你设计的这个分类器误差更小呢?

一般而言,会随机地使用这些方法;
11.2 误差分析
- 先快速设计出一个简单粗暴的算法,尽管效果可能不是那么好,训练、交叉验证和测试它;
- 画出学习曲线,看是增加数据还是增加特征;
- 误差分析:看那些被错误分类地样本,具有什么样的特征,它们之间有什么共同点,从而决定是否对算法现有特征进行修改;

通过那些分类错误的样本,很容易找出算法的不足所在,然后集中精力处理它们;

单一规则的数值评价指标,比如:交叉验证错误率,来评估算法;
在优化过程中,以这个指标为依据判断此次优化是否有效;
不要花大量时间在第一步上构造,在错误样本中找解决方案往往更高效;别担心算法太简单or不高效,先用算法弄出结果,再误差分析,根据评价指标以及误差分析来优化算法,从而确定该添加什么,该放弃什么;
11.3 不对称性分类得误差评估
考虑一种情况——偏斜类情况:
错误率 > 样本中某类样本的占比,比如错误率1% > 癌症检测样本中得癌症的人占比0.5%;
这样即使我把全部数据预测为不得癌症(y=0),我也只有0.5%的错误率,看起来算法表现得很好;
=> 获得更低的错误率 有时候并不代表 分类模型的质量得到提高,比如偏斜类情况;

解决偏斜类问题:

查准率 precision:即准确率,对于我们预测的所有患癌症的病人中,他们有多大概率真正患有癌症;precision=真阳性/预测阳性;(预测阳性=真阳性+假阳性)
召回率 recall:如果所有的病人确实得了癌症,有多大比率我们正确预测到他们得了癌症;recall=真阳性/实际阳性;(实际阳性=真阳性+假阴性);
~~~~~~ 两个值越高越好,比如我预测所有y都为0,显然召回率为0,因为真阳性为0 ,一下就能看出来这是偏斜类情况;但是此时,查准率为无穷大,我们需要权衡二者来得到我们想要的信息;
11.4 查准率和召回率的权衡
Q:如何自动选取阈值?才能更好地权衡二者
通常不知道哪种好,所以需要一个评估度量值;
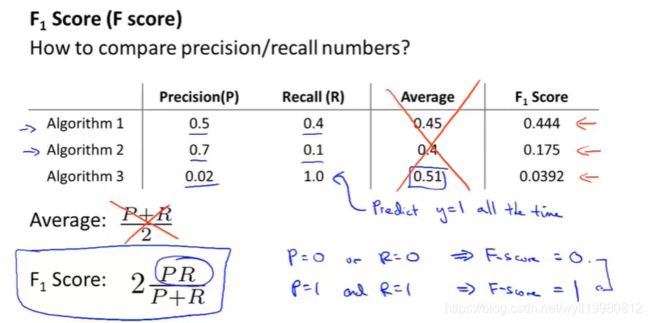
F1值(调和平均):F1=2PR/(P+R),二者中任意一个不为0,F值能很好的结合以上特点进行权衡;
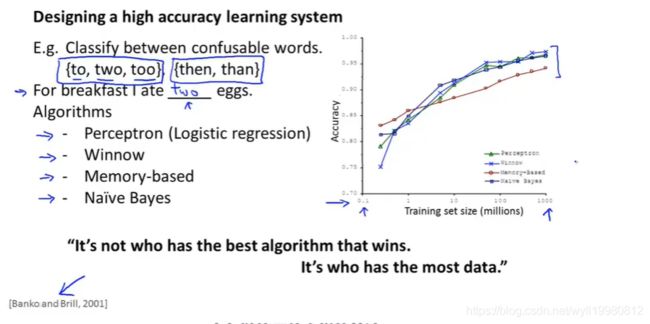
11.5 机器学习数据
~~~~~~ 不同的算法随着样本数量的增加,其精确度的变化幅度也会不一样,有的算法可能一开始精确度低,等样本数量上来后,精确度提高很大幅度;
大量数据只在一些情况下有作用;


~~~~~~ 如果你有大量的数据,你设计了一种带有很多参数的学习算法,那么这将会是一个很好的方式来提供一个高性能的学习算法;(数据量远大于参数的话,过拟合的可能性不大);
十二、支持向量机
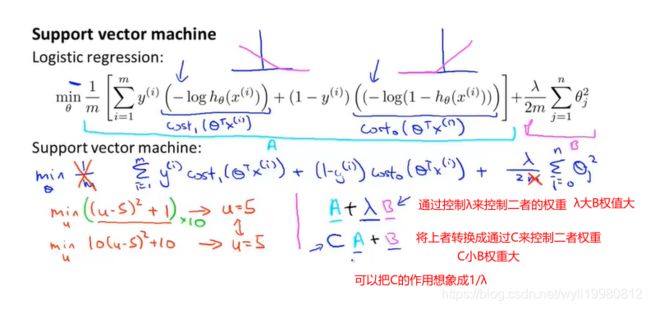
12.1 优化目标
SVM:support vector machine;


把代价函数分成两部分,比如左边:hθ(X)=1/(1+e-z),当z趋向于很大的数时,hθ(X)才能取到1;
支持向量机:
12.2 大边界的直观理解
支持向量机=大间距分类器?
什么是向量机,我们如何理解它,有什么作用?

假设C非常大,那么我们优化代价函数只需将A部分尽力优化成0即可,那么可做出如下假设:
假设A被优化成0:

比如:
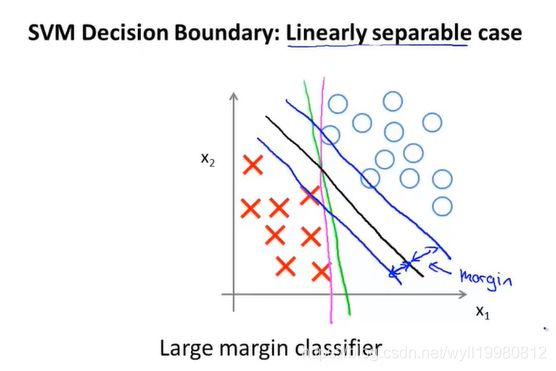
~~~~~~ 未使用支持向量机时,决策边界可能是紫色的或者绿色的那条,可以看出它们非常贴近数据集;
~~~~~~ 而使用支持向量机画出的决策边界的间距(黑色线),很明显拥有更大的间距,能够更好的夹在两个数据集中间;
~~~~~~ 更大间距->更好的鲁棒性;
 ~~~~~~ 当C非常大的时候,决策边界会对某个异常点敏感,比如没有左下角的红×时,决策边界是黑线,当加上那么一个异常点时,决策边界可能立马变为紫色的线;而这都是基于C很大的情况;
~~~~~~ 当C非常大的时候,决策边界会对某个异常点敏感,比如没有左下角的红×时,决策边界是黑线,当加上那么一个异常点时,决策边界可能立马变为紫色的线;而这都是基于C很大的情况;
如果C很小,那么决策边界并不会对某个或者一些异常点敏感,比如上面正集混入一些负集等等,它还是能划出一条合理的分类边界;
所以C的取值问题才是SVM的核心,C取得不那么大时,才能既有大边界又能对某个/些异常数据不敏感;
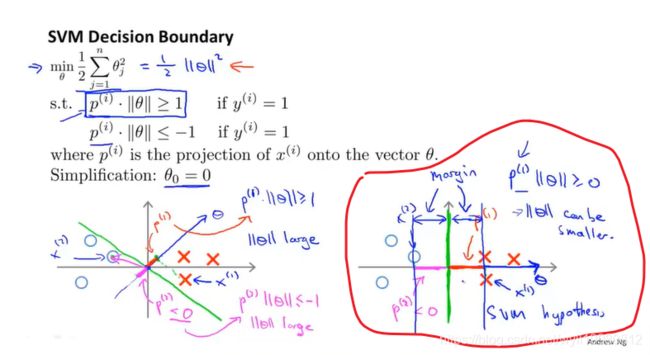
12.3 数学背后的大边界分类
为什么这么优化呢?如何得到大间距分类器的?
更好地理解SVM;
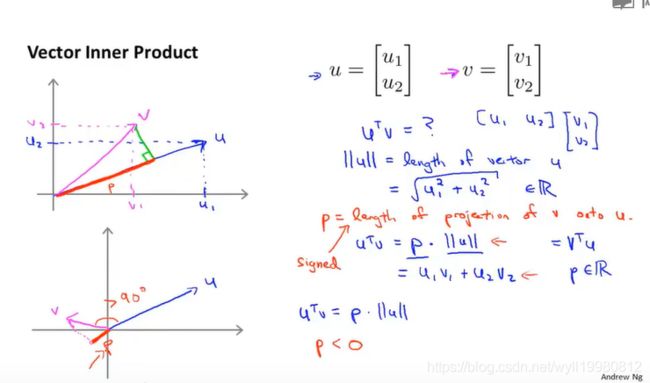
欧几里得长度;
vTu内积=v在u上的投影长度*u的长度;
p是有符号的;

当C取很大得值时,A部分就要最小化为0,此时代价函数=1/2||θ||2;

~~~~~~ z=0时,假如边界函数如绿色线所示,θ与决策边界垂直,那么对于x(1)和x(2),它们在θ上的投影长度都很小,那么为了满足条件p(i)·||θ|| ≥1或者p(i)·||θ||≤-1,则||θ||就要取很大的值,这与之前最小化代价函数(1/2||θ||2)相矛盾;
支持向量机试图让p(i)(训练样本到决策边界的距离)变得足够大,从而让θ的范数变小,最小化代价函数;
这就是SVM如何产生大间距分类现象的;
12.4 (高斯)核函数1
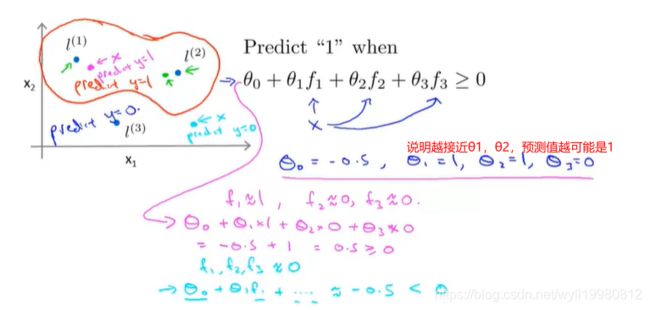
非线性决策边界
本节问题:
- 什么是高斯核函数?
- 运行机理

f(i)表示相似度;
相似度的度量=>相似函数=>核函数=>高斯核函数=>k(x,l(i));

给定一标记点 l1,如果样本x距离 l1 近,那么这个f1的值接近于1,隔得越远,越接近0;
12.5 (高斯)核函数2
本节问题:
- 如何求解这个相似方程?
- 标记点如何设置?
使用SVM+Kernels

有m个样本就选m个标记点;将计算出的m个相似度合成相似度向量 ( +f0 就是m+1维);


低偏差、高方差就是图像有较大的斜率,不那么平滑;
高偏差、低方差就是图像较平滑;
高斯分布=>正态分布;
12.6 使用支持向量机
本节问题:
- 如何使用SVM软件进行求解;
- 如何选择一个合适的核函数;
支持向量机并不能很好的应用在逻辑回归;
C的选择、核函数的选择;

计算核函数的向量值;

进行特征缩放,放置特征中量级较大的特征过度影响||v||2;

核函数应该要满足的条件(并不是所有的函数都能作为核函数):
Mercer定理;
其它核函数:
- 多项式核函数;一般表现较差 ,用的不多;
- 卡方核函数;
- 字符串核函数
- …
多分类问题:


SVM是一种凸优化,不用担心局部最优;
SVM比神经网络快,它是一种体系,一个有效的方法去学习复杂的非线性函数;
十三、聚类
13.1 无监督学习
13.2 K-Means算法
聚类算法——K-Means算法;
本节问题:
- K-Means算法的原理;
- K-Means算法的使用;
随机初始化N个聚类中心;
while(true)
{
簇分配:计算所有点到这N个聚类中心的距离,从而把数据分为N个簇(隔得最近的一个簇);
计算均值:对于每一个簇,计算各点到该簇聚类中心的距离,取平均值
移动聚类中心:移动该聚类中心到平均值处;
}

距离是欧几里得距离;
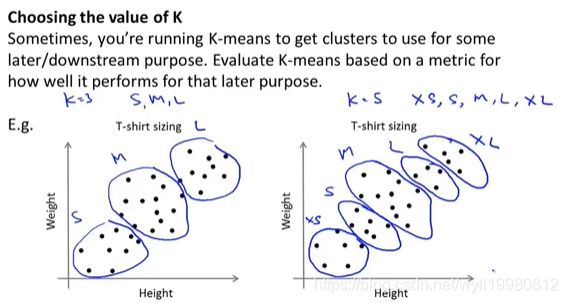
![]()

衣服尺寸的划分有点像是无监督算法的市场化;
Q:如果有一个聚类中心,它没有被分配到任何一个点,怎么办?
A:一般情况移除这个聚类中心,但是聚类中心就会从K变为K-1;如果想保持K个聚类,则在初始化这个点一次;
13.3 优化目标
本节目标:
- K-Means算法的优化目标是什么,为何这么定义?
失真函数

两步最小化,给聚类中心分配点时以及移动聚类中心时;‘
13.4 随机初始化
本节问题:
- 如何随机初始化?
随机化初始聚类中心,其实就是在样本中随机选k个点作为聚类中心;
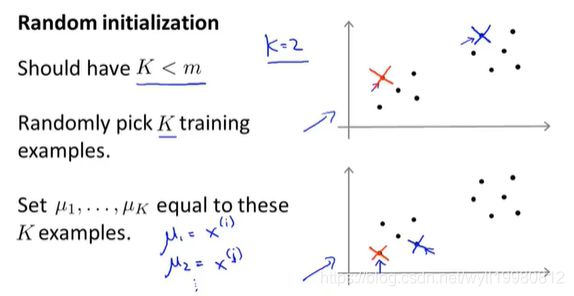
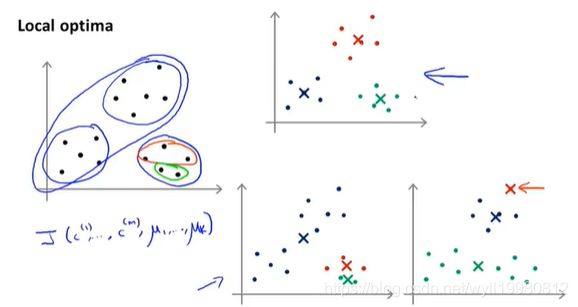
K-Means算法可能落在局部最优;
解决局部最优问题就是多次随机初始化,找到最好的解(畸变函数最小,即代价最小);
 如果聚类数很少,比如3,4,5个,那么多次随机初始化会有明显的较好的结果,如果聚类数很多,那么下一次随机初始化不一定比上次有多大的进步;
如果聚类数很少,比如3,4,5个,那么多次随机初始化会有明显的较好的结果,如果聚类数很多,那么下一次随机初始化不一定比上次有多大的进步;
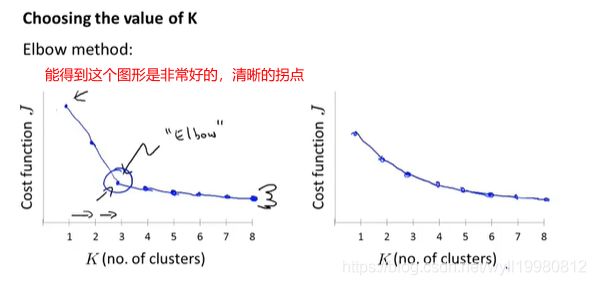
13.5 选择聚类数
本节问题:
- 如何选择合适的聚类数;
常用方法还是观察可视化图,手动选择;因为数据的无标签特性,也是无监督算法的特性,所以自动选择聚类数量是很困难的;
肘部法则:前期随着K增加 J明显下降,后期缓和下降,那么拐点处一般作为K;但如果这个图像不怎么明显,而是缓和下降,那么这个法则就难以适用;
十四、降维
14.1 应用一:数据压缩
本节问题:
14.2 应用二:数据可视化
本节问题:
- 降维是如何对数据可视化起到作用的?
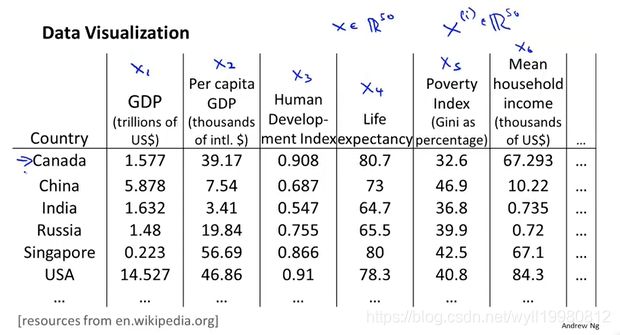
~~~~~~ 用一个不同的特征来表示它,加入这里有50个特征,我们用两个不同的特征来表示它们,相当于对于每个样本,我用2个数组表示50个数字;


对于降维在数据可视化中的应用,通常k选择2,3,从而方便画图展示;
14.3 主成分分析PCA
本节问题:
- 了解降维的一种核心方法——PCA;
- PCA的原理;
- PCA同线性回归的区别;
- 主成分分析的步骤;
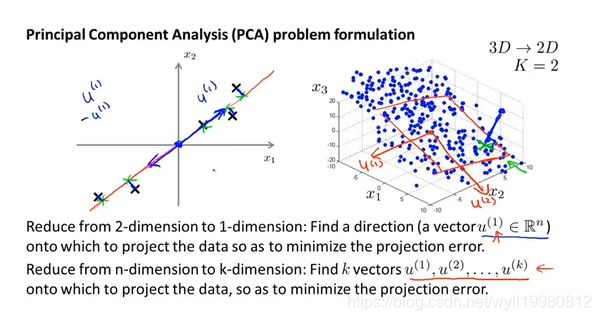
~~~~~~ 试图找一个投影(可以是平面可以是线)来把数据投影到上面,使投影误差(点到直线的距离)最小;
主成分分析降维的同时,也带来一定的误差,即与原始数据相比,数据可靠性降低;看取舍 ;
假设常数项为0,直线过原点更容易观察;

~~~~~~ 向量;一个或者多个向量构成直线或者多维空间;找出若干向量,将数据投影到这k个向量展开的线性子空间上;k维平面,若是2维平面,距离就是原3维空间上的点到二维平面的距离;
PCA和线性回归的区别:
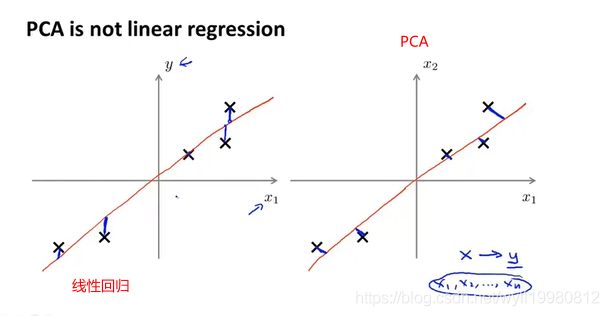
线性回归最小化的是实际y值到预测y值的平方差,而PCA最小化的是点到直线的距离的平方;
线性回归用一个x值来预测y值;
PCA将所有x值转换为别的值;


1、在进行PCA之前,先均值归一化和特征规范化;
2、数据预处理
3、特征缩放
4、主成分分析
协方差
正定矩阵
奇异值分解

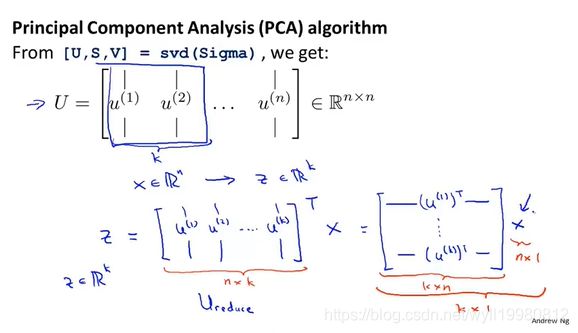
7、用到的就是那个 U 矩阵,用于线性变换,得到向量z,z是k维向量,其实就是整个投影过程的变换;

14.4 重建的压缩表示
本节问题:
- 如何把降维后的数据恢复到以前维度;
原始数据的重构问题:

其实就是一个矩阵求逆的过程,不过求出来的Xapprox和以前的X会有一定的误差,因为存在投影误差;
而对于U矩阵,它是正交矩阵,转置等于逆,所以这里直接Xapprox=UreduceZ;
14.5 选择主成分的数量
本节问题:
14.6 主成分分析的应用建议
本节问题:
- PCA如何加快学习算法的执行效率;

在监督学习中对高维的样本使用主成分分析降维,比如10000维数据降到1000维,几乎不影响精确度,PCA后回归能够大幅度提高效率;

~~~~~~ **错误应用之一:使用PCA防止过拟合;**它可能效果会很好,但这不是解决过拟合的方式,因为它实际特征并没有减少(比如99%的方差被保留),还不如使用正则化;

建议:
- 不要一开始就使用PCA,最好先使用原始数据,只有当原始数据进行不下去了才考虑PCA;
- 与其考虑降低维度,不如想想如何优化算法;
十五、异常检测
15.1 问题的动机
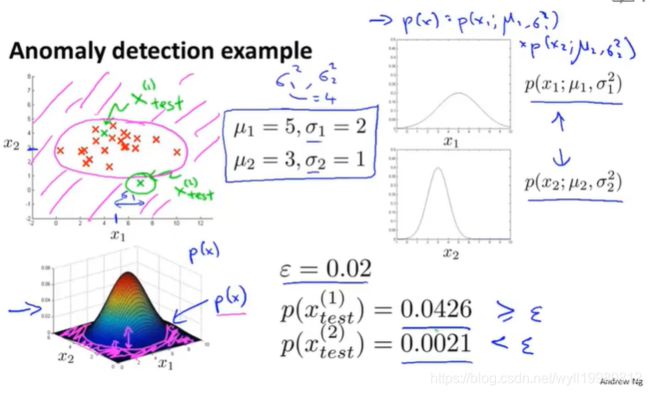
飞机引擎检测:给定一系列正常的引擎参数,要求确定一个新生产的引擎是否正常;
异常用户检测:网站检测用户刷新频率,登录次数、登陆位置等信息,判断用户行为是否异常;
数据中心的计算机检测:检测计算机内存消耗、硬盘容量等信息,判断计算机是否异常;
15.2 高斯分布
本节问题:
高斯函数分布图象:
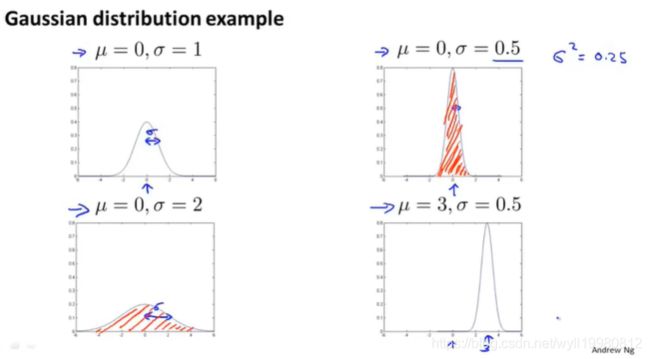
概率密度函数与x轴的面积为1,即积分值=1;
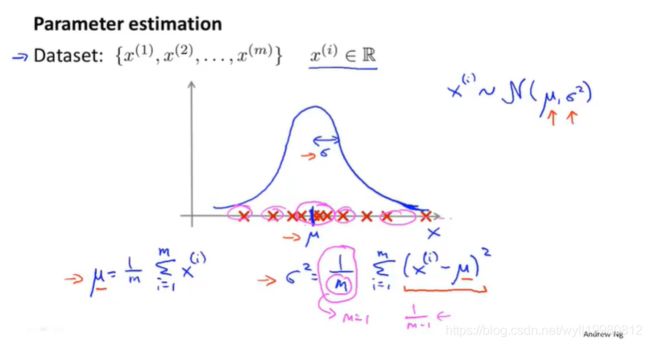
15.3 算法
本节问题:
- 如何用高斯分布推导异常检测算法;
密度估计

每个特征有每个特征的高斯分布,独立同分布;即使每个特征不独立,这个算法也能进行;
15.4 开发和评价一个异常检测系统
本节问题:
- 开发一个异常检测系统用于实际问题;
- 如何评估一个异常检测算法;
加入带标签的样本后,这个不就相当于监督学习了吗?
训练+预测;

step1:用无标签样本训练(假设样本都是无异常的),拟合p(x);
step2:输入交叉验证集(含异常和正常样本),预测y的值;
step3:算法成功预测的次数对算法进行评估;但这里不能直接用分类正确率,因为前面说过,倾斜的数据集(大部分y=0,小部分y=1)不适合用它作为评价指标;还是使用精度,召回率它们;
step4:确定阈值€:使用不同的阈值,最终采用能最大化F1-score的阈值€;
step5:确定模型和参数后,就可以用测试集来评估这个模型系统;
15.5 异常检测 VS 监督学习
本节问题:
- 异常检测与监督学习的区别;
- 异常检测往往是有大量正样本和少量负样本或者大量负样本和少量正样本,伴随着倾斜的情况;而监督学习则是拥有大量的正样本和负样本;
- 有时候需要知道是什么原因(特征)导致样本异常,此时在监督学习中很难做到,而选择大量负样本、少量正样本的异常检测中就方便多了;如果仅仅是判断新样本是否为正负样本时,监督学习拥有海量样本信息,能够做出很好的判断;
15.6 选择特征
本节问题:
- 如何选择适当的特征来实现异常检测;
- 误差分析
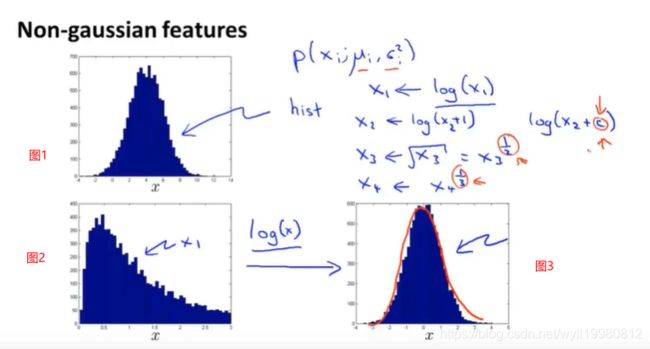
~~~~~~ 画出某个特征的数据分布图,例如画出来如图1所示,那么它的分布自然就很像高斯分布,可以考虑作为特征来实现异常检测;
如果画出来如图2,那么很明显不像,需要做出一点变换,比如log(x)来让它更像高斯分布;log适合处理拖尾的;不同的图像,处理的函数也不同;
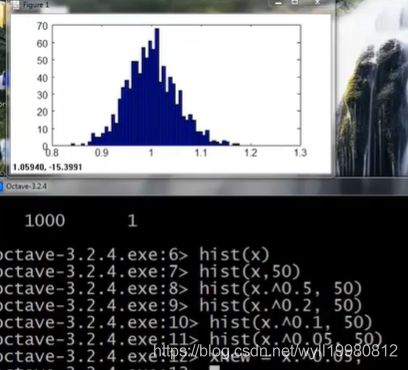
误差分析步骤:
~~~~~~ 同监督学习,先简单地搞出一套完整的算法,然后用验证集对其进行验证,然后对判断错误的验证集样本进行分析,看能不能找到一些其他的特征,让这些判断出错的样本能表现得更好;

灵活的建立新的特征or选取特征,比如计算机指标监控:

~~~~~~ 如果服务器卡在某个死循环,那么CPU负荷增加,但网络流量并不会变,就可以新建一个特征x5=CPU Load / network traffic,当这个值突然骤升,说明肯定出现了这个问题;
这里比较适用于时序数据的监控;
15.7 多元高斯分布
本节问题:
- 多元高斯分布的作用;
- 如何理解多元高斯分布,作用原理;
多元高斯分布看起来适用于这样的场景:
~~~~~~ 对于x1,x2两个特征,有一定的联系,但某样本在x1,x2的取值在各自的高斯分布上都不算太差,那么异常检测算法会将其划分为非异常点,而实际意义上它很可能是异常点,需要同时考虑x1,x2两个特征值;



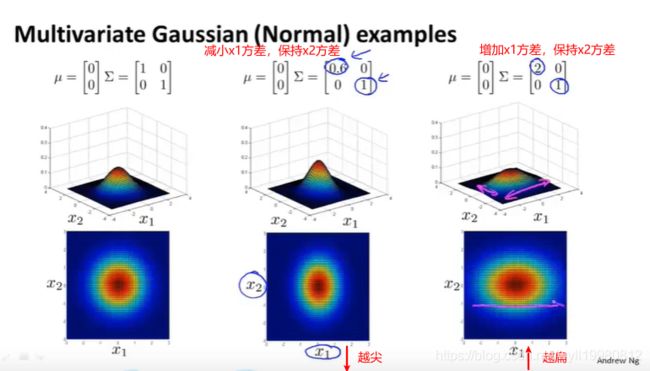
用数据的相关性建模:


改变μ就是改变中心点的位置;
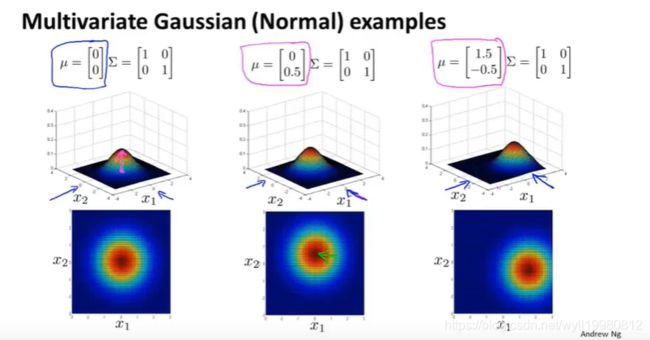
能不能新建一个特征x3=x1/x2呢?
这是可以的,创建新的特征来捕捉异常的组合值;而多元高斯模型只是自动化了这个操作;
15.8 使用多元高斯分布进行异常检测

相当于增加了特征值之间的相关性;
![]()

这两个限制条件:m>n & 非冗余 保证了Σ可逆,从而才能继续下去,遇到这两个文件的概率非常低,基本不用担心;
十六、推荐系统
最重要的机器学习应用领域之一 ——推荐系统;
推荐系统其实即使自动的特征学习;
16.1 问题形式化
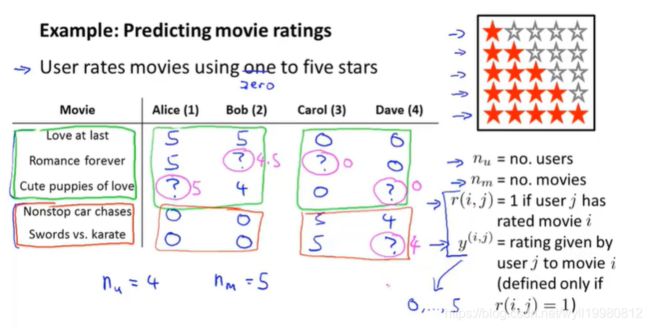
给出 r(i,j) 和 y(i,j) 预测上图中的?,预测用户喜欢的类型,并将其没看过的属于喜欢的类型的电影推荐过去;
16.2 基于内容的推荐系统
假设:假设我们得到了电影的特征;

这个θ(1)是假设出来的,实际上要通过训练得到;
参数θ的训练:跟线性回归有点像


优化目标函数和梯度下降更新:

最终得到不同用户对不同电影的评级;
16.3 协同过滤
本节问题:
- 了解协同过滤算法的基本原理;
- 对比于基于内容的推荐算法,有何改进之处;
协同过滤的特性之一:特征学习,feature learning;
它不用基于上面方法的假设;
假设我们先得到θ,即用户喜欢某类电影的程度,;
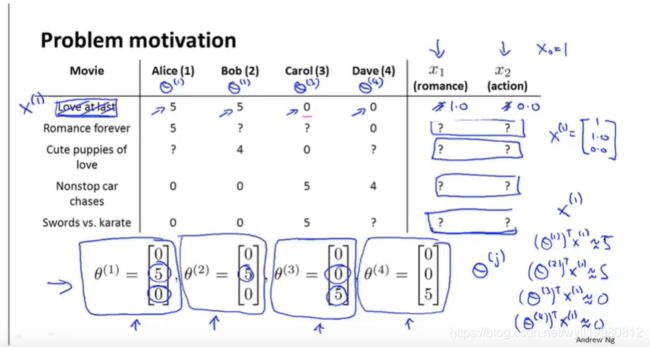

基于内容的推荐算法 vs 协同过滤:
- 前者通过 电影特征+用户对电影的评分 = > 训练出用户对不同类电影的喜好程度 + 推测出用户对其它电影的评分;
- 后者可以不给出θ,同样可以学习出特征值,然后根据特征值改进θ:
- step1:随机初始化θ,通过协同过滤学习并预测电影特征值;
- step2:通过电影特征值学习并预测更好的θ
- 回到step1,往复循环。。。。。。
- 最终算法收敛到合适的电影特征值和θ;
- 用户对电影的评分 = > 训练出电影的特征 + 用户对各类型电影的喜好程度 +推测出用户对其它电影的评分;

- 即用参与评价的用户来帮助特征学习;
16.4 协同过滤算法
协同过滤的这一算法能直接将θ和电影特征解出来,避免往复迭代:
即把两个优化目标函数结合;

不包括θ0和X0这里学习的都是n维;
16.5 向量化实现
解决这个问题:用户A一直在找商品B,你能不能想办法推荐给A一些类似于B的商品;
低秩矩阵分解:

XθT为低秩;
由于电影特征个数的不确定,如何保证XθT后的矩阵维数???
在这里,电影分多少类,说明每一步电影就有多少特征值,保证θ(i)和x(j)的维数一致应该就行了;

两部电影的特征向量之间的距离越小,越相似;
16.6 均值归一化
本节问题:
十七、大规模机器学习
17.1 大型数据集的学习
大型数据集的学习带来的是计算问题;
本章学习如何处理上亿级别的大型数据集;

17.2 随机梯度下降法
本节问题:
- 随机梯度对比于普通梯度下降法,改进在哪?
批量梯度下降:

~~~~~~ 默认的是(批量)梯度下降法,Batch Gradient Descent:即每次都要考虑一批(所有)的训练样本这才完成迭代的一步,所以,它的计算复杂度太高;
随机梯度下降:
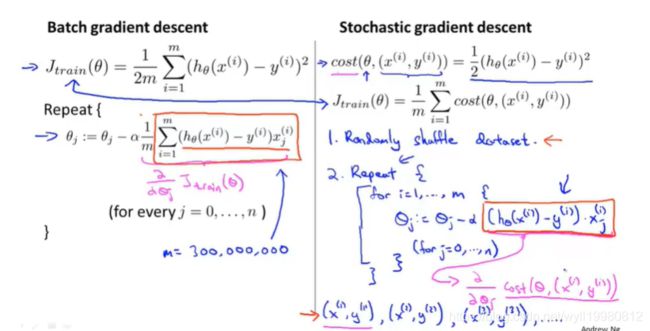
代价函数为当前样本上的表现;
对每个样本都遍历,遍历时调整θ使图像在该样本处拟合得好一点,cost代价低一点;
每次只关注一个训练样本 ;遍历过程中,虽然很曲折,但也是朝着全局最优前进(偶尔会有例外,因为是随机的 ),它可能在最小值周围徘徊;

也可能不止一次遍历所有样本,但次数不会超过10次;
17.3 随机梯度下降收敛
本节问题:


随着算法进行,迭代次数(遍历的样本数增加),iterationNumber增加,α越来越小;
小的α能让算法更接近最小值;
17.4 小批量梯度下降
Mini-batch,小型的梯度下降;
假设一次处理的小批量为10个样本:

夹在批量梯度下降和随机梯度下降中间,下降路线曲折度没有随机梯度的曲折,计算速度也比批量梯度的快(有时候比随机梯度下降还要好);

缺点就是:要根据小批量样本数的个数B,来确定组数;
17.5 在线学习
从用户身上的数据流上学习;

如果你有源源不断地数据(大量用户涌入网站),那么你就不需要多次使用一个数据了,也没必要标号了,用完就丢;
对不同的用户群体分配不同的方案,杀熟;

比如我有100台手机,当用户搜索1080P时,我要选择性的根据用户群体的不同,列出10台最适合该用户的手机,以最大化可能性促使他购买;;以10步梯度下降法来更新参数;
17.6 映射化简和数据并行
本节问题:
- 了解MapReduce的原理;
- 为什么MapReduce过时了;
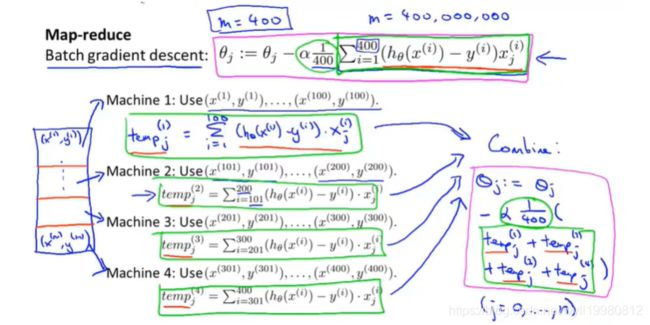
比如400个样本的批量梯度下降法,分割成4组,每组100样本,由四台机器并行完成,然后汇总到中心服务器,速度提升四倍(由于网络通信等外部因素,不会刚好提升四倍);
把MapReduce看成一台机器的多核并行,而不是多台机器并行,这样就不用担心网络延迟了,通信传输也需要时间;
mapreduce为什么被淘汰了?
十八、应用实例:图片文字识别OCR
18.1 问题描述和流程图
18.2 滑动窗口
本节问题:
- 如何在图片中检测到文字?
人像识别:
矩形框;

正负样本,分类,监督学习;

1、选中图片左上角矩形框;
2、传入分类器,检测y0 or y1,返回;
3、矩形框右移(事先设定的步长),重复判断;
4、移到最右边后下移,重复;
5、移到末尾后,第二遍,增大窗口,重复;
OCR识别:

正负样本训练;

一小块一小块的检测;
放大算子:把白色区域扩大;
忽略奇怪的矩形(比如瘦高的,交叉的);

字符切割;训练分类器;

OCR流水线文字识别:

18.3 获取大量数据和人工数据
本节问题:
- 如何获得大量数据?
人工合成数据的两种方式:
- 从零生成;
- 已有小部分训练集,通过某种方式扩展;

灰度图像;
利用字体库;
将字母换个字体形式然后贴到别的背景中;
这基本从零开始生产;
第二种方法:一个样本扩展成多个样本


失真合成数据,保证失真是合理的;


首先要确保分类器偏差较低,才大量合成人工数据;
最好画个学习曲线,便于观察分析;
18.4 上限分析:下一步工作
在设计完一个机器学习系统后,我们需要对整体以及各个模块进行分析;
比如这里的OCR文本识别:

~~~~~~ 刚刚设计出系统,72%的准确率,我们开始采用控制变量法对各个模块逐个分析;
~~~~~~ 首先文本检测模块,对每个文本区域都设立正确的文本检测结果(仿真出100%正确检测图片中的文本信息),此时第一个模块正确率将达到100%,这时候我们再测试整体的正确率,为89%;
以同样的方式处理第二个模块:
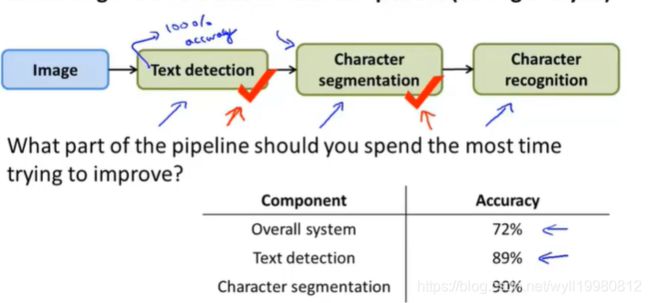
准确率提高到90%;
继续处理第三个模块:
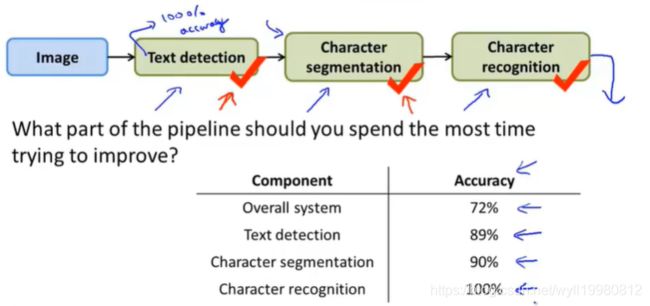
这样我们就能知道各个模块的提升空间有多大,针对性地改善;
这里明显第一个模块:文本检测模块最有潜力改善,所以我们应花费更多的精力在第1、3两个模块;
例如这个人脸识别:

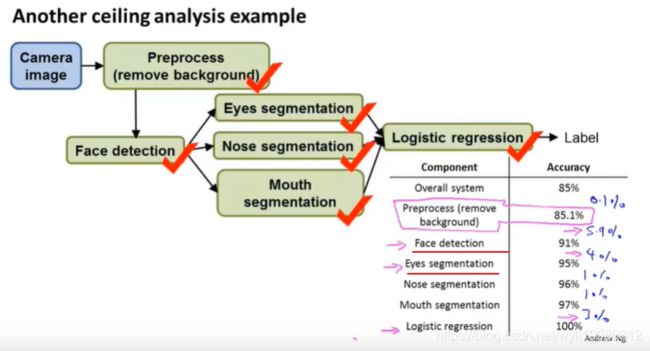
不要花费大量时间去做一些没有意义的事情;
把时间都用在最有价值的事情上;
上限分析的必要性;