机器学习之支持向量机
一、支持向量机的概念
支持向量机(Support Vector Machine)是一类按监督学习方式对数据进行二元分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane)。
SVM有三宝:间隔、对偶、核技巧
SVM有三种:hard-margin SVM、soft-margin、kernel SVM
给定训练样本集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) , } , y i ∈ { − 1 , + 1 } D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m),\},y_i\in\{-1,+1\} D={ (x1,y1),(x2,y2),...,(xm,ym),},yi∈{ −1,+1},在样本空间中找到一个超平面,尽可能将不同类别的样本分开,使得这个划分超平面所产生的分类结果是最鲁棒的,如下图中的粗线部分。
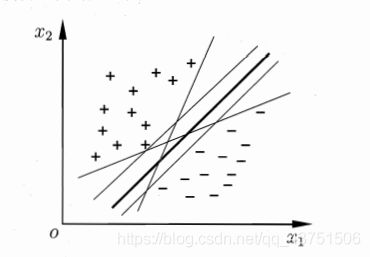
划分超平面可通过如下线性方程来描述:
w T x + b = 0 w^Tx+b=0 wTx+b=0
其中 w = ( w 1 ; w 2 ; . . . w d ) w=(w_1;w_2;...w_d) w=(w1;w2;...wd)为法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离,划分超平面被法向量w和位移b确定。
支持向量机 f ( x ) = s i g n ( w T x + b ) f(x)=sign(w^Tx+b) f(x)=sign(wTx+b)是一个经典判别模型。
二、SVM基本型推导
SVM也叫最大间隔分类器,定义模型为:
m a x m a r g i n ( w , b ) = m a x d i s t a n c e ( w , b , x i ) ( 1 ) s . t . { w T x i + b ≥ 0 , y i = + 1 w T x i + b ≤ 0 , y i = − 1 , i = 1 , 2 , . . . , m ( 2 ) max\ margin(w,b)=max\ distance(w,b,x_i) \qquad (1) \\ s.t.\left\{ \begin{aligned} w^Tx_i+b\ge 0,y_i=+1 \\ w^Tx_i+b \le 0,y_i=-1 \end{aligned} \right.,\ i=1,2,...,m\qquad (2) max margin(w,b)=max distance(w,b,xi)(1)s.t.{ wTxi+b≥0,yi=+1wTxi+b≤0,yi=−1, i=1,2,...,m(2)
通过将(2)伸缩变换可得:
s . t . { w T x i + b ≥ 1 , y i = + 1 w T x i + b ≤ − 1 , y i = − 1 ( 3 ) s.t.\left\{ \begin{aligned} w^Tx_i+b\ge 1,y_i=+1 \\ w^Tx_i+b \le -1,y_i=-1 \end{aligned}\qquad (3) \right. s.t.{ wTxi+b≥1,yi=+1wTxi+b≤−1,yi=−1(3)
设划分超平面上一点为x‘,则有 w T x ′ = − b ( 4 ) w^Tx'=-b\qquad (4) wTx′=−b(4)
距离公式:
r = ∣ w T ∣ ∣ w ∣ ∣ ( x − x ′ ) ∣ ( 投 影 ) = 1 ∣ ∣ w ∣ ∣ ∣ w T x + b ∣ ( 代 入 ( 4 ) 式 ) r=|\frac{w^T}{||w||}(x-x')|(投影)=\frac{1}{||w||}|w^Tx+b|(代入(4)式) r=∣∣∣w∣∣wT(x−x′)∣(投影)=∣∣w∣∣1∣wTx+b∣(代入(4)式)
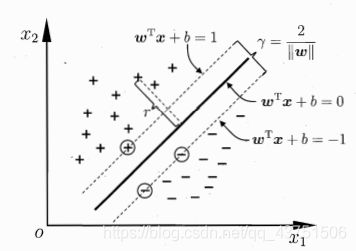
如图所示,距离超平面最近的这几个训练样本点使得(3)式等号成立,所以对于最近的点有 ∣ w T + b ∣ = 1 |w^T+b|=1 ∣wT+b∣=1,他们被称为”支持向量“,根据距离公式带入得:
r = 1 ∣ ∣ w ∣ ∣ ( 5 ) r=\frac1{||w||} \qquad(5) r=∣∣w∣∣1(5)
两个异类支持向量机到超平面的距离之和为:
γ = 2 ∣ ∣ w ∣ ∣ ( 6 ) \gamma =\frac2{||w||} \qquad(6) γ=∣∣w∣∣2(6)
它被称为间隔(margin).
想要找到最大间隔(maximum margin)的划分超平面,也就是找到满足(3)式种约束参数w和b,使得 γ \gamma γ最大,即
max w , b = 2 ∣ ∣ w ∣ ∣ s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , . . . , m ( 7 ) \begin{aligned} &\max\limits_{w,b}=\frac2{||w||}\\ &s.t. \ y_i(w^Tx_i+b)\ge1,i=1,2,...,m \end{aligned}\qquad(7) w,bmax=∣∣w∣∣2s.t. yi(wTxi+b)≥1,i=1,2,...,m(7)
显然最大化间隔,仅需要最大化 ∣ ∣ w ∣ ∣ − 1 ||w||^{-1} ∣∣w∣∣−1,这等价于最小化 ∣ ∣ w ∣ ∣ 2 ||w||^{2} ∣∣w∣∣2,于是(7)式重写为
min w , b = 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , . . . , m ( 8 ) \begin{aligned} &\min\limits_{w,b}=\frac1{2}{||w||}^2\\ &s.t. \ y_i(w^Tx_i+b)\ge1,i=1,2,...,m \end{aligned}\qquad(8) w,bmin=21∣∣w∣∣2s.t. yi(wTxi+b)≥1,i=1,2,...,m(8)
(8)式即为SVM的基本型