机器学习笔记（三）—— 二向箔（从PCA到SVD）

还记得《三体》中的“二向箔”吗？那种降维打击真的令人印象深刻！“我毁灭你，与你何干！”我想这应该算是所有科幻小说中排的上号的攻击手段了吧~
现在，我们有一个新的敌人，它有着庞大的身躯，有八双眼睛，4个头，10只手，20条腿，你无法用语言形容它，因为它巨大的让你难以一窥全貌，它的特点太多了让你无从找到描述的切入点 —— 是的，这就是横亘在机器学习路上的第一只拦路虎——数据集。
我常常有个疑惑，在几百兆甚至几十个G的数据集中，有着上百个特征属性，我们在模型学习过程中真的需要全部使用上吗？特征属性的数量越多，模型学习的效果真的更好吗？比如现在在波士顿的房价数据集中，你觉得波士顿的车辆数量会与房价的变化有太大的关系吗？也许我们在收集数据的时候，会尽可能地考虑更多的可能性，收集更多类型的数据，但是当我们开始进行模型学习的时候，我们必须要把它当成一盘丰盛的食材，去细心的肢解它，取其精华，去其糟粕。
那么我们该如何对待这令人抓狂的敌人呢？我们是残忍而又狡猾的猎人，我们对待敌人绝不手软，我们要使用人类想象力所能想象到的极限攻击手段——降维打击去毁灭它！
现在，让我来隆重地向你们介绍，机器学习中的二向箔 —— 主成分分析法（PCA） & 奇异值分解法（SVD）！！！

一、主成分分析法

主成分分析法（Principal Component Analysis)是最常用的几种降维方法之一。PCA的思想是将原有的n维数据集映射到全新的具有正交特征的K维上。那么，我们如何得到这全新的K维空间呢？有两种思路：分别是对应于样本到超平面的最小投影距离以及样本点在超平面上的投影点的最大方差

（一）PCA的推导

1.1 最小投影距离

在原先的n维空间中有大量的样本点，但是我希望现在只用一个超平面来对这所有的样本点进行恰当的表达（这一过程你可以理解为二维坐标中的点投影在一根直线上、三维坐标中的点投影在一个面上）。首先我脑海中想到的是基于我们最小二乘法思想的最近投影距离。

为了方便计算，首先我们要对m个n维样本$(x^{(1)},.....,x^{(m)})$进行中心化操作，使其${\sum }_{i=1}^m{x}^{(i)}=0$ ; 接着假设投影变换后的新坐标系（PS：记住这是坐标系，不是指数据点新的坐标）为$({\omega }_1,....,{\omega }_n)$，其中$\omega$是标准正交基，即$||\omega ||=1$,${\omega }_i^T{\omega }_j=0$

假设现在将维度降低至$n^{\prime }<n$, 则样本点$x^{(i)}$ 在低维左边下的投影为$z^{(i)}=(z_1^{(i)},z_2^{(i)},....,z_{n^{\prime }}^{(i)}{)}^T$,其中$z_j^{(i)}={\omega }_j^T{x}^{(i)}$ 是$x^{(i)}$低维坐标下第$j$维的坐标。

好了，现在我们有最原始的数据集$x^{(i)}$, 也有降维后的数据集$z^{(i)}$, 也有了新的坐标系$\omega$ , 现在我们试图将低维的数据重新恢复至n维的$X^{(i)}={\sum }_{j=1}^{n^{\prime }}{z}_j^{(i)}{w}_j=W{z}^{(i)}$ ,注 ： $W=({\omega }_1,....,{\omega }_{n^{\prime }})$

因此，为了使所有的样本到超平面的距离足够近，我们需要最小化下面的式子：$$\sum _{i=1}^m||X^{(i)}-x^{(i)}|{|}^2$$
即：

${\sum }_{i=1}^m||X^{(i)}-x^{(i)}|{|}^2$

$={\sum }_{i=1}^m||W{z}^{(i)}-x^{(i)}|{|}^2$

$={\sum }_{i=1}^m(W{z}^{(i)}{)}^T(W{z}^{(i)})-2{\sum }_{i=1}^m(W{z}^{(i)}{)}^T{x}^{(i)}+{\sum }_{i=1}^m{x}^{(i)T}{x}^{(i)}$

$={\sum }_{i=1}^m(z^{(i)}{)}^T(z^{(i)})-2{\sum }_{i=1}^m{z}^{(i)T}{W}^T{x}^{(i)}+{\sum }_{i=1}^m{x}^{(i)T}{x}^{(i)}$

$={\sum }_{i=1}^m(z^{(i)}{)}^T(z^{(i)})-2{\sum }_{i=1}^m{z}^{(i)T}{x}^{(i)}+{\sum }_{i=1}^m{x}^{(i)T}{x}^{(i)}$

$=-{\sum }_{i=1}^m{z}^{(i)T}{x}^{(i)}+{\sum }_{i=1}^m{x}^{(i)T}{x}^{(i)}$

$=-tr(W^T({\sum }_{i=1}^m{x}^{(i)}{x}^{(i)T})W)+{\sum }_{i=1}^m{x}^{(i)T}{x}^{(i)}$

$=-tr(W^{T}X{X}^{T}W)+{\sum }_{i=1}^m{x}^{(i)T}{x}^{(i)}$

由于在上式中${\sum }_{i=1}^m{x}^{(i)T}{x}^{(i)}$是一个常量，因此最小化${\sum }_{i=1}^m||X^{(i)}-x^{(i)}|{|}^2$ 等价于最大化$$tr(W^{T}X{X}^{T}W)$$ $$s.t.W^{T}W=I$$
利用拉格朗日函数可以得到：
$$J(W)=tr(W^{T}X{X}^{T}W+\lambda (W^{T}W-I))$$
通过 $$\frac{\partial J(W)}{\partial W}=0$$
解：
$$X{X}^{T}W=\lambda W$$
也就是$W$ 是$X{X}^T$的$n^{\prime }$个特征向量组成的矩阵，特征值$\lambda$的值的大小代表对应的特征向量上所能表达的数据的信息量的多少，简单来说，$\lambda$的值越大，特征向量方向上能够表达的数据信息越多，越能代表原始数据！所以，对于原始数据集，通过对$\lambda$的值从大到小进行排序，取其中前$n^{\prime }$个特征值所对应的特征向量构成$W$，我们只需要使用$z^{(i)}=W^T{x}^{(i)}$，就可以将其降维至基于最小投影距离的新的$n^{\prime }$维的数据集了。

1.2 最大方差法

首先我们需要明确一下，为什么要使用样本点在超平面上具有最大方差时比较好。现在有$F_1、F_2$两个方向，可以很明显地看出在$F_1$轴上数据点的投影较分散（方差较大），在$F_2$上地数据点的投影较紧凑（方差较小），在相信我们直觉的情况下，我们本能地会认为$F_1$轴上的投影点能够保存更多的原始数据集的信息。信息论中认为信号具有较大的方差，噪声具有较小的方差，信号与噪声的方差比（信噪比）越大越好。因此$F_1$轴就是我们的主成分，而$F_2$轴就是我们的噪声；这种思想我们可以推广到n维空间中。对于n维数据样本，首先我们求出基于最大方差的第一主成分，然后将数据集去掉第一主成分的分量构成新的数据集去求第二主成分，一直到求出第d个 (PS:我们需要的维数) 主成分为止！

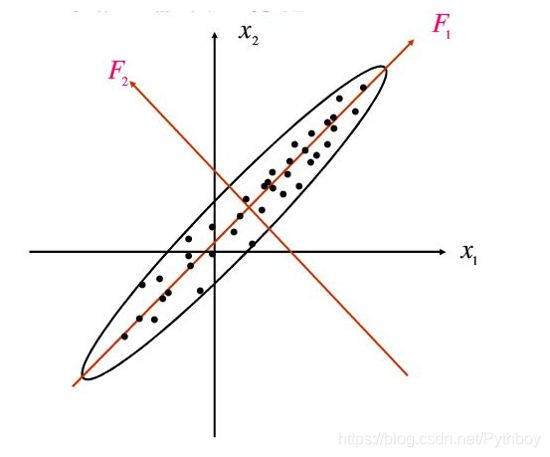
在1.1的推导中我们已经直到样本点$x^{(i)}$在新的坐标系上的投影为$W^T{x}^{(i)}$，因此要使所有的样本的投影方差最大，即最大化：$$\sum _{i=1}^m{W}^T{x}^{(i)}{x}^{(i)T}W$$ $$s.t.W^{T}W=I$$
因此最后结果依然为：
$$X{X}^{T}W=\lambda W$$
解释如上！也是就是说，通过对数据集样本的协方差矩阵$X{X}^T$进行特征集分解，取最大$n^{\prime }$个特征值所对应的特征向量作为投影矩阵，不仅可以得到最小投影距离，而且可以得到最大投影方差，可谓一石二鸟，一举两得！！???

现在我们来回想一下我们为什么要降维？对于庞大的数据集过多的特征，我们的学习模型有时候会充分学习到那些无关紧要的特征，从而会导致过拟合现象。那么如果在繁杂的特征中判别哪些信息是有用的，需要被学习的；哪些信息是垃圾信息，会对学习模型产生不利影响，那么我们的学习模型的效用将会大大的提高！而这就是我们PCA要做到的事情，这就是我们的新维数d所能产生的巨大影响。上面提到过，$\lambda$的值的大小代表了那个特征向量上多能记载的信息量的多少，因此通过$\frac{{\sum }_{i=1}^d{\lambda }_i}{{\sum }_{i=1}^n{\lambda }_i}\ast 100\%$的大小，可以了解到新的d维数据集能够表达出初始输出集多少信息。

（二）算法描述

PCA算法的数学描述
伪代码：

'''
输入： 样本集 D :m个样本,n维 ； 低维空间维数d

过程：
1. 对所有的样本进行中心化操作
2. 计算样本的协方差矩阵
3. 对协方差矩阵做特征值分解
4. 取最大的d个特征值所对应的特征向量作为投影矩阵
5. 利用投影矩阵获得新的d维数据样本

输出：
投影矩阵W ； 新的d维数据集样本
'''

核心代码：

def PCA(dataset,d):
	MeanDataset = dataset - np.mean(dataset,axis = 0) ; #中心化操作
	CovMat = np.(MeanDataset,rowvar = 0);  #求协方差矩阵
	Vals,Vects = np.linalg.eig(np.mat(CovMat)) ; #求特征值与特征向量
	NewSort = argsort(Vals) ; # 从小到大排序
	NewSort = Newsort[::-1];#从大到小排序
	Vects = Vects[:,Newsort[:d]]; #选取前d个最大的特征值所代表的特征向量
	LowDataset = MeanDataset * Vects; #新的d维数据样本
	return LowDataset,Vects; 

好了，现在我们通过上面简单的代码就实现了主成分分析过程。但是你是否会有疑惑，我们在线性回归模型中踢掉了最小二乘法所代表的矩阵计算，而选择了梯度下降法，目的就是为了能够减轻计算 ； 而主成分分析法实现降维的目的也是为了能够减小数据集的量级，从而能够减少计算 ； 现在在主成分分析模型中，我们却被迫采用了令人头疼的矩阵计算，真的合适吗？还有没有更好的解决办法？
在回归的“二三事”中我曾提到过梯度上升法，这里我们将再次拾起梯度法来踢走令人生厌的超规模矩阵计算。

（三） PCA的梯度上升法实现

现在我们基于最大投影方差，我们先求第一主成分：
第一步： 中心化处理
$$\sum _{i=1}^m{x}_i=0$$
第二步：确定效益函数
设 $$W=({\omega }_1,....,{\omega }_n{)}^T$$
则方差为：$$Var(X_{pricipal})=\frac{1}{m}\sum _{i=1}^m(X_{pricipal}^{(i)}-X_{mean}{)}^2=\frac{1}{m}\sum _{i=1}^m||X_{pricipal}^{(i)}-X_{mean}|{|}^2$$
由于已经中心化处理过,故：
$$Var(X_{pricipal})=\frac{1}{m}\sum _{i=1}^m||X_{pricipal}^{(i)}|{|}^2=\frac{1}{m}\sum _{i=1}^m||X^{(i)}{\omega }_i|{|}^2$$
即我们的目标变为，求w值，使得：
$$max:f(x)=\frac{1}{m}\sum _{i=1}^m||X^{(i)}{\omega }_i|{|}^2=\frac{1}{m}\sum _{i=1}^m(X_1^{(1)}{\omega }_1+....+X_1^{(n)}{\omega }_n{)}^2$$
第三步：求梯度
$$\nabla f=(\frac{\partial f}{\partial {\omega }_1},.....,\frac{\partial f}{\partial {\omega }_n}{)}^T=\frac{2}{m}(\sum _{i=1}^m(X^{(i)}W)X_1^{(i)},......,\sum _{i=1}^m(X^{(i)}W)X_n^{(i)}{)}^T$$
通过化简得：
$$\nabla f=\frac{2}{m}{X}^T(XW)$$
第四步：更新W，求得效益函数极大值，获得第一主成分
$$W_{new}=W_{old}+\alpha \nabla f$$

现在我们已经获得了想要得第一主成分，也就是通过它我们已经可以实现将n维数据降维至1维空间上了 ； 但是单独得1维数据在很多情况下并不能满足表达原始数据集绝大多数信息得要求，因此如何获得其他d-1维的数据是我们接下来的工作：

第一步：求出主成分上面的数据
$$X_{new}=X_{old}-X_{old}W$$
即通过基础的矩阵运算，我们就可以得到去除主成分分量后的新的数据集了
第二步：在新的数据集是继续求主成分，方法与上面一样
第三步：重复上面操作，直至得到d个主成分

代码：

class PCA:

    def __init__(self, n_components):
        """初始化PCA"""
        assert n_components >= 1, "n_components must be valid"
        self.n_components = n_components #主成分个数
        self.components_ = None ##投影矩阵

    def fit(self, X, eta=0.01, n_iters=1e4):
        """获得数据集X的前n个主成分"""
        assert self.n_components <= X.shape[1], \
            "n_components must not be greater than the feature number of X"

        def demean(X): #中心化操作
            return X - np.mean(X, axis=0) 

        def f(w, X):
            return np.sum((X.dot(w) ** 2)) / len(X)

        def df(w, X): #梯度
            return X.T.dot(X.dot(w)) * 2. / len(X)

        def direction(w): #标准化方向向量
            return w / np.linalg.norm(w)

        def first_component(X, initial_w, eta=0.01, n_iters=1e4, epsilon=1e-8): #求主成分的过程

            w = direction(initial_w)
            cur_iter = 0

            while cur_iter < n_iters: #梯度上升过程
                gradient = df(w, X)
                last_w = w
                w = w + eta * gradient
                w = direction(w)
                if (abs(f(w, X) - f(last_w, X)) < epsilon):
                    break

                cur_iter += 1

            return w

        X_pca = demean(X)
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))  #初始化投影矩阵
        for i in range(self.n_components): #求d维投影矩阵
            initial_w = np.random.random(X_pca.shape[1])
            w = first_component(X_pca, initial_w, eta, n_iters)
            self.components_[i,:] = w

            X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w

        return self

    def transform(self, X):
        """将给定的X，映射到各个主成分分量中"""
        assert X.shape[1] == self.components_.shape[1]

        return X.dot(self.components_.T)

    def inverse_transform(self, X):
        """将给定的X，反向映射回原来的特征空间"""
        assert X.shape[1] == self.components_.shape[0]

        return X.dot(self.components_)

    def __repr__(self):
        return "PCA(n_components=%d)" % self.n_components

二、奇异值分解

在主成分分析一部分我们提到，使用PCA进行降维，需要找到样本的协方差矩阵$X^{T}X$的最大的$d$个特征值，然后用其对应的特征向量作为投影矩阵进行降维。但是当样本数量很多、特征数很大的时候，求出协方差矩阵是一件计算量十分巨大的工程，对此我是类比线性模型的推导过程，给出梯度上升法来简化学习过程。事实上，我们还有另一种工具——奇异值分解（SVD），同样可以得到得到协方差$X^{T}X$的d维投影矩阵，且并不需要求出协方差矩阵。这种方法在样本量大的时候十分有效，实际上在sklearn库中的PCA算法使用的就是SVD算法。下面我们来一窥全貌！

（一）什么是SVD

对于一个方阵A(N x N矩阵），其特征值与特征向量的定义维：
$$Ax=\lambda x$$
令$\Omega ={\omega }_1,....,{\omega }_n$为特征向量组成的矩阵，$T$为以n个特征值为主对角线的N x N矩阵，则：
$$A=\Omega \Sigma {\Omega }^{-1}$$
通过将$\Omega$的n个特征向量标准正交化，使其满足$||{\omega }_1||=1$ 且 ${\Omega }^T\Omega =I$，则$$A=\Omega \Sigma {\Omega }^T$$
但是上面的情况必须要满足A为方阵的前提条件，那么对于M x N 的非方阵矩阵，我们可以对其进行分解吗？SVD干的就是这个事 —— SVD是适用于任意形式的矩阵的一种分解方法！！！

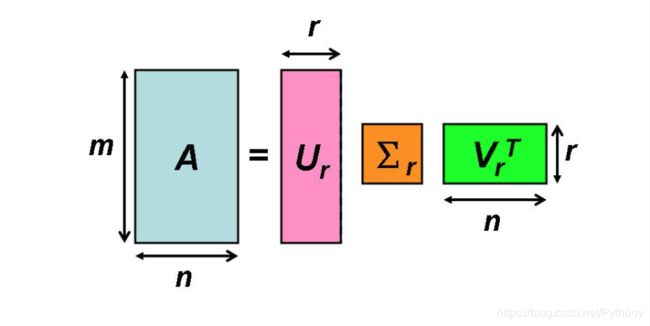
假设A是一个[M,N]的矩阵，那么我们可以得到一个[M,M]的矩阵$U$(里面的向量都是正交的，称为左奇异向量)，一个[M,N]的矩阵$T$(除了主对角线都是零，主对角线上为奇异值），一个[N,N]的矩阵$V^T$(里面的向量都正交，称为右奇异向量），则：
$$A=U\Sigma V^T$$

现在来了，我们该如何去求左奇异向量、右奇异向量、奇异值呢？

观察一下，右奇异向量的维数是N x N维，而$A^{T}A$也是N x N维，那么我们对$A^{T}A$做特征分解试试看：
$$(A^{T}A)v_i={\lambda }_i{v}_i$$
如果我们将$A^{T}A$的每个特征向量组成一个N x N的矩阵V，那么它就构成了我们的右奇异矩阵；
证明：
由于$$A=U\Sigma V^T,A^T=V{\Sigma }^T{U}^T$$
则：$$A^{T}A=V{\Sigma }^T{U}^{T}U\Sigma V^T$$
由于:$$U^{T}U=I,{\Sigma }^T\Sigma ={\Sigma }^2$$
则：$$A^{T}A=V{\Sigma }^2{V}^T$$
证毕！

现在，我们使用相同的方法去求左奇异矩阵：
$$(A{A}^T)u_i={\lambda }_i{u}_i$$
我们将$A{A}^T$的所有特征向量构成一个M x M的矩阵U，就是我们的左奇异矩阵U了。
$A{A}^T=U{T}^2{U}^T$可以证明U是我们想要的左奇异矩阵！

现在我们需要去求奇异值矩阵$\Sigma$了
由于：$$AV=U\Sigma V^{T}V=U\Sigma$$
得：
$$A{v}_i={\sigma }_i{u}_i$$
即对于每一个奇异值$\sigma$，我们可以通过${\sigma }_i=\frac{A{v}_i}{u_i}$求得(注：$v_i$是V的特征向量，$u_i$是U的特征向量）

注意，在上面我们证明右奇异矩阵V的时候，说到$A^{T}A=V{\Sigma }^2{V}^T$，那么${\Sigma }^2$主对角线上的奇异值不就是$A^{T}A$的特征值嘛！
所以我们右更简单的求解奇异值的方法：
$${\sigma }_i=\sqrt{{\lambda }_i}$$
其中$\lambda$是$A^{T}A$的特征值。
同理：
由$A{v}_i={\sigma }_i{u}_i$可得：
$$u_i=\frac{1}{{\sigma }_i}A{v}_i$$
是不是又可以减轻U矩阵的计算量啦~~~

这时候各位看客肯定会跳出来吐槽我，说好的可以通过SVD来降低矩阵计算量的呀，你这个$O(N^3)$的算法，更复杂了好吗？
是这样没错，如果没有Google的SVD并行化算法的话，那么确实处理上亿规模的矩阵运算一定是天方夜谈，但是在众多大牛的贡献下，SVD的并行化计算也有成熟的代码或框架供大家使用，所以通过SVD去求解$A{A}^T$的特征向量即PCA所要的协方差矩阵是一件更为取巧的事情！

（二）SVD与PCA

我们花了大力气去实现SVD，它有什么特性使我们如此着迷呢？
在奇异值矩阵中，我们按照奇异值的大小从大到小进行排列，会发现奇异值减小的特别快，在很多情况下，前10%的奇异值的和就可以占到全部奇异值之和99%以上的比例！这意味着什么？意味着我们可以将维数降低到原来的十分之一还可以解释其99%以上的信息，这是多么的令人着迷~
也就是我们通过最大的k个奇异值与其对应的左右奇异向量就可以近似描述我们原来的矩阵，即：
$$A_{m\ast n}=U_{m\ast m}{\Sigma }_{m\ast n}{V}_{n\ast n}^T=U_{m\ast k}{\Sigma }_{k\ast k}{V}_{k\ast n}^T$$

因此，SVD不仅仅可以用作PCA降维过程中，而且可以用作数据压缩、去噪等过程。这是一件多么有趣的事情！