动态规划
文章目录
-
- 1. 概念
- 2. 解题方法
- 3. 补充例题——摆动序列
1. 概念
什么是动态规划?其实就是求全局解最优解的过程。与其类似的有贪心算法,但贪心算法是专注于求局部情况的最优解,动态规划是专注于全局的最优解。
它的概念其实我也讲不出所以然,大家意会即可。它的关键词是变化,动态规划的题的状态是在不断变化的,贪心算法也是同理,但求局部最优解的就是贪心,求全局最优解的就是动态规划。
下面了解下动态规划的一些概念,这将有助于我们了解动态规划的解法,简单看就可以了不必深究,会有些抽象,当然也可以看完下面的内容后再回头来看这里,就会有更容易理解了:
-
阶段:把所给求解问题的过程恰当地分成若干个相互联系的阶段,以便于求解,过程不同,阶段数就可能不同。描述阶段的变量称为阶段变量。在多数情况下,阶段变量是离散的,用k表示。此外,也有阶段变量是连续的情形。如果过程可以在任何时刻作出决策,且在任意两个不同的时刻之间允许有无穷多个决策时,阶段变量就是连续的
-
状态:状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。
-
无后效性:某一个阶段的状态只受前一阶段状态的影响,而不受别的阶段状态的影响。这一点很重要,要了解清楚。
-
决策:一个阶段的状态给定以后,从该状态演变到下一阶段某个状态的一种选择(行动)称为决策。在最优控制中,也称为控制。在许多问题中,决策可以自然而然地表示为一个数或一组数。不同的决策对应着不同的数值。描述决策的变量称决策变量,因状态满足无后效性,故在每个阶段选择决策时只需考虑当前的状态而无须考虑过程的历史 ,决策变量的范围称为允许决策集合。
-
策略:由每个阶段的决策组成的序列称为策略。对于每一个实际的多阶段决策过程,可供选取的策略有一定的范围限制,这个范围称为允许策略集合,允许策略集合中达到最优效果的策略称为最优策略。这个策略也就是状态转移方程。
2. 解题方法
动态规划首先需要我们定义状态是什么,然后根据题意,写出状态转移方程。下面我们以一道leetcode题为例,讲解一下,该题是978.最长湍流子数组
当 A 的子数组 A[i], A[i+1], …, A[j] 满足下列条件时,我们称其为湍流子数组:
1.若 i <= k < j,当 k 为奇数时, A[k] > A[k+1],且当 k 为偶数时,A[k] < A[k+1];
2.若 i <= k < j,当 k 为偶数时,A[k] > A[k+1] ,且当 k 为奇数时, A[k] < A[k+1]。
也就是说,如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是湍流子数组。返回 A 的最大湍流子数组的长度。
示例 1:
输入:[9,4,2,10,7,8,8,1,9]
输出:5
解释:(A[1] > A[2] < A[3] > A[4] < A[5])
示例 2:
输入:[4,8,12,16]
输出:2
示例 3:
输入:[100]
输出:1
从这道题我们可以得出有两个情况,一个是上升,一个是下降,所以我们定义两个状态:
- 定义 up[i] 表示以位置 i 结尾的,并且 arr[i - 1] < arr[i] 的最长湍流子数组长度。
- 定义 down[i] 表示以位置 i 结尾的,并且 arr[i - 1] > arr[i] 的最长湍流子数组长度。
两个数组初始化都是1,因为每个数字本身都是一个最小的湍流子数组。当然这里定义成数组是因为比较好理解,后面也可以进行优化成一个变量,这里先不说。下面来写出状态转移方程:
- up[i] = down[i - 1] + 1,当 arr[i - 1] < arr[i];
- down[i] = up[i - 1] + 1,当 arr[i - 1] > arr[i];
这个又是怎么求出来的呢?大家看图吧,然后自己列一下三个数组,分析下关系应该就写的出来了:图片描述
所以大概就是这样,再总结下做题过程:分析出状态,写状态转移方程。下面贴一下这道题的Java代码,我的代码就把数组简化成一个变量了,节省了空间:
class Solution {
public int maxTurbulenceSize(int[] nums) {
int down = 1, up = 1;
int ans = 1;
for (int i = 1; i < nums.length; i++) {
if (nums[i] > nums[i - 1]){
up = down + 1;
down = 1;
}
else if (nums[i] < nums[i - 1]){
down = up + 1;
up = 1;
}
else{
up = down = 1;
}
ans = Math.max(ans,Math.max(up,down));
}
return ans;
}
}
3. 补充例题——摆动序列
先来看下题意:
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。
示例 2:
输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
示例 3:
输入: [1,2,3,4,5,6,7,8,9]
输出: 2
这道题和上面那道题其实上是一样的,只不过这里的状态是可以延续下去的,所以我们继续列出两个状态数组:up[i]和down[i]。
写成状态转移方程:
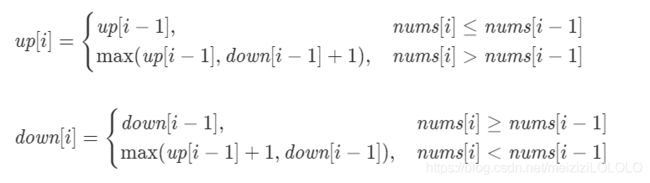
下面就是我的Java代码,我也依旧把数组简化成了变量:
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
if (n < 2) {
return n;
}
int up = 1, down = 1;
for (int i = 1; i < n; i++) {
if (nums[i] > nums[i - 1]) {
up = Math.max(up, down + 1);
} else if (nums[i] < nums[i - 1]) {
down = Math.max(up + 1, down);
}
}
return Math.max(up, down);
}
}