Python----数据分析-使用scikit-learn构建模型实训（wine数据集、wine_quality数据）

Python----数据分析-使用scikit-learn构建模型实训（wine数据集、wine_quality数据）

---

目录：

实训1 使用 sklearn处理wine和wine_quality数据集
实训2 构建基于wine数据集的k- Means聚类模型
实训3 构建基于wine数据集的SVM分类模型
实训4 构建基于wine_quality数据集的回归模型

---

wine数据集包含来自3种不同起源的葡萄酒的共178条记录。13个属性是葡萄酒的13种化学成分。通过化学分析可以来推断葡萄酒的起源。值得一提的是所有属性变量都是连续变量。

---

实训1 使用 sklearn处理wine和wine_quality数据集

1.训练要点

• 掌握 sklearn转换器的用法。
• 掌握训练集、测试集划分的方法。
• 掌握使用sklearn进行PCA降维的方法。

2.需求说明

• wine数据集和 winequality数据集是两份和酒有关的数据集。wine数据集包含3种 同起源的葡萄酒的记录,共178条。其中,每个特征对应葡萄酒的每种化学成分,并且都 属于连续型数据。通过化学分析可以推断葡萄酒的起源。
• winequality数据集共有4898个观察值,11个输入特征和一个标签。其中,不同类的
  观察值数量不等,所有特征为连续型数据。通过酒的各类化学成分,预测该葡萄酒的评分

3.实现思路及步骤

• 使用pandas库分别读取wine数据集和 winquality数据集
• 将wine数据集和winequality数据集的数据和标签拆分开(提取)。
• 将winequality数据集划分为训练集和测试集。
• 标准化wine数据集和 wine quality数据集
• 对wine数据集和 winequality数据集进行PCA降维。

---

import pandas as pd

// 读取数据
wine_quality = pd.read_csv('data/winequality.csv',sep=';')
wine = pd.read_csv('data/wine.csv')
print(type(wine),type(wine_quality))
// 

// 提取 wine_quality 数据
wine_quality_data = wine_quality.iloc[:,:-1]
wine_quality_target = wine_quality['quality']
// 提取 wine 数据
wine_data = wine.iloc[:,:-1]
wine_target = wine['Class']

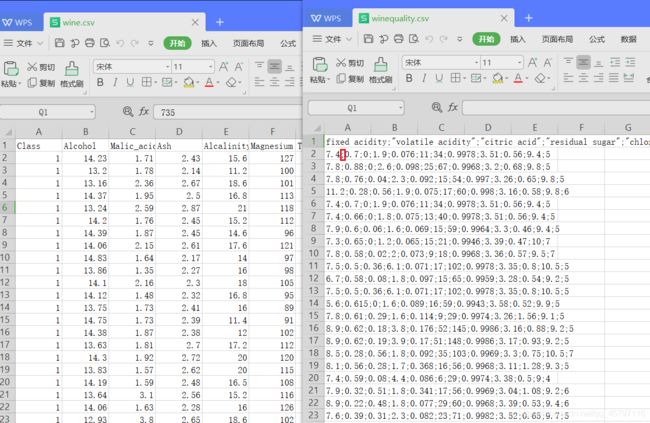
wine数据集和winequality数据集的表现形式不一样，这里的wine数据集可以直接读入，而winequality数据集在文件中是以”；”为间隔的，所以要采用间隔读入的方式获取其数据。读取后数据都以DataFrame的类型保留，使用iloc等切片操作提取所需数据。

// 将 wine_quality 数据划分为训练集和测试集
from sklearn.model_selection import train_test_split

wine_quality_data_train,wine_quality_data_test,\
wine_quality_target_train,wine_quality_target_test=\
train_test_split(wine_quality_data,wine_quality_target,test_size=0.2,random_state=321)

wine_data_train,wine_data_test,\
wine_target_train,wine_target_test=\
train_test_split(wine_data,wine_target,test_size=0.2,random_state=321)

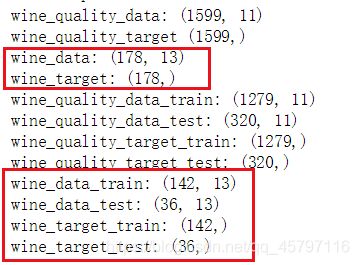
train_test_split（）函数将数据集划分为训练集和测试集两部分，参数test_size=0.2代表着测试集在总数中的占比，通过计算wine_data总共178条记录，wine_data_test有36条，占0.20224171(20%),参数random_state=321，表示随机种子编号，方便测试时得到相同随机结果。

// 标准化数据集
from sklearn.preprocessing import StandardScaler

stdScaler = StandardScaler().fit(wine_data_train) // 生成标准化规则
wine_trainScaler = stdScaler.transform(wine_data_train) // 对训练集标准化
wine_testScaler = stdScaler.transform(wine_data_test) // 用训练集建立的模型对测试集标准化

Scaler = StandardScaler().fit(wine_quality_data_train) // 生成标准化规则
winequality_trainScaler = Scaler.transform(wine_quality_data_train) // 对训练集标准化
winequality_testScaler = Scaler.transform(wine_quality_data_test) // 用训练集建立的模型对测试集标准化

这里有个顺序：生成标准化规则；对训练集标准化；用训练集建立的模型对测试集标准化
主要是因为在数据分析的时候，各类特征处理相关的操作都需要对训练集和测试集分开进行，同时需要将训练集的操作规则、权重系数等应用到测试集中。这也就是为什么生成规则时fit传入训练集。transform函数紧接着将定义好的规则应用对传入的特征进行对应转换。

// PCA降维
from sklearn.decomposition import PCA

pca_model = PCA(n_components=5).fit(wine_trainScaler) // 生成PCA规则
wine_trainpca = pca_model.transform(wine_trainScaler) // 将规则应用到训练集
wine_testpca = pca_model.transform(wine_testScaler)   // 将规则应用到测试集 

pca_model = PCA(n_components=5).fit(winequality_trainScaler) // 生成PCA规则
winequality_trainpca = pca_model.transform(winequality_trainScaler) // 将规则应用到训练集
winequality_testpca = pca_model.transform(winequality_testScaler)   #// 将规则应用到测试集

PCA(n_components=5)的参数n_components表示将原始数据降低到n个维度。

返回顶部

---

实训2 构建基于wine数据集的k- Means聚类模型

1.训练要点

• 了解sklearn估计器的用法。
• 掌握聚类模型的构建方法。
• 掌握聚类模型的评价方法。

2.需求说明

• wine数据集的葡萄酒总共分为3种,通过将wine数据集的数据进行聚类,聚集为3 个簇,能够实现葡萄酒的类别划分。

3.实现思路及步骤

• 根据实训1的wine数据集处理的结果,构建聚类数目为3的- -Means模型。
• 对比真实标签和聚类标签求取FMI。
• 在聚类数目为2~10类时,确定最优聚类数目。
• 求取模型的轮廓系数,绘制轮廓系数折线图,确定最优聚类数目。
• 求取 Calinski-Harabasz-指数,确定最优聚类数目。

// 构建 K-Means 模型
from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=3,random_state=32).fit(wine_trainScaler) //构建训练模型
print('wine_trainScaler构建的模型为：\n',kmeans)
//wine_trainScaler构建的模型为：
 KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
       n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
       random_state=32, tol=0.0001, verbose=0)

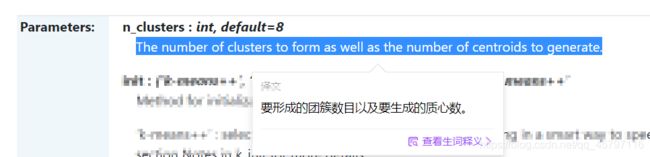
构建K-Means聚类模型，参数n_clusters=3表示要形成的团簇数目，也就是分为几类，这里是分为3类。

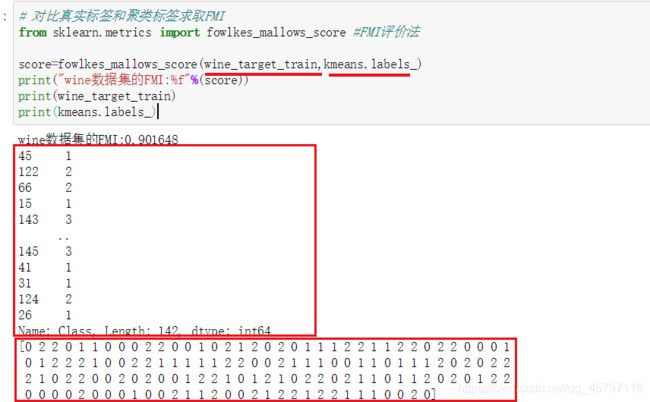
// 对比真实标签和聚类标签求取FMI
from sklearn.metrics import fowlkes_mallows_score //FMI评价法

score=fowlkes_mallows_score(wine_target_train,kmeans.labels_)
print("wine数据集的FMI:%f"%(score))
//wine数据集的FMI:0.901648

//在聚类数目为2~10类时,确定最优聚类数目
from sklearn.metrics import fowlkes_mallows_score
from sklearn.cluster import KMeans

for i in range(2,11):
    kmeans = KMeans(n_clusters=i,random_state=32).fit(wine_trainScaler)
    score = fowlkes_mallows_score(wine_target_train,kmeans.labels_)
    print('wine聚%d类FMI评价分为：%f'%(i,score))

wine聚2类FMI评价分为：0.693972
wine聚3类FMI评价分为：0.901648
wine聚4类FMI评价分为：0.801280
wine聚5类FMI评价分为：0.775956
wine聚6类FMI评价分为：0.782225
wine聚7类FMI评价分为：0.607152
wine聚8类FMI评价分为：0.570184
wine聚9类FMI评价分为：0.567783
wine聚10类FMI评价分为：0.559720

// 求取模型的轮廓系数,绘制轮廓系数折线图,确定最优聚类数目
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
silhouettteScore = []
for i in range(2,11):
    // 构建并训练模型
    kmeans = KMeans(n_clusters = i,random_state=1).fit(wine)
    score = silhouette_score(wine,kmeans.labels_)
    silhouettteScore.append(score)
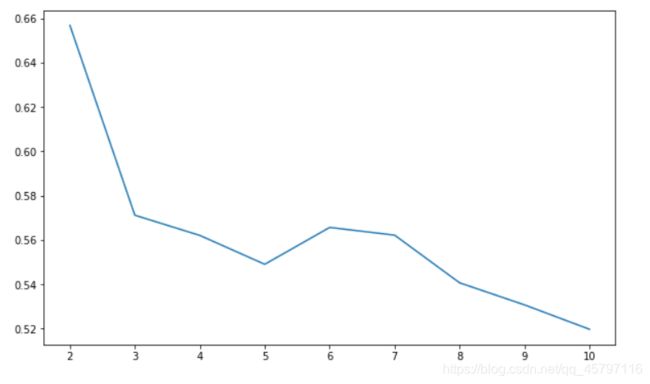
plt.figure(figsize=(10,6))
plt.plot(range(2,11),silhouettteScore,linewidth=1.5, linestyle="-")
plt.show()

求取模型的轮廓系数：

//求取 Calinski-Harabasz指数,确定最优聚类数
from sklearn.metrics import calinski_harabasz_score
for i in range(2,11):
    // 构建并训练模型
    kmeans = KMeans(n_clusters = i,random_state=1).fit(wine_trainScaler)
    score = calinski_harabaz_score(wine_trainScaler,kmeans.labels_)
    print('seeds数据聚%d类calinski_harabaz指数为：%f'%(i,score))

seeds数据聚2类calinski_harabaz指数为：67.189882
seeds数据聚3类calinski_harabaz指数为：62.785275
seeds数据聚4类calinski_harabaz指数为：49.058796
seeds数据聚5类calinski_harabaz指数为：41.101132
seeds数据聚6类calinski_harabaz指数为：36.321948
seeds数据聚7类calinski_harabaz指数为：34.295581
seeds数据聚8类calinski_harabaz指数为：31.101151
seeds数据聚9类calinski_harabaz指数为：28.693663
seeds数据聚10类calinski_harabaz指数为：28.563627

分析FMI评价分值，可以看出wine数据分3类的时候其FMI值最高，故聚类为3类的时候wine数据集K-means聚类效果最好
分析轮廓系数折线图，可以看出在wine数据集为3的时候，其平均畸变程度最大，故亦可知聚类为3类的时候效果最佳

返回顶部

---

实训3 构建基于wine数据集的SVM分类模型

1.训练要点

• 掌握sklearn估计器的用法。
• 掌握分类模型的构建方法。
• 掌握分类模型的评价方法。

2.需求说明

• wine数据集中的葡萄酒类别为3种,将wie数据集划分为训练集和测试集,使用训练 集训练SVM分类模型,并使用训练完成的模型预测测试集的葡萄酒类别归属。

3.实现思路及步骤

• 读取wine数据集,区分标签和数据。
• 将wine数据集划分为训练集和测试集
• 使用离差标准化方法标准化wine数据集。
• 构建SVM模型,并预测测试集结果。
• 打印出分类报告,评价分类模型性能。

import pandas as pd

// 读取数据
wine_quality = pd.read_csv('data/winequality.csv',sep=';')
wine = pd.read_csv('data/wine.csv')
// 提取 wine_quality 数据
wine_quality_data = wine_quality.iloc[:,:-1]
wine_quality_target = wine_quality['quality']
// 提取 wine 数据
wine_data = wine.iloc[:,:-1]
wine_target = wine['Class']

from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import MinMaxScaler

// 划分训练集、测试集
wine_data_train,wine_data_test,wine_target_train,wine_target_test=\
train_test_split(wine_data,wine_target,test_size=0.2,random_state=123)

// 数据标准化规则
Scaler = MinMaxScaler().fit(wine_data_train)
// 应用规则
wine_trainScaler = Scaler.transform(wine_data_train) // 对训练集进行标准化
wine_testScaler = Scaler.transform(wine_data_test)    // 用训练集训练的模型对测试集标准化

// 构建SVM分类模型
svm = SVC().fit(wine_trainScaler,wine_target_train)
print("建立的SVM模型为：\n",svm)
//建立的SVM模型为：
 SVC(C=1.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='scale', kernel='rbf',
    max_iter=-1, probability=False, random_state=None, shrinking=True,
    tol=0.001, verbose=False)
                                   
// 预测训练结果
wine_target_pred = svm.predict(wine_testScaler)   
print('预测前20个结果为：',wine_target_pred[:20])
//预测前20个结果为： [3 2 3 2 2 3 1 3 3 2 3 3 3 1 1 3 2 2 1 2]

// 打印模型评价报告
from sklearn.metrics import classification_report
print('使用SVM预测数据的分析报告为：\n',classification_report(wine_target_test,wine_target_pred))
//使用SVM预测数据的分析报告为：
               precision    recall  f1-score   support

           1       1.00      1.00      1.00         8
           2       1.00      1.00      1.00        11
           3       1.00      1.00      1.00        17

    accuracy                           1.00        36
   macro avg       1.00      1.00      1.00        36
weighted avg       1.00      1.00      1.00        36

返回顶部

---

实训4 构建基于wine_quality数据集的回归模型

1.训练要点
(1)熟练sklearn估计器的用法。
(2)掌握回归模型的构建方法。
(3)掌握回归模型的评价方法。

2.需求说明

• winequality数据集的葡萄酒评分在1~10之间,建线性回归模型与梯度提升回归模 型,训练 winequality数据集的训练集数据,训练完成后预测测试集的葡萄酒评分。结合 真实评分,评价构建的两个回归模型的好坏。

3.实现思路及步骤

• 根据winequality数据集处理的结果,构建线性回归模型。
• 根据wine quality数据集处理的结果,构建梯度提升回归模型。
• 结合真实评分和预测评分,计算均方误差中值绝对误差、可解释方差值。
• 根据得分,判定模型的性能优劣。

// 构建线性回归模型
from sklearn.linear_model import LinearRegression

clf = LinearRegression().fit(winequality_trainpca,wine_quality_target_train)
y_pred = clf.predict(winequality_testpca)
print('线性回归模型预测前10个结果为：','\n',y_pred[:10])
线性回归模型预测前10个结果为： 
 [5.27204611 5.16410891 6.93394979 6.52520955 5.56143289 5.02815869
 5.17867439 5.95768188 5.68991275 5.33085457]

// 根据wine_quality数据集处理的结果,构建梯度提升回归模型。
from sklearn.ensemble import GradientBoostingRegressor

gbr_wine = GradientBoostingRegressor().fit(winequality_trainpca,wine_quality_target_train)
wine_target_pred = gbr_wine.predict(winequality_testpca)
print('梯度提升回归模型预测前10个结果为：','\n',wine_target_pred[:10])
print('真实标签前10个预测结果为：','\n',list(wine_quality_target_test[:10]))
梯度提升回归模型预测前10个结果为： 
 [5.4569842  5.1020336  6.39325331 6.55163291 5.62504565 5.16770619
 5.22503393 5.6942301  5.43575267 5.22052962]
真实标签前10个预测结果为： 
 [6, 5, 6, 7, 6, 6, 5, 6, 6, 5]

from sklearn.metrics import mean_absolute_error,mean_squared_error,median_absolute_error,explained_variance_score,r2_score

print('线性回归模型评价结果：')
print('winequality数据线性回归模型的平均绝对误差为：',
     mean_absolute_error(wine_quality_target_test,y_pred))
print('winequality数据线性回归模型的均方误差为：',
     mean_squared_error(wine_quality_target_test,y_pred))
print('winequality数据线性回归模型的中值绝对误差为：',
     median_absolute_error(wine_quality_target_test,y_pred))
print('winequality数据线性回归模型的可解释方差值为：',
     explained_variance_score(wine_quality_target_test,y_pred))
print('winequality数据线性回归模型的R方值为：',
     r2_score(wine_quality_target_test,y_pred))

线性回归模型评价结果：
winequality数据线性回归模型的平均绝对误差为： 0.500442590483755
winequality数据线性回归模型的均方误差为： 0.4116335179704622
winequality数据线性回归模型的中值绝对误差为： 0.42681355355182804
winequality数据线性回归模型的可解释方差值为： 0.3304259967770349
winequality数据线性回归模型的R方值为： 0.32853409414296564

print('梯度提升回归模型评价结果：')
print('winequality数据梯度提升回归树模型的平均绝对误差为：',
     mean_absolute_error(wine_quality_target_test,wine_target_pred))
print('winequality数据梯度提升回归树模型的均方误差为：',
     mean_squared_error(wine_quality_target_test,wine_target_pred))
print('winequality数据梯度提升回归树模型的中值绝对误差为：',
     median_absolute_error(wine_quality_target_test,wine_target_pred))
print('winequality数据梯度提升回归树模型的可解释方差值为：',
     explained_variance_score(wine_quality_target_test,wine_target_pred))
print('winequality数据梯度提升回归树模型的R方值为：',
     r2_score(wine_quality_target_test,wine_target_pred))  

梯度提升回归模型评价结果：
winequality数据梯度提升回归树模型的平均绝对误差为： 0.49135412186249
winequality数据梯度提升回归树模型的均方误差为： 0.3929327053069297
winequality数据梯度提升回归树模型的中值绝对误差为： 0.4130905910176561
winequality数据梯度提升回归树模型的可解释方差值为： 0.3620462459660544
winequality数据梯度提升回归树模型的R方值为： 0.3590392827808905   

对于一个回归模型来说，平均绝对误差、均方误差、中值绝对误差越接近0越好，可解释方差和R2值越接近1越好。通过对比两者的回归评价指标不难发现，线性回归模型的平均绝对误差、均方误差、中值绝对误差都要大于梯度回归模型，但是可解释方差和R2值都要小于梯度回归模型。因此，梯度回归模型在五个指标上都要优于线性回归模型，故在本实训中，梯度回归模型性能更优！

返回顶部

---