计算机图形学 学习笔记(二):多边形扫描转换:X扫描线算法 和 改进的X扫描线算法
接上文 计算机图形学 学习笔记(一):概述,直线扫描算法:DDA,中点画线算法,Bresenham算法
光栅图形学算法
2.4 多边形扫描转换-X扫描线算法
多边形的扫描转换和区域填充这个问题是怎么样在离散的像素集上表示一个连续的二维图形?
多边形有两种重要的表示方法:顶点表示和点阵表示
顶点表示
顶点表示是用多边形的顶点序列来表示多边形。
优点:这种表示直观、几何意义强。占内存少、易于进行几何变化
缺点:但由于它没有明确指出哪些像素在多边形内,故不能直接用于面着色
点阵表示
点阵表示是用位于多边形内的像素几何来刻画多边形。
这种表示丢失了许多几何信息(如边界、顶点等),但它却是光栅显示系统时所需的表示形式
这涉及到两个问题:第一个问题是如果知道边界,能否求出哪些像素在多边形内?(可以)
第二个问题是知道多边形内部的像素,反过来如何求出边界?(不行)
光栅图形的一个基本问题是把多边形的顶点表示转化为点阵表示。这种转换称为多边形的扫描转换。
现在的问题是,知道多边形的边界,如何找到多边形内部的点,即把多边形内部填上颜色。
X-扫描线算法
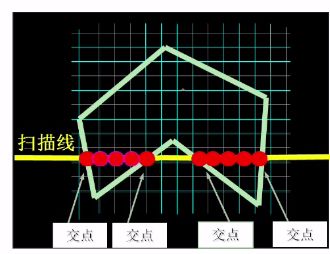
X-扫面线算法填充多边形的基本思想是按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的像素,即完成填充工作。
区间的端点可以通过计算扫描线与多边形边界线的交点获得。
算法的核心是按X递增顺序排列交点的X坐标序列。
由此,可得到X-扫描线算法步骤如下:
(1)确定多边形所占用的最大扫描线数,得到多边形顶点的最小和最大y值
(2)从y=y(min)到y=(ymax),每次用一条扫描线进行填充
(3)对一条扫描线填充的过程可以分为四个步骤
1. 求交:计算扫描线与多边形各边的交点
2. 排序:把所有交点按递增顺序进行排序
3. 交点配对:第一个与第二个,第三个与第四个
4. 区间填色:把这些相交区间内的像素置成不同于背景色的填充色
当扫描线与多边形顶点相交时,交点的取舍问题(交点的个数应保证为偶数个)
解决方案:
(1)若共享顶点的两条边分别落在扫描线的两边,交点只算一个
(2)若共享顶点的两条边在扫描线的同一边,这时交点作为零个或两个
检查共享顶点的两条边的另外两个端点的y值,按这两个y值中大于交点y值的个数来决定交点数
为了计算每条扫描线与多边形各边的交点,最简单的方法是把多边形的所有边放在一个表中。在处理每条扫描线时,按顺序从表中取出所有的边,分别与扫描线相交。
这个算法效率低,为什么?
关键问题是求交!而求交是很可怕的,求交的计算量是非常大的
2.5 多边形扫描转换-改进的X扫描线算法
扫描转换算法重要意义是提出了图形学里两个重要的思想:
(1)扫描线:当处理图形图像时按一条条扫描线处理
(2)增量的思想
求交点的时候能不能也采取增量的方法?每条扫描线的y值都知道,关键是求x的值。x是什么?
可以从三个方面考虑加以改进:
(1)在处理一条扫描线时,仅对与它相交的多边形的边(有效边)进行求交运算。
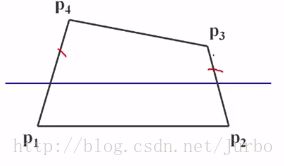
针对这条蓝色的扫描线,仅仅只有P1P4,P2P3这条边与它相交,因此这两条是有效边。在处理这条扫面线时,和它不相交的边就可以不考虑了。
(2)考虑扫描线的连贯性

蓝色的是当前的扫描线,红色是下一条扫描线。可以看出:当前扫描线与各边的交点顺序与下一条扫描线与各边的交点顺序很可能相同或非常相似。
(3)考虑多边形的连贯性
即当某条边与当前扫描线相交时,它很可能也下一条扫描线相交。
为了避免求交运算,需要引进一套特殊的数据结构。
活性边表(AET):
(1)活性边表(AET):把与当前扫描线相交的边称为活性边,并把它们按与扫描线交点 x 坐标递增的顺序 存放在一个链表 中。
(2)活性边表中的结点内容(一个结点在数据结构里可用结构来表示)

随着扫描线的移动,扫描线与多边形的交点和上一次交点是相关的,这意味着我们可以用增量来计算下一次扫描线的位置。
接下来证明下增量的值是多少:
增量的计算方式即斜率的倒数。
例子:
为了方便活性边表的建立与更新,需要构造一个特殊的数据结构即新边表(NET),用来存放多边形的边的信息,分为4个步骤
(1)首先构造一个纵向链表,链表的长度为多边形所占有的最大扫描线数,链表的每个结点,称为一个吊桶,对应多边形覆盖的每一条扫描线 。
(2)新边表(NET)挂在与该边低端 y 值相同的扫描线桶中。也就是说,存放在该扫描线第一次出现的边。

下面看一个新边表(NET)的例子:
可以看出这个多边形有10条扫描线,因此链表的长度为10。结点为1的地方,存放了第一条扫描线(y=1)经过的两条边 P1P2,P1P6 的信息。
每做一次新的扫描线时,要对已有的边进行三个处理:
- 查看是否是被除掉(我们只针对活性边进行处理)
- 如果不被去除(那么说明是活性边),就要对它的数据进行更新。所谓更新数据就是要更新它的 x 值,即:x+1/k
- 看看有没有新的边进来,新的边在新边表(NET)中,可以插入排序插进来
这个算法过程中没有求交,因为计算x值时,只计算了x的增量(即1/k),大大提高了效率。
算法描述
伪代码:
void polyfill(多边形 polygon,int color)
{
for(各条扫描线 i)
{
初始化 新边表头指针NET[i];
把y(min)=i 的边放进 新边表NET[i];
}
y=最低扫描线号;
初始化 活性边表AET 为空;
for(各条扫描线i)
{
把新边表NET[i]中的边结点用插入排序法插入 活性边表AET中,使之按 x 坐标定增顺序排列;
遍历活性边表AET,把配对交点区间(左闭区间右开区间)上的像素(x,y) 用 putpixel(x,y,color) 改写像素颜色值;
遍历活性边表AET,把y(max)=i 的结点从 活性边表AET中删除,并把 y(max)>i 结点的 x值 递增 Δx;
若允许多边形的边自相交,则用冒泡排序法对 活性边表AET 重新排序;
}
}多边形扫描转换算法小结
扫描线法可以实现已知任意多边形域边界的填充。
该填充算法(多边形扫描转换算法)是按扫描线的顺序,计算扫描线与待填充区域的相交区间,再用要求的颜色显示这些区间的像素,即完成填充工作。
为了提高算法效率:
- 我们引入了增量的思想
- 引入了连贯性思想
- 构建了一套特殊的数据结构(活性边表AET ,新边表 NET)
多边形扫描转换算法缺点:这里区间的端点通过计算扫描线与多边形边界的交点获得。所以待填充区域的边界线必须实现知道,因此它的缺点是无法实现对未知边界的区域填充。
解决这个问题的有几种算法:边缘填充算法,栅栏填充算法,边界标志算法
多边形扫描转换-边缘填充算法
基本思想是按任意顺序处理多边形的每条边。在处理每条边时,首先求出该边与扫描线的交点,然后将每一条扫描线上交点右方的所有像素取补。多边形的所有边处理完毕之后,填充即完成。
例子:
边缘填充算法,算法简单。但对于复杂图形,每一像素可能被访问多次,输入量和输出量比有效边算法大得多。
为了减少边缘填充法访问像素的次数,可以采用栅栏填充算法。
多边形扫描转换-栅栏填充算法
栅栏指的是一条过多边形顶点且与扫描线垂直的直线。它把多边形分为两半。在处理每条边与扫描线的交点时,将交点与栅栏之间的像素取补。
多边形扫描转换-边界标志算法
帧缓冲器中对多边形的每条边进行直线扫描转换,亦即对多边形边界所经过的像素当上标志。然后再采用和扫描线算法类似的方法将位于多边形内的各个区段着上所需的颜色。
由于边界标志算法不必建立维护边表以及对它进行排序,所以边界标志算法更适合硬件实现,它的执行速度比有序边表算法快一至两个数量级。