模拟退火算法解决起点固定的TSP问题(MATLAB)
(MATLAB)模拟退火算法解决起点固定的TSP问题
-
- 1. 问题描述
- 2. 程序修改思路
- 3. 程序运行结果
1. 问题描述
问题描述和解题思路请看我这篇博客:
https://blog.csdn.net/weixin_45727931/article/details/108110323
将该例题的题干再次复制下来:
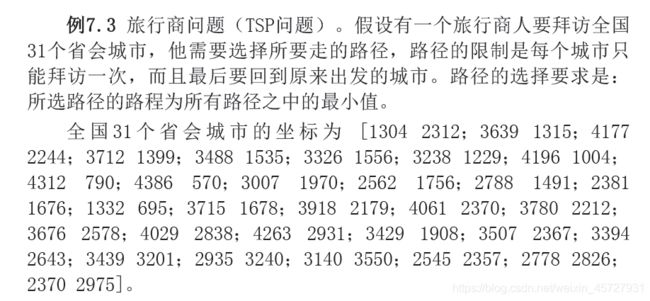
本题并没有要求旅行商的起点在哪儿,不太符合实际情况。实际上,我们更常常会遇到的是解决起点固定的TSP问题,比如无人机巡航等。本题,假设旅行商的起始位置坐标是[2000,2000]。
2. 程序修改思路
本着尽可能动较少代码的原则,我只修改了距离计算函数func3,还有绘制图像的部分。
修改后func3函数如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%计算路线总长度%%%%%%%%%%%%%%%%%%%%%%%%
function len=func3(start,city,n)
len=0;
for i=1:n-1
len=len+sqrt((city(i).x-city(i+1).x)^2+(city(i).y-city(i+1).y)^2);
end
len=len+sqrt((city(1).x-start(1))^2+(city(1).y-start(2))^2);
len=len+sqrt((city(n).x-city(1).x)^2+(city(n).y-city(1).y)^2);
end
主函数部分,给所有的func3函数多输入一个参数start,代表起始点坐标。
主函数部分代码如下:
%%%%%%%%%%%%%%%%%%%%%%模拟退火算法解决TSP问题%%%%%%%%%%%%%%%%%%%%%%%
% 如果将该算法改为固定位置,起始位置为[2000,2000]
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
start=[2000,2000];
C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
3238 1229;4196 1044;4312 790;4386 570;3007 1970;2562 1756;...
2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;...
3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
2370 2975]; %31个省会城市坐标
n=size(C,1); %TSP问题的规模,即城市数目
T=100*n; %初始温度
L=100; %马可夫链长度
K=0.99; %衰减参数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%城市坐标结构体%%%%%%%%%%%%%%%%%%%%%%%%%%
city=struct([]); %结构体变量,类似python中的字典
for i=1:n %city(i)的值为第i座城市的坐标
city(i).x=C(i,1);
city(i).y=C(i,2);
end
l=1; %统计迭代次数
len(l)=func3(start,city,n); %每次迭代后的路线长度
% figure(1);
while T>0.001 %停止迭代温度
%%%%%%%%%%%%%%%%多次迭代扰动,温度降低之前多次实验%%%%%%%%%%%%%%%
for i=1:L
%%%%%%%%%%%%%%%%%%%计算原路线总距离%%%%%%%%%%%%%%%%%%%%%%%%%
len1=func3(start,city,n);
%%%%%%%%%%%%%%%%%%%%%%%%%产生随机扰动%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%随机置换两个不同的城市的坐标%%%%%%%%%%%%%%%%%
q = randi([1,n],1,2); %这是我改的方法
while q(1) == q(2) % q取1到n之间两个不同的数
q = randi([1,n],1,2);
end
tmp_city=city;
tmp=tmp_city(q(1));
tmp_city(q(1))=tmp_city(q(2));
tmp_city(q(2))=tmp;
%%%%%%%%%%%%%%%%%%%%%%%%计算新路线总距离%%%%%%%%%%%%%%%%%%%%
len2=func3(start,tmp_city,n);
%%%%%%%%%%%%%%%%%%新老距离的差值,相当于能量%%%%%%%%%%%%%%%%%
delta_e=len2-len1;
%%%%%%%%%%%%新路线好于旧路线,用新路线代替旧路线%%%%%%%%%%%%%%
if delta_e<0
city=tmp_city;
else
%%%%%%%%%%%%%%%%%%以概率选择是否接受新解%%%%%%%%%%%%%%%%%
if exp(-delta_e/T)>rand()
city=tmp_city;
end
end
end
l=l+1;
%%%%%%%%%%%%%%%%%%%%%%%%%计算新路线距离%%%%%%%%%%%%%%%%%%%%%%%%%%
len(l)=func3(start,city,n);
%%%%%%%%%%%%%%%%%%%%%%%%%%%温度不断下降%%%%%%%%%%%%%%%%%%%%%%%%%%
T=T*K;
% for i=1:n-1
% plot([city(i).x,city(i+1).x],[city(i).y,city(i+1).y],'bo-');
% hold on;
% end
% plot([city(n).x,city(1).x],[city(n).y,city(1).y],'ro-');
% title(['优化最短距离:',num2str(len(l))]);
% hold off;
% pause(0.005);
end
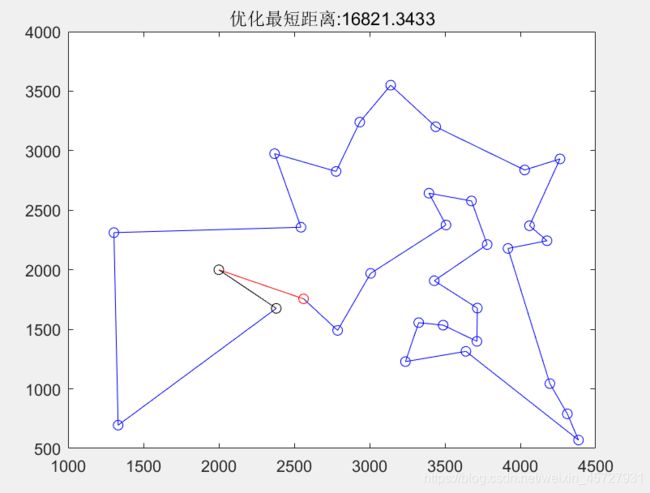
figure(1);
for i=1:n-1
plot([city(i).x,city(i+1).x],[city(i).y,city(i+1).y],'bo-');
hold on;
end
plot([city(n).x,start(1)],[city(n).y,start(2)],'ro-');
plot([city(1).x,start(1)],[city(1).y,start(2)],'ko-');
title(['优化最短距离:',num2str(len(l))])
hold off;
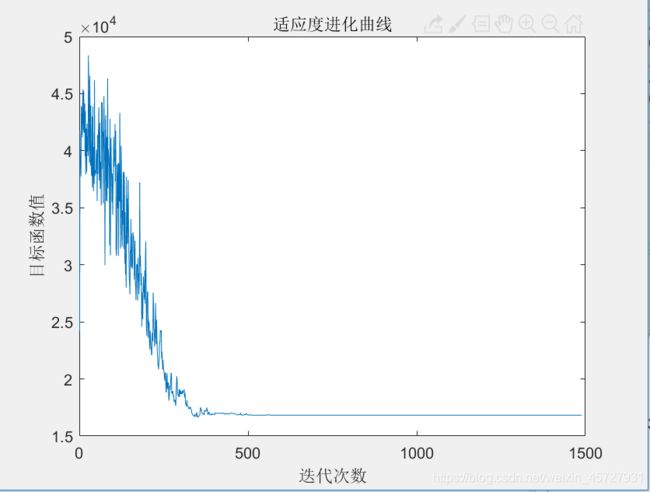
figure(2);
plot(len)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')